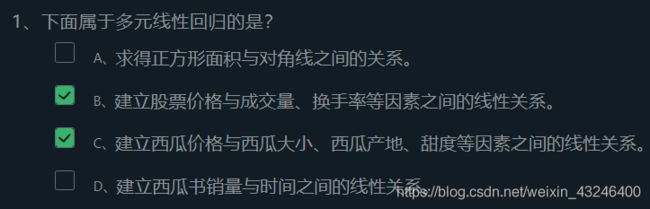
数据挖掘——决策树和K近邻
决策树和K近邻
- 一、线性回归(房价预测)
-
- 第1关:线性回归算法思想
-
- (一)相关知识
-
- 1>简单线性回归
- 2>多元线性回归
- (二)编程要求
- (三)参考答案
- 第2关:动手实现线性回归
-
- (一)相关知识
-
- 1>数据集介绍
- 2>线性回归算法原理
-
- 模型训练流程
- 正规方程解
- 3>线性回归算法流程
- (二)编程要求
- (三)参考代码
- 第3关:衡量线性回归的性能指标
-
- (一)相关知识
-
- 1>前言
- 2>MSE
- 3>RMSE
- 4>MAE
- 5>R-Squared
- (二)编程要求
- (三)参考代码
- 二、决策树
-
- 第1关:决策树算法思想
-
- (一)相关知识
-
- 1>引例
- 2>决策树的相关概念
- (二)编程要求
- (三)参考答案
- 第2关:决策树算法原理
-
- (一)相关知识
-
- 1>信息熵
- 2>条件熵
- 3>信息增益
- (二)编程要求
- (三)参考代码
- 第3关:线性回归算法思想
-
- (一)相关知识
-
- 1>ID3算法
- 2>使用决策树进行预测
- (二)编程要求
- (三)参考代码
- 三、k-近邻
-
- 第1关:knn算法概述
-
- (一)相关知识
-
- 1>knn算法思想
- 2>距离度量
- (二)编程要求
- (三)参考代码
- 第2关:动手实现knn算法
-
- (一)相关知识
-
- 1>数据集介绍
- 2>加权投票
- 3>knn算法流程
- (二)编程要求
- (三)参考代码
一、线性回归(房价预测)
第1关:线性回归算法思想
(一)相关知识
为了完成本关任务,你需要掌握:1.简单线性回归,2.多元线性回归。
1>简单线性回归
在生活中,我们常常能碰到这么一种情况,一个变量会跟着另一个变量的变化而变化,如圆的周长与半径的关系,当圆的半径确定了,那么周长也就确定了。还有一种情况就是,两个变量之间看似存在某种关系,但又没那么确定,如青少年的身高与体重,他们存在一种近似的线性关系:身高/cm = 体重/kg +105。
但是,并不是每个青少年都符合这个公式,只能说每个青少年的身高体重都存在这么一种近似的线性关系。这就是其实就是简单的线性回归,那么,到底什么是线性回归呢?假如我们将青少年的身高和体重值作为坐标,不同人的身高体重就会在平面上构成不同的坐标点,然后用一条直线,尽可能的去拟合这些点,这就是简单的线性回归。

简单的线性回归模型如下:
- y = w x + b y=wx+b y=wx+b
其中x表示特征值(如:体重值),w表示权重,b表示偏置,y表示标签(如:身高值)。
2>多元线性回归
简单线性回归中,一个变量跟另一个变量的变化而变化,但是生活中,还有很多变量,可能由多个变量的变化决定着它的变化,比如房价,影响它的因素可能有:房屋面积、地理位置等等。如果我们要给它们建立出近似的线性关系,这就是多元线性回归,多元线性回归模型如下:
- y = b + w 1 x 1 + w 2 x 2 + . . . + w n x n y=b+w1x1+w2x2+...+wnxn y=b+w1x1+w2x2+...+wnxn
其中xi表示第i个特征值,wi表示第i个特征对应的权重,b表示偏置,y表示标签。
(二)编程要求
根据相关知识,按照要求完成选择题任务,包含单选题和多选题。
(三)参考答案
第2关:动手实现线性回归
(一)相关知识
为了完成本关任务,你需要掌握:1.线性回归算法原理,2.线性回归算法流程。
1>数据集介绍
波士顿房价数据集共有506条波斯顿房价的数据,每条数据包括对指定房屋的13项数值型特征和目标房价组成。我们需要通过数据特征来对目标房价进行预测。
数据集中部分数据与标签如下图所示:

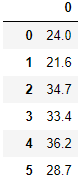
sklearn中已经提供了波士顿房价数据集的相关接口,想要使用该数据集可以使用如下代码:
from sklearn import datasets
#加载波斯顿房价数据集
boston = datasets.load_boston()
#X表示特征,y表示目标房价
x = boston.data
y = boston.target
然后再对数据集进行划分:
from sklearn.model_selection import train_test_split
#划分训练集测试集,所有样本的20%作为测试集
train_feature,test_feature,train_label,test_label = train_test_split(x,y,test_size=0.2,random_state=666)
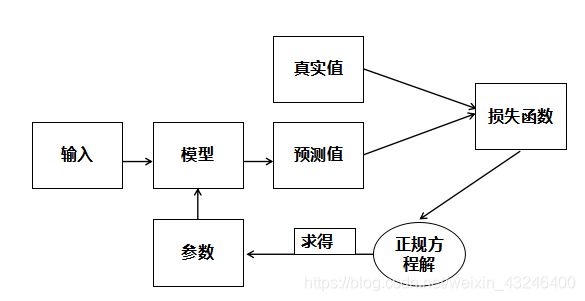
2>线性回归算法原理
模型训练流程
由数据集可以知道,每一个样本有13个特征与目标房价,而我们要做的事就是通过这13个特征来预测房价,我们可以构建一个多元线性回归模型,来对房价进行预测。模型如下:
- y = b + w 1 x 1 + w 2 x 2 + . . . + w n x n y=b+w1x1+w2x2+...+wnxn y=b+w1x1+w2x2+...+wnxn
其中xi表示第i个特征值,wi表示第i个特征对应的权重,b表示偏置,y表示目标房价。
为了方便,我们稍微将模型进行变换:
- y = w 0 x 0 + w 1 x 1 + w 2 x 2 + . . . + w n x n y=w0x0+w1x1+w2x2+...+wnxn y=w0x0+w1x1+w2x2+...+wnxn
其中x0=1。
- Y = θ . X Y=θ.X Y=θ.X
- θ = ( w 0 , w 1 , . . . , w n ) θ=(w0,w1,...,wn) θ=(w0,w1,...,wn)
- X = ( 1 , x 1 , . . . , x n ) X=(1,x1,...,xn) X=(1,x1,...,xn)
而我们的目的就是找出能够正确预测的多元线性回归模型,即找出正确的参数θ。那么如何寻找呢?通常在监督学习里面都会使用这么一个套路,构造一个损失函数,用来衡量真实值与预测值之间的差异,然后将问题转化为最优化损失函数。既然损失函数是用来衡量真实值与预测值之间的差异那么很多人自然而然的想到了用所有真实值与预测值的差的绝对值来表示损失函数。不过带绝对值的函数不容易求导,所以采用MSE(均方误差)作为损失函数,公式如下:
- l o s s = 1 m ∑ i = 1 n ( y i − p i ) 2 loss=\dfrac{1}{m}\displaystyle\sum_{i=1}^n(y^i-p^i)^2 loss=m1i=1∑n(yi−pi)2
其中p表示预测值,y表示真实值,m为样本总个数,i表示第i个样本。最后,我们再使用正规方程解来求得我们所需要的参数。
正规方程解
对线性回归模型,假设训练集中m个训练样本,每个训练样本中有n个特征,可以使用矩阵的表示方法,预测函数可以写为:
- Y = θ X Y=\theta X Y=θX
其损失函数可以表示为
- ( Y − θ X ) T ( Y − θ X ) (Y-\theta X)^T(Y-\theta X) (Y−θX)T(Y−θX)
其中,标签Y为mx1的矩阵,训练特征X为mx(n+1)的矩阵,回归系数θ为(n+1)x1的矩阵,对θ求导,并令其导数等于0,可以得到 X T ( Y − θ X ) = 0 X^T(Y−\theta X)=0 XT(Y−θX)=0。所以,最优解为:
- θ = ( X T X ) − 1 X T Y \theta=(X^TX)^{-1}X^TY θ=(XTX)−1XTY
这个就是正规方程解,我们可以通过最优方程解直接求得我们所需要的参数。
3>线性回归算法流程
我们最终的目的是通过训练出来的线性回归模型对测试集数据进行预测,算法实现流程如下:
1.将x0=1加入训练数据
2.使用正规方程解求得参数
3.将x0=1加入测试数据
4.对测试集数据进行预测
(二)编程要求
根据提示,在编辑器Begin-End处补充Python代码,实现线性回归算法与MSE损失函数计算方法,并利用房价数据对模型进行训练,然后对未知的房价数据进行预测。只需返回预测结果即可,程序内部会检测您的代码,MSE低于30则视为过关。
(三)参考代码
# encoding=utf8
import numpy as np
# mse
def mse_score(y_predict, y_test):
#********* Begin *********#
mse = np.mean((y_predict-y_test)**2)
#********* End *********#
return mse
def lr(train_feature, train_label, test_feature):
'''
input:
train_feature(ndarray):训练样本特征
train_label(ndarray):训练样本标签
test_feature(ndarray):测试样本特征
output:
predict(ndarray):测试样本预测标签
'''
#********* Begin *********#
# 将x0=1加入训练数据
x = np.hstack([np.ones((len(train_feature), 1)), train_feature])
# 使用正规方程解求得参数
theta = np.linalg.inv(x.T@x)@x.T@train_label
# 将x0=1加入测试数据
y = np.hstack([np.ones((len(test_feature), 1)), test_feature])
predict = y@theta
# 求得测试集预测标签
#********* End *********#
return predict
第3关:衡量线性回归的性能指标
(一)相关知识
为了完成本关任务,你需要掌握:
1.均方误差(MSE)
2.均方根误差(RMSE)
3.平均绝对误差(MAE)
4.R-Squared
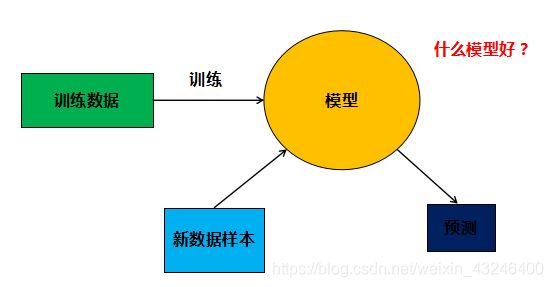
1>前言
大家知道已经,机器学习通常都是将训练集上的数据对模型进行训练,然后再将测试集上的数据给训练好的模型进行预测,最后根据模型性能的好坏选择模型,对于分类问题,大家很容易想到,可以使用正确率来评估模型的性能,那么回归问题可以使用哪些指标用来评估呢?
2>MSE
MSE (Mean Squared Error)叫做均方误差,公式如下:
- 1 m ∑ i = 1 m ( y i − p i ) 2 \dfrac{1}{m}\displaystyle\sum_{i=1}^m(y^i-p^i)^2 m1i=1∑m(yi−pi)2
其中 y i y^i yi表示第i个样本的真实标签, p i p^i pi表示模型对第i个样本的预测标签。线性回归的目的就是让损失函数最小。那么模型训练出来了,我们在测试集上用损失函数来评估模型就行了。
3>RMSE
RMSE(Root Mean Squard Error)均方根误差,公式如下:
- 1 m ∑ i = 1 m ( y i − p i ) 2 \sqrt{\dfrac{1}{m}\displaystyle\sum_{i=1}^m(y^i-p^i)^2} m1i=1∑m(yi−pi)2
RMSE其实就是MSE开个根号。有什么意义呢?其实实质是一样的。只不过用于数据更好的描述。
例如:要做房价预测,每平方是万元,我们预测结果也是万元。那么差值的平方单位应该是千万级别的。那我们不太好描述自己做的模型效果。怎么说呢?我们的模型误差是多少千万?于是干脆就开个根号就好了。我们误差的结果就跟我们数据是一个级别的了,在描述模型的时候就说,我们模型的误差是多少万元。
4>MAE
MAE(平均绝对误差),公式如下:
- 1 m ∑ i = 1 m ∣ y i − p i ∣ \dfrac{1}{m}\displaystyle\sum_{i=1}^m|y^i-p^i| m1i=1∑m∣yi−pi∣
MAE虽然不作为损失函数,确是一个非常直观的评估指标,它表示每个样本的预测标签值与真实标签值的L1距离。
5>R-Squared
上面的几种衡量标准针对不同的模型会有不同的值。比如说预测房价 那么误差单位就是万元。数子可能是3,4,5之类的。那么预测身高就可能是0.1,0.6之类的。没有什么可读性,到底多少才算好呢?不知道,那要根据模型的应用场景来。 看看分类算法的衡量标准就是正确率,而正确率又在0~1之间,最高百分之百。最低0。那么线性回归有没有这样的衡量标准呢?
R-Squared就是这么一个指标,公式如下:
- R 2 = 1 − ∑ i ( p i − y i ) 2 ∑ i ( y m e a n s i − y i ) 2 R^2=1-\dfrac{\displaystyle\sum_{i}(p^i-y^i)^2}{\displaystyle\sum_{i}(y_{means}^i-y^i)^2} R2=1−i∑(ymeansi−yi)2i∑(pi−yi)2
其中 y m e a n s y_{means} ymeans表示所有测试样本标签值的均值。为什么这个指标会有刚刚我们提到的性能呢?我们分析下公式:
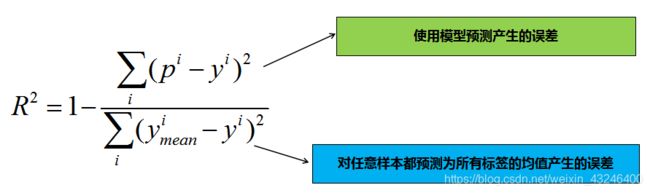
其实分子表示的是模型预测时产生的误差,分母表示的是对任意样本都预测为所有标签均值时产生的误差,由此可知:
- R 2 ≤ 1 R^2≤1 R2≤1,当我们的模型不犯任何错误时,取最大值1。
- 当我们的模型性能跟基模型性能相同时,取0。
- 如果为负数,则说明我们训练出来的模型还不如基准模型,此时,很有可能我们的数据不存在任何线性关系。ps:(基准模型指的随机瞎猜。)
(二)编程要求
根据提示,在编辑器Begin-End处补充代码,用Python实现R-Squared指标,并用实现的R-Squared指标来评估上一关的线性回归模型。只需返回预测结果即可,程序内部会检测您的代码,R-Squared指标高于0.6视为过关。
(三)参考代码
# encoding=utf8
import numpy as np
# mse
def mse_score(y_predict, y_test):
mse = np.mean((y_predict-y_test)**2)
return mse
# r2
def r2_score(y_predict, y_test):
'''
input:y_predict(ndarray):预测值
y_test(ndarray):真实值
output:r2(float):r2值
'''
#********* Begin *********#
r2 = 1-mse_score(y_predict, y_test)/np.var(y_test)
#********* End *********#
return r2
二、决策树
第1关:决策树算法思想
(一)相关知识
为了完成本关任务,你需要掌握决策树的相关基础知识。
1>引例
在炎热的夏天,没有什么比冰镇后的西瓜更能令人感到心旷神怡的了。现在我要去水果店买西瓜,但什么样的西瓜能入我法眼呢?那根据我的个人习惯,在挑西瓜时可能就有这样的脑回路。
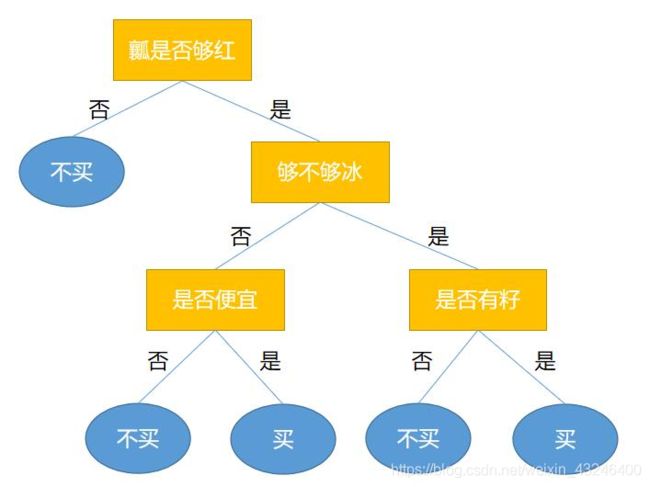
假设现在水果店里有3个西瓜,它们的属性如下:

那么根据我的脑回路我会买1和2号西瓜。
其实我的脑回路可以看成一棵树,并且这颗树能够帮助我对买不买西瓜这件事做决策,所以它就是一棵决策树。
2>决策树的相关概念
决策树是一种可以用于分类与回归的机器学习算法,但主要用于分类。用于分类的决策树是一种描述对实例进行分类的树形结构。决策树由结点和边组成,其中结点分为内部结点和叶子结点,内部结点表示一个特征或者属性,叶子结点表示标签(脑回路图中黄色的是内部结点,蓝色的是叶子结点)。
从代码角度来看,决策树其实可以看成是一堆if-else语句的集合,例如引例中的决策树完全可以看成是如下代码:
if isRed:
if isCold:
if hasSeed:
print("buy")
else:
print("don't buy")
else:
if isCheap:
print("buy")
else:
print("don't buy")
else:
print("don't buy")
因此决策树的一个非常大的优势就是模型的可理解性非常高,甚至可以用来挖掘数据中比较重要的信息。
那么如何构造出一棵好的决策树呢?其实构造决策树时会遵循一个指标,有的是按照信息增益来构建,如ID3算法;有的是信息增益率来构建,如C4.5算法;有的是按照基尼系数来构建的,如CART算法。但不管是使用哪种构建算法,决策树的构建过程通常都是一个递归选择最优特征,并根据特征对训练集进行分割,使得对各个子数据集有一个最好的分类的过程。
这一过程对应着对特征空间的划分,也对应着决策树的构建。一开始,构建决策树的根结点,将所有训练数据都放在根结点。选择一个最优特征,并按照这一特征将训练数据集分割成子集,使得各个子集有一个在当前条件下最好的分类。如果这些子集已经能够被基本正确分类,那么构建叶子结点,并将这些子集分到所对应的叶结点中去;如果还有子集不能被基本正确分类,那么就对这些子集选择新的最优特征,继续对其进行分割,并构建相应的结点。如此递归进行下去,直至所有训练数据子集被基本正确分类,或者没有合适的特征为止。最后每个子集都被分到叶子结点上,即都有了明确的类别。这就构建出了一棵决策树。
(二)编程要求
根据相关知识,按照要求完成选择题任务,包含单选题和多选题。
(三)参考答案
第2关:决策树算法原理
(一)相关知识
为了完成本关任务,你需要掌握:
- 信息熵
- 条件熵
- 信息增益
1>信息熵
信息是个很抽象的概念。人们常常说信息很多,或者信息较少,但却很难说清楚信息到底有多少。比如一本五十万字的中文书到底有多少信息量。
直到1948年,香农提出了“信息熵”的概念,才解决了对信息的量化度量问题。信息熵这个词是香农从热力学中借用过来的。热力学中的热熵是表示分子状态混乱程度的物理量。香农用信息熵的概念来描述信源的不确定度。信源的不确定性越大,信息熵也越大。
从机器学习的角度来看,信息熵表示的是信息量的期望值。如果数据集中的数据需要被分成多个类别,则信息量 I ( x i ) I(x_i) I(xi)的定义如下(其中 x i x_i xi表示多个类别中的第 i i i个类别, p ( x i ) p(x_i) p(xi)数据集中类别为 x i x_i xi的数据在数据集中出现的概率表示):
- I ( x i ) = − l o g 2 p ( x i ) I(x_i)=-log_2p(x_i) I(xi)=−log2p(xi)
由于信息熵是信息量的期望值,所以信息熵H(X)的定义如下(其中n为数据集中类别的数量):
- H ( X ) = − ∑ i = 1 n p ( x i ) l o g 2 p ( x i ) H(X)=-\displaystyle\sum_{i=1}^np(x_i)log_2p(x_i) H(X)=−i=1∑np(xi)log2p(xi)
从这个公式也可以看出,如果概率是0或者是1的时候,熵就是0。(因为这种情况下随机变量的不确定性是最低的),那如果概率是0.5也就是五五开的时候,此时熵达到最大,也就是1。(就像扔硬币,你永远都猜不透你下次扔到的是正面还是反面,所以它的不确定性非常高)。所以呢,熵越大,不确定性就越高。
2>条件熵
在实际的场景中,我们可能需要研究数据集中某个特征等于某个值时的信息熵等于多少,这个时候就需要用到条件熵。条件熵H(Y|X)表示特征X为某个值的条件下,类别为Y的熵。条件熵的计算公式如下:
- H ( Y ∣ X ) = ∑ i = 1 n p ( x i ) H ( Y ∣ X = x i ) H(Y|X)=\displaystyle\sum_{i=1}^np(x_i)H(Y|X=x_i) H(Y∣X)=i=1∑np(xi)H(Y∣X=xi)
当然条件熵的一个性质也熵的性质一样,概率越确定,条件熵就越小,概率越五五开,条件熵就越大。
3>信息增益
现在已经知道了什么是熵,什么是条件熵。接下来就可以看看什么是信息增益了。所谓的信息增益就是表示我已知条件X后能得到信息Y的不确定性的减少程度。
就好比,我在玩读心术。你心里想一件东西,我来猜。我已开始什么都没问你,我要猜的话,肯定是瞎猜。这个时候我的熵就非常高。然后我接下来我会去试着问你是非题,当我问了是非题之后,我就能减小猜测你心中想到的东西的范围,这样其实就是减小了我的熵。那么我熵的减小程度就是我的信息增益。
所以信息增益如果套上机器学习的话就是,如果把特征A对训练集D的信息增益记为g(D, A)的话,那么g(D, A)的计算公式就是:
- g ( D , A ) = H ( D ) − H ( D , A ) g(D,A)=H(D)-H(D,A) g(D,A)=H(D)−H(D,A)
为了更好的解释熵,条件熵,信息增益的计算过程,下面通过示例来描述。假设我现在有这一个数据集,第一列是编号,第二列是性别,第三列是活跃度,第四列是客户是否流失的标签(0:表示未流失,1:表示流失)。
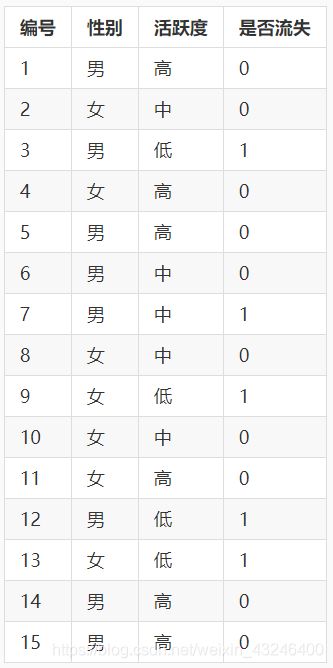
假如要算性别和活跃度这两个特征的信息增益的话,首先要先算总的熵和条件熵。总的熵其实非常好算,就是把标签作为随机变量X。上表中标签只有两种(0和1)因此随机变量X的取值只有0或者1。所以要计算熵就需要先分别计算标签为0的概率和标签为1的概率。从表中能看出标签为0的数据有10条,所以标签为0的概率等于2/3。标签为1的概率为1/3。所以熵为:
- −(1/3)∗log(1/3)−(2/3)∗log(2/3)=0.9182
接下来就是条件熵的计算,以性别为男的熵为例。表格中性别为男的数据有8条,这8条数据中有3条数据的标签为1,有5条数据的标签为0。所以根据条件熵的计算公式能够得出该条件熵为:
- −(3/8)∗log(3/8)−(5/8)∗log(5/8)=0.9543
根据上述的计算方法可知,总熵为:
- −(5/15)∗log(5/15)−(10/15)∗log(10/15)=0.9182
性别为男的熵为:
- −(3/8)∗log(3/8)−(5/8)∗log(5/8)=0.9543
性别为女的熵为:
- −(2/7)∗log(2/7)−(5/7)∗log(5/7)=0.8631
活跃度为低的熵为:
- −(4/4)∗log(4/4)−0=0
活跃度为中的熵为:
- −(1/5)∗log(1/5)−(4/5)∗log(4/5)=0.7219
活跃度为高的熵为:
- −0−(6/6)∗log(6/6)=0
现在有了总的熵和条件熵之后就能算出性别和活跃度这两个特征的信息增益了。
**性别的信息增益=总的熵-(8/15)性别为男的熵-(7/15)性别为女的熵=0.0064
活跃度的信息增益=总的熵-(6/15)活跃度为高的熵-(5/15)
活跃度为中的熵-(4/15)*活跃度为低的熵=0.6776
那信息增益算出来之后有什么意义呢?回到读心术的问题,为了我能更加准确的猜出你心中所想,我肯定是问的问题越好就能猜得越准!换句话来说我肯定是要想出一个信息增益最大(减少不确定性程度最高)的问题来问你。其实ID3算法也是这么想的。ID3算法的思想是从训练集D中计算每个特征的信息增益,然后看哪个最大就选哪个作为当前结点。然后继续重复刚刚的步骤来构建决策树。
(二)编程要求
根据提示,在右侧编辑器Begin-End处补充代码,完成calcInfoGain函数实现计算信息增益。
calcInfoGain函数中的参数:
- feature:测试用例中字典里的feature,类型为ndarray
- label:测试用例中字典里的label,类型为ndarray
- index:测试用例中字典里的index,即feature部分特征列的索引。该索引指的是feature中第几个特征,如index:0表示使用第一个特征来计算信息增益。
提示:
计算log可以使用NumPy中的log2函数
(三)参考代码
import numpy as np
def calcInfoGain(feature, label, index):
'''
计算信息增益
:param feature:测试用例中字典里的feature,类型为ndarray
:param label:测试用例中字典里的label,类型为ndarray
:param index:测试用例中字典里的index,即feature部分特征列的索引。该索引指的是feature中第几个特征,如index:0表示使用第一个特征来计算信息增益。
:return:信息增益,类型float
'''
#*********** Begin ***********#
# 计算熵
def calcInfoEntropy(feature, label):
'''
计算信息熵
:param feature:数据集中的特征,类型为ndarray
:param label:数据集中的标签,类型为ndarray
:return:信息熵,类型float
'''
label_set = set(label)
result = 0
for l in label_set:
count = 0
for j in range(len(label)):
if label[j] == l:
count += 1
# 计算标签在数据集中出现的概率
p = count / len(label)
# 计算熵
result -= p * np.log2(p)
return result
# 计算条件熵
def calcHDA(feature, label, index, value):
'''
计算信息熵
:param feature:数据集中的特征,类型为ndarray
:param label:数据集中的标签,类型为ndarray
:param index:需要使用的特征列索引,类型为int
:param value:index所表示的特征列中需要考察的特征值,类型为int
:return:信息熵,类型float
'''
count = 0
# sub_feature和sub_label表示根据特征列和特征值分割出的子数据集中的特征和标签
sub_feature = []
sub_label = []
for i in range(len(feature)):
if feature[i][index] == value:
count += 1
sub_feature.append(feature[i])
sub_label.append(label[i])
pHA = count / len(feature)
e = calcInfoEntropy(sub_feature, sub_label)
return pHA * e
base_e = calcInfoEntropy(feature, label)
f = np.array(feature)
# 得到指定特征列的值的集合
f_set = set(f[:, index])
sum_HDA = 0
# 计算条件熵
for value in f_set:
sum_HDA += calcHDA(feature, label, index, value)
# 计算信息增益
return base_e - sum_HDA
#*********** End *************#
第3关:线性回归算法思想
(一)相关知识
为了完成本关任务,你需要掌握:
- ID3算法构造决策树的流程
- 如何使用构造好的决策树进行预测
1>ID3算法
ID3算法其实就是依据特征的信息增益来构建树的。其大致步骤就是从根结点开始,对结点计算所有可能的特征的信息增益,然后选择信息增益最大的特征作为结点的特征,由该特征的不同取值建立子结点,然后对子结点递归执行上述的步骤直到信息增益很小或者没有特征可以继续选择为止。
因此,ID3算法伪代码如下:
#假设数据集为D,标签集为A,需要构造的决策树为tree
def ID3(D, A):
if D中所有的标签都相同:
return 标签
if 样本中只有一个特征或者所有样本的特征都一样:
对D中所有的标签进行计数
return 计数最高的标签
计算所有特征的信息增益
选出增益最大的特征作为最佳特征(best_feature)
将best_feature作为tree的根结点
得到best_feature在数据集中所有出现过的值的集合(value_set)
for value in value_set:
从D中筛选出best_feature=value的子数据集(sub_feature)
从A中筛选出best_feature=value的子标签集(sub_label)
#递归构造tree
tree[best_feature][value] = ID3(sub_feature, sub_label)
return tree
2>使用决策树进行预测
决策树的预测思想非常简单,假设现在已经构建出了一棵用来决策是否买西瓜的决策树。
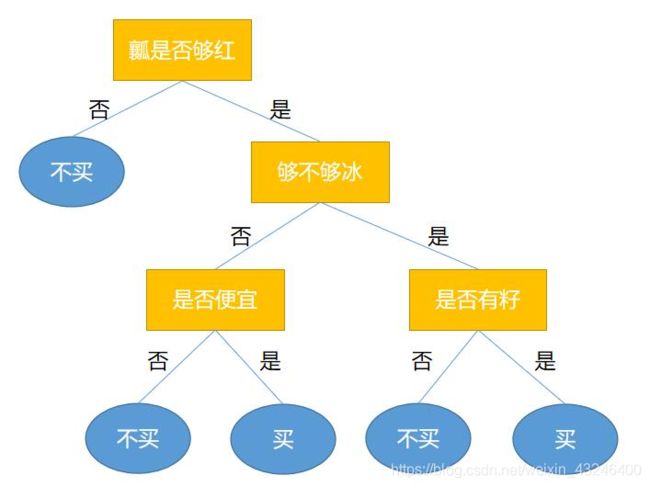
并假设现在在水果店里有这样一个西瓜,其属性如下:

那买不买这个西瓜呢?只需把西瓜的属性代入决策树即可。决策树的根结点是瓤是否够红,所以就看西瓜的属性,经查看发现够红,因此接下来就看够不够冰。而西瓜不够冰,那么看是否便宜。发现西瓜是便宜的,所以这个西瓜是可以买的。
因此使用决策树进行预测的伪代码也比较简单,伪代码如下:
#tree表示决策树,feature表示测试数据
def predict(tree, feature):
if tree是叶子结点:
return tree
根据feature中的特征值走入tree中对应的分支
if 分支依然是课树:
result = predict(分支, feature)
return result
(二)编程要求
填写fit(self, feature, label)函数,实现ID3算法,要求决策树保存在self.tree中。其中:
feature:训练集数据,类型为ndarray,数值全为整数label:训练集标签,类型为ndarray,数值全为整数
填写predict(self, feature)函数,实现预测功能,并将标签返回,其中:
feature:测试集数据,类型为ndarray,数值全为整数。(PS:feature中有多条数据)
只需完成fit与predict函数即可,程序内部会调用您所完成的fit函数构建模型并调用predict函数来对数据进行预测。预测的准确率高于0.92视为过关。(PS:若self.tree is None则会打印决策树构建失败)
(三)参考代码
import numpy as np
# 计算熵
def calcInfoEntropy(label):
'''
input:
label(narray):样本标签
output:
InfoEntropy(float):熵
'''
sv = {}
for v in label:
if v in sv:
sv[v] += 1
else:
sv[v] = 1
InfoEntropy = 0
for v in sv:
InfoEntropy -= (sv[v]/len(label)) * np.log2(sv[v]/len(label))
return InfoEntropy
# 计算条件熵
def calcHDA(feature, label, index, value):
'''
input:
feature(ndarray):样本特征
label(ndarray):样本标签
index(int):需要使用的特征列索引
value(int):index所表示的特征列中需要考察的特征值
output:
HDA(float):信息熵
'''
count = 0
# sub_feature和sub_label表示根据特征列和特征值分割出的子数据集中的特征和标签
sub_feature = feature[feature[:, index] == value, :]
sub_label = label[feature[:, index] == value]
count = feature[feature[:, index] == value, :].shape[0]
pHA = count / len(feature)
e = calcInfoEntropy(sub_label)
HDA = pHA * e
return HDA
# 计算信息增益
def calcInfoGain(feature, label, index):
'''
input:
feature(ndarry):测试用例中字典里的feature
label(ndarray):测试用例中字典里的label
index(int):测试用例中字典里的index,即feature部分特征列的索引。该索引指的是feature中第几个特征,如index:0表示使用第一个特征来计算信息增益。
output:
InfoGain(float):信息增益
'''
base_e = calcInfoEntropy(label)
f = np.array(feature)
# 得到指定特征列的值的集合
f_set = set(f[:, index])
sum_HDA = 0
# 计算条件熵
for value in f_set:
sum_HDA += calcHDA(feature, label, index, value)
# 计算信息增益
InfoGain = base_e - sum_HDA
return InfoGain
# 获得信息增益最高的特征
def getBestFeature(feature, label):
'''
input:
feature(ndarray):样本特征
label(ndarray):样本标签
output:
best_feature(int):信息增益最高的特征
'''
t = ""
maxn = -100
for i in range(feature.shape[1]):
tmp = calcInfoGain(feature, label, i)
if tmp > maxn:
t = i
maxn = tmp
best_feature = t
return best_feature
# 创建决策树
def createTree(feature, label):
'''
input:
feature(ndarray):训练样本特征
label(ndarray):训练样本标签
output:
tree(dict):决策树模型
'''
# 样本里都是同一个label没必要继续分叉了
if len(set(list(label))) == 1:
return label[0]
# 样本s中只有一个特征或者所有样本的特征都一样的话就看哪个label的票数高
equ = False
tmps = []
for i in feature:
tmps.append(str(i))
tmps = np.array(tmps)
if feature[0].shape[0] == 1 or tmps[tmps == tmps[0]].shape == tmps.shape:
return np.where(np.bincount(label) == max(np.bincount(label)))[0]
# 根据信息增益拿到特征的索引
bf = getBestFeature(feature, label)
tree = {bf: {}}
# 拿到bestfeature的所有特征值
fvalue = list(set(feature[:, bf]))
# 构建对应特征值的子样本集sub_feature, sub_label
for v in fvalue:
sub_feature = feature[feature[:, bf] == v, :]
sub_label = label[feature[:, bf] == v]
# 递归
tree[bf][v] = createTree(sub_feature, sub_label)
return tree
def pred(tree, feature):
if not isinstance(tree, dict):
return tree
f = list(tree.keys())[0]
return pred(tree[f][feature[f]], feature)
# 决策树分类
def dt_clf(train_feature, train_label, test_feature):
'''
input:
train_feature(ndarray):训练样本特征
train_label(ndarray):训练样本标签
test_feature(ndarray):测试样本特征
output:
predict(ndarray):测试样本预测标签
'''
# 创建决策树
tree = createTree(train_feature, train_label)
# 根据tree与特征进行分类
predict = []
for f in test_feature:
predict.append(pred(tree, f))
return predict
三、k-近邻
第1关:knn算法概述
(一)相关知识
为了完成本关任务,你需要掌握:1.knn算法思想,2.距离度量。
1>knn算法思想
k-近邻(k-nearest neighbor ,knn)是一种分类与回归的方法。我们这里只讨论用来分类的knn。所谓k最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最近的k个邻居来代表。
knn算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。knn方法在类别决策时,只与极少量的相邻样本有关。
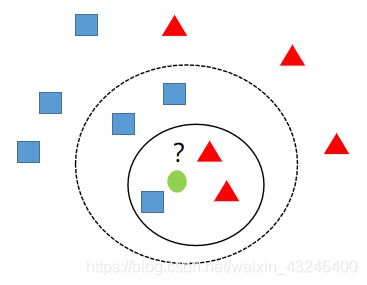
如上图,当k=3时离绿色的圆最近的三个样本中,有两个红色的三角形,一个蓝色的正方形,则此时绿色的圆应该分为红色的三角形这一类。而当k=5时,离绿色的圆最近的五个样本中,有两个红色的三角形,三个蓝色的正方形,则此时绿色的圆应该分为蓝色的正方形这一类。
2>距离度量
我们已经知道,如何判别一个样本属于哪个类型,主要是看离它最近的几个样本中哪个类型的数量最多,则该样本属于数量最多的类型。这里,有一个问题:何为最近?
关于何为最近,大家应该自然而然就会想到可以用两个样本之间的距离大小来衡量,我们常用的有两种距离:
- 欧氏距离:欧氏距离是最容易直观理解的距离度量方法,我们小学、初中和高中接触到的两个点在空间中的距离一般都是指欧氏距离。
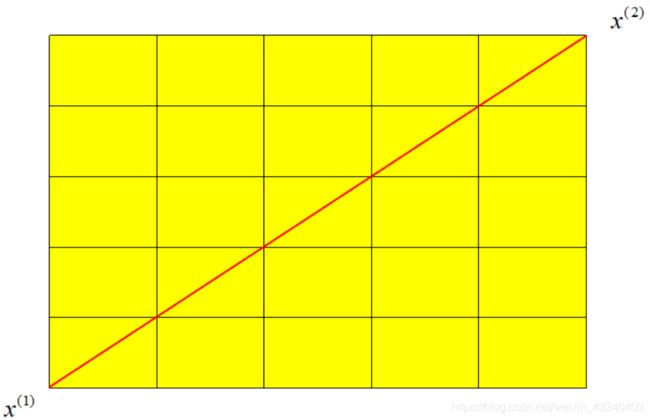
二维平面上欧式距离计算公式:
d 12 = ( x 1 ( 1 ) − x 1 ( 2 ) ) 2 + ( x 2 ( 1 ) − x 2 ( 2 ) ) 2 d_{12}=\sqrt{(x_1^{(1)}-x_1^{(2)})^2+(x_2^{(1)}-x_2^{(2)})^2} d12=(x1(1)−x1(2))2+(x2(1)−x2(2))2
n维平面上欧氏距离计算公式:
d 12 = ∑ i = 1 n ( x i ( 1 ) − x i ( 2 ) ) 2 d_{12}=\sqrt{\displaystyle\sum_{i=1}^n(x_i^{(1)}-x_i^{(2)})^2} d12=i=1∑n(xi(1)−xi(2))2 - 曼哈顿距离:顾名思义,在曼哈顿街区要从一个十字路口开车到另一个十字路口,驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”。

二维平面上曼哈顿距离计算公式:
d 12 = ∣ x 1 ( 1 ) − x 1 ( 2 ) ∣ + ∣ x 2 ( 1 ) − x 2 ( 2 ) ∣ d_{12}=|x_1^{(1)}-x_1^{(2)}|+|x_2^{(1)}-x_2^{(2)}| d12=∣x1(1)−x1(2)∣+∣x2(1)−x2(2)∣
n维平面上曼哈顿计算公式:
d 12 = ∑ i = 1 n ∣ x i ( 1 ) − x i ( 2 ) ∣ d_{12}=\displaystyle\sum_{i=1}^n|x_i^{(1)}-x_i^{(2)}| d12=i=1∑n∣xi(1)−xi(2)∣
其中,上标圆括号内数字代表第几个样本,下标数字代表样本的第几个特征。
(二)编程要求
根据提示,在编辑器Begin-End处补充代码,实现topK方法。程序会调用你实现的方法,找出目标样本最近的k个样本的标签。如目标样本最近的5个样本为0,0,1,1,1则返回列表[0,0,1,1,1]。若返回结果与真实结果一致则视为通关。
(三)参考代码
# encoding=utf8
import numpy as np
def topK(i, k, x, y):
'''
input:
i(int):第i个样本
k(int):最近邻样本个数
x(ndarray):数据特征
y(ndarray):数据标签
output:
topK(list):样本i的最近k个样本标签
'''
#*********Begin*********#
topK = [1, 1, 1, 1, 1]
# 计算样本到所有样本的距离
# dis = []
# topK = []
# length = len(x)
# s = 0
# for i in range(length):
# for s in range(1, length-s):
# dis.append(np.linalg.norm(x[i]-x[i+s]))
# # 除样本本身外的最近的k个样本的索引
# Lst = dis[:] # 对列表进行浅复制,避免后面更改原列表数据
# index_k = []
# for i in range(k):
# index_i = Lst.index(max(Lst)) # 得到列表的最da值,并得到该最da值的索引
# index_k.append(index_i) # 记录最da值索引
# Lst[index_i] = -9999 # 将遍历过的列表最da值改为0,下次不再选择
# for i in index_k:
# topK.append(y[i])
# # 除样本本身外的最近的k个样本的标签
#*********End*********#
return topK
第2关:动手实现knn算法
(一)相关知识
为了完成本关任务,你需要掌握:1.加权投票,2.knn算法流程。
1>数据集介绍
手写数字数据集一共有1797个样本,每个样本有64个特征。每个特征的值为0-255之间的像素,我们的任务就是根据这64个特征值识别出该数字属于0-9十个类别中的哪一个。
我们可以使用sklearn直接对数据进行加载,代码如下:
from sklearn.datasets import load_digits
#加载手写数字数据集
digits = load_digits()
#获取数据特征与标签
x,y = digits .data,digits .target
当然,每一个样本就是一个数字,我们可以把它还原为8x8的大小进行查看:
import matplotlib.pyplot as plt
img = x[0].reshape(8,8)
plt.imshow(img)
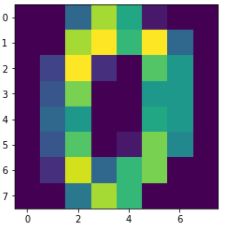
然后我们划分出训练集与测试集,训练集用来训练模型,测试集用来检测模型性能。代码如下:
from sklearn.model_selection import train_test_split
#划分训练集测试集,其中测试集样本数为整个数据集的20%
train_feature,test_feature,train_label,test_label = train_test_split(x,y,test_size=0.2,random_state=666)
2>加权投票
通过上一关,我们已经知道如何找出最近的k个样本,但是,现在还有一个问题要我们来解决:如果有两个类型的样本数一样且最多,那么最终该样本应该属于哪个类型?
其实,knn算法最后决定样本属于哪个类别,其实好比就是在投票,哪个类别票数多,则该样本属于哪个类别。而如果出现票数相同的情况,我们可以给每一票加上一个权重,用来表示每一票的重要性,这样就可以解决票数相同的问题了。很明显,距离越近的样本所投的一票应该越重要,此时我们可以将距离的倒数作为权重赋予每一票。

如上图,虽然蓝色正方形与红色三角形数量一样,但是根据加权投票的规则,绿色的圆应该属于蓝色正方形这个类别。
3>knn算法流程
knn算法不需要训练模型,只是根据离样本最近的几个样本类型来判别该样本类型,所以流程非常简单:
1.计算出新样本与每一个样本的距离
2.找出距离最近的k个样本
3.根据加权投票规则得到新样本的类别
(二)编程要求
根据提示,在编辑器Begin-End处补充代码,实现knn算法。程序会调用你的实现的方法对手写数字进行识别,正确率大于0.95则视为通关。
(三)参考代码
# encoding=utf8
import numpy as np
def knn_clf(k, train_feature, train_label, test_feature):
'''
input:
k(int):最近邻样本个数
train_feature(ndarray):训练样本特征
train_label(ndarray):训练样本标签
test_feature(ndarray):测试样本特征
output:
predict(ndarray):测试样本预测标签
'''
#*********Begin*********#
def topK(i, k, sam, x, y):
'''
input:
i(int):第i个样本
k(int):最近邻样本个数
x(ndarray):数据特征
y(ndarray):数据标签
output:
topK(list):样本i的最近k个样本标签
'''
# 计算样本到所有样本的距离
dis = []
for s in range(len(x)):
tmp = sam - x[s]
S = 0
for t in tmp:
S += abs(t)
dis.append([S, s])
# 除样本本身外的最近的k个样本的索引
dis = sorted(dis, key=lambda x: x[0])
# 除样本本身外的最近的k个样本的标签
for a in range(k):
dis[a].append(y[dis[a][1]])
'''
output:
dis中每一项是个三元组,具体为:(样本的距离,样本的索引,样本的标签)
'''
return dis[:k]
predict = []
# 对测试集每一个样本进行遍历
for ti in range(len(test_feature)):
# 测试集第i个样本到训练集每一个样本的距离
dis = topK(ti, k, test_feature[ti], train_feature, train_label)
# 初始化进行投票的字典,字典的键为标签,值为投票分数
dic = {}
for d in dis:
# 进行投票
if d[2] not in dic:
# 如果标签不在字典中则将标签加入字典的键,同时计入相应的分数
dic[d[2]] = 1.0/d[0]
else:
# 如果标签在字典的键中则投票计分
dic[d[2]] += 1.0/d[0]
# 计入投票评分最高的类别最为预测结果
predict.append(
sorted(list(dic.items()), key=lambda x: x[1], reverse=True)[0][0])
#*********End*********#
return predict
原文链接:https://blog.csdn.net/weixin_43246400/article/details/116134655
@date: 2021.04.25
@author: zkinglin
(完)