Q Learnin 关于机器人在巡检与点检中的最佳路线获得

本文简单介绍了在工厂生产环境中，使用巡检与点检机器人的时候，机器人的路线选择问题。通过使用Q Learnin 算法中的，随机，奖励，行为等状态来进行路线训练，来获得每次任务的最佳移动路线。

1 业务场景

工厂环境：

假设我们在一个有很多不同工艺流程的工厂车间中，智能机器人（检测智能体）帮助工人们巡检，点检不同工艺中的设备运行情况。工厂中通过这些工艺流程来运送，组装，生产，维修等来维持工厂的正常运转。下面这些工艺流程中使用的设备位于工厂的不同位置。

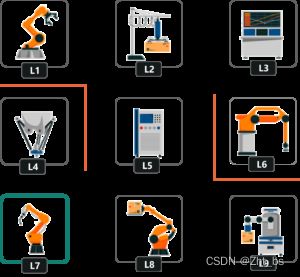
检测智能机器人出现在对应工序中设备的位置进行编码，我们通过数字的映射就知道检测智能机器人所在设备的位置。

机器人运动：

在不同生产工艺中检测智能机器人要移动到工艺中使用到的设备旁边进行状态检测与维修帮助，工艺中会使用到不同设备，检测智能机器人要移动到下一个设备，这个时候机器人会出现多种选择。例如机器人位于 L2 位置，它可以移动到的位置是 L5、L1 和 L3。

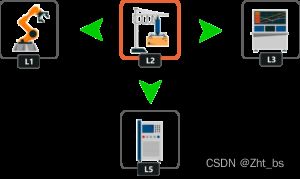
路线选择奖励：

我们对巡检机器人直接从一种位置的状态进入到另一个位置的状态将进行奖励。例如 从 L2到达 L5，或者巡检机器人做出其它任何选择，无论哪种情况都奖励值加+ 1进行奖励。

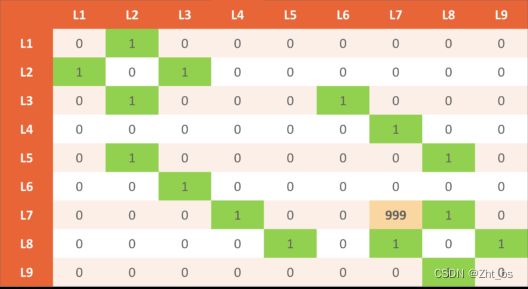
奖励表

例如工人李师傅喜欢在A工艺中优先检测设备L7位置，我们将把这个事实纳入我们的奖励表中。因此，我们将在 (L7, L7) 位置分配一个非常大的奖励数字（为 999）。

2 贝尔曼方程

现在假设巡检机器人需要从 A 点到 B 点，它会选择产生奖励的路径。我们在足迹方面提供奖励，巡检机器人会按照奖励的路径进行运动。

如果巡检机器人面前出现多条路径，它会选择哪条路径进行运动呢？巡检机器人它不会做出任何决定，这主要是因为它没有智慧，它不能像人一样做出判断。这个时候就需贝尔曼方程出现了。

V(s) = max(R(s,a) + V(s’))

参数：

• s = 特定状态
• a = 行动
• s′ = 机器人从 s 进入的状态
• = 折扣系数
• R(s, a) = 一个奖励函数，它接受状态 (s) 和动作 (a) 并输出奖励值
• V(s) = 处于特定状态的值

现在每个格子的奖励值都设置为 reward 1，那我们怎么样区分不同格子的奖励呢？这个时候我们会使用到折扣因子。假设折扣因子为 0.9，并一一填充到所有块中。

3 马尔可夫决策过程

例如巡检机器人在橙色方块上，需要到达目的地。巡检机器人是不知道选择哪条路是正确的方向。

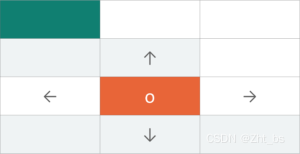
所以我们需要使用到部分随机，部分算法控制的决策过程。为什么要有部分随机的决策，因为现场情况很复杂很多时候原本通顺的道路会被临时出现的杂物，人员堵住无法通过，需要改变路径。算法控制是仍然是机器人的决定，它构成了马尔可夫决策过程的基础。

马尔可夫决策过程（MDP）是一个离散时间随机控制过程。它提供了一个数学框架，用于在结果部分随机且部分受决策者控制的情况下对决策进行建模。

我们将使用我们原来的贝尔曼方程并对其进行修改。巡检机器人不知道下一个状态 s’。我们通过方程式计算得到转弯的所有可能性。

V(s) = max(R(s, a) + V(s’))

*V(s) = max(R(s, a) + *Σ s’ P(s, a, s’)* V(s’))

P(s,a,s’) :从状态移动的概率到_s’与动作a

Σ s’ P(s,a,s’) V(s’) : 机器人的随机性期望

V(s) = max(R(s, a) + ((0.8V(向上)) + (0.1V(向下) + …))

现在样我们真正的使用Q Learning来帮助机器人判断一下步移动到什么位置吧，而不是它可能移动到那个位置。

我们将得到机器人要移动到某个状态 s’ 的动作值。更新贝尔曼方程，我们将删除这个格子中的最大分值。

Q(s, a) = (R(s, a) + Σ s’ P(s, a, s’)V(s’))

在这个移动决策中，我们可以假设 V(s) 是 Q(s, a) 的所有可能值中的最大值。所以让我们用 Q() 的函数替换 v(s’)。

**Q(s, a) = (R(s, a) + *Σ s’ P(s, a, s’)*最大 Q(s’, a’))

我们离最终的 Q Learning 学习就差一步了。我们在引入时间差来计算关于环境随时间变化的 Q 值。

TD(s, a) = (R(s, a) + Σ s’ P(s, a, s’)最大 Q(s’, a’)) – Q(s, a)

我们用相同的公式重新计算新的 Q(s, a) 并从中减去先前已知的 Q(s, a)。因此公式变为：

Q t (s, a) = Q t-1 (s, a) + α TD t (s, a)

**Q t (s, a) =**当前 Q 值

**Q t-1 (s, a) =**前一个 Q 值

Q t (s, a) = Q t-1 (s, a) + α (R(s, a) + max Q(s’, a’) – Q t-1 (s, a))

4 代码实现

第 1 步：导入、参数、状态、动作和奖励

import numpy as np
gamma = 0.75 # 折扣系数
alpha = 0.9 # 学习率
location_to_state = {
    'L1' : 0,
    'L2' : 1,
    'L3' : 2,
    'L4' : 3,
    'L5' : 4,
    'L6' : 5,
    'L7' : 6,
    'L8' : 7,
    'L9' : 8
}
//工序中检测设备
actions = [0,1,2,3,4,5,6,7,8]
//某个工序设备地图奖励初始值
rewards = np.array([[0,1,0,0,0,0,0,0,0],
              [1,0,1,0,0,0,0,0,0],
              [0,1,0,0,0,1,0,0,0],
              [0,0,0,0,0,0,1,0,0],
              [0,1,0,0,0,0,0,1,0],
              [0,0,1,0,0,0,0,0,0],
              [0,0,0,1,0,0,0,1,0],
              [0,0,0,0,1,0,1,0,1],
              [0,0,0,0,0,0,0,1,0]])

state_to_location = dict((state,location) for location,state in location_to_state.items())

第 2 步：获得最佳路线

def getOptimalRoute(sl,el):
    rewards_new = np.copy(rewards)
    ending_state = location_to_state[el]
    rewards_new[ending_state,ending_state] = 999
    Q = np.array(np.zeros([9,9]))
 
    # Q-Learning 训练1000次
    for i in range(1000):
        # 随机状态
        current_state = np.random.randint(0,9)
        playable_actions = []
        # 遍历奖励矩阵
        for j in range(9):
            if rewards_new[current_state,j] > 0:
                playable_actions.append(j)
        # 选择一个随机动作，进入下一个状态
        next_state = np.random.choice(playable_actions)
        # 计算时间差异
        TD = rewards_new[current_state,next_state] + gamma * Q[next_state, np.argmax(Q[next_state,])] - Q[current_state,next_state]
        # 使用贝尔曼方程更新 Q 值
        Q[current_state,next_state] += alpha * TD
        
    # 用起始位置初始化最优路线
    route = [sl]
    #用起始位置初始化 next_location
    next_location = sl
    # 位置状态设置
    while(next_location != el):
        # 获取起始状态
        starting_state = location_to_state[sl]
        # 获取与起始状态有关的最高 Q 值
        next_state = np.argmax(Q[starting_state,])
        # 得到了下一个状态的索引
        next_location = state_to_location[next_state]
        route.append(next_location)
        # 更新下一次迭代的起始位置
        start_location = next_location
 
return route
print(getOptimalRoute('L1', 'L9'))