pytorch损失函数解析
目录
- nn.L1Loss:
- nn.NLLLoss:
- nn.CrossEntropyLoss
- nn.MSELoss
- nn.BCELoss:
nn.L1Loss:
这个比较简单,没有太多好说的,就是两者做差取绝对值,然后求和取平均。
输入x和目标y之间差的绝对值,要求 x 和 y 的维度要一样(可以是向量或者矩阵),得到的 loss 维度也是对应一样的。
loss(x,y)=1/n ∑ \sum ∑ |x_i-y_i|
nn.NLLLoss:
nn.NLLLoss是负的似然对数损失,但Pytorch的实现就是把对应target上的数取出来再加个负号,要在CrossEntropy中结合LogSoftmax来用。
让我们用代码实现一下,来深入理解上面黑色加粗字的含义:
import torch
import torch.nn as nn
num=torch.Tensor([[1,2,3]])
a=torch.Tensor([0]).long()
b=torch.Tensor([1]).long()
c=torch.Tensor([2]).long()
nll=nn.NLLLoss()
print(nll(num,a))
print(nll(num,b))
print(nll(num,c))
#输出
#tensor(-1.)
#tensor(-2.)
#tensor(-3.)
如果是多行数据,则取平均值,reduction=‘none’ 表示显示全部 loss而不是取平均值:
import torch
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(2019)
output = torch.randn(2, 3) # 网路输出
target = torch.ones(2, dtype=torch.long).random_(3) # 真实标签
print(output)
print(target)
# 直接调用
loss = F.nll_loss(output, target)
print(loss)
# 实例化类
criterion = nn.NLLLoss(reduction='none')
loss = criterion(output, target)
print(loss)
"""
tensor([[-0.1187, 0.2110, 0.7463],
[-0.6136, -0.1186, 1.5565]])
tensor([2, 0])
tensor(-0.0664)
tensor([-0.7463, 0.6136])
"""
另外,既然要讲nn.NLLLOSS,那么须得先讲一下logSoftmax。
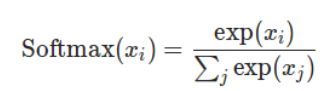
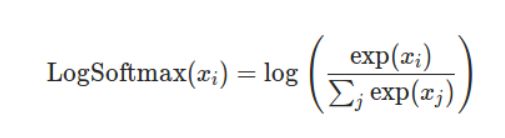
import torch
import torch.nn as nn
a=torch.Tensor([1,2,3])
b=nn.Softmax()(a)
c=nn.LogSoftmax()(a)
print(b)
print(c)
#输出
#tensor([0.0900, 0.2447, 0.6652])
#tensor([-2.4076, -1.4076, -0.4076])
nn.CrossEntropyLoss
这是交叉熵损失函数,通常用于分类问题。有关交叉熵的介绍,我要引用某乎的一篇文章的内容:
什么是交叉熵?
交叉熵主要是用来判定实际的输出与期望的输出的接近程度,为什么这么说呢,举个例子:在做分类的训练的时候,如果一个样本属于第K类,那么这个类别所对应的的输出节点的输出值应该为1,而其他节点的输出都为0,即[0,0,1,0,….0,0],这个数组也就是样本的Label,是神经网络最期望的输出结果。也就是说用它来衡量网络的输出与标签的差异,利用这种差异经过反向传播去更新网络参数。
交叉熵原理?
在说交叉熵之前,先说一下信息量与熵。
信息量:它是用来衡量一个事件的不确定性的;一个事件发生的概率越大,不确定性越小,则它所携带的信息量就越小。假设X是一个离散型随机变量,其取值集合为X,概率分布函数为
我们定义事件
的信息量为:
熵:它是用来衡量一个系统的混乱程度的,代表一个系统中信息量的总和;信息量总和越大,表明这个系统不确定性就越大。
举个例子:假如小明和小王去打靶,那么打靶结果其实是一个0-1分布,X的取值有{0:打中,1:打不中}。在打靶之前我们知道小明和小王打中的先验概率为10%,99.9%。根据上面的信息量的介绍,我们可以分别得到小明和小王打靶打中的信息量。但是如果我们想进一步度量小明打靶结果的不确定度,这就需要用到熵的概念了。那么如何度量呢,那就要采用期望了。我们对所有可能事件所带来的信息量求期望,其结果就能衡量小明打靶的不确定度:
与之对应的,小王的熵(打靶的不确定度)为:
虽然小明打靶结果的不确定度较低,毕竟十次有9次都脱靶;但是小王打靶结果的不确定度更低,1000次射击只有1次脱靶,结果相当的确定。
交叉熵:它主要刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。假设概率分布p为期望输出,概率分布q为实际输出,下面公式为交叉熵,则
那么该公式如何表示,举个例子,假设N=3,期望输出为
,实际输出
和
那么:
通过上面可以看出,q2与p更为接近,它的交叉熵也更小。
但是需要注意的是:
Pytorch中的CrossEntropyLoss()函数
Pytorch中计算的交叉熵并不是采用,
这种方式计算得到的,而是交叉熵的另外一种方式计算得到的:
它是交叉熵的另外一种方式。
Pytorch中CrossEntropyLoss()函数的主要是将softmax-log-NLLLoss合并到一块得到的结果。
1、Softmax后的数值都在0~1之间,所以ln之后值域是负无穷到0。
2、然后将Softmax之后的结果取log,将乘法改成加法减少计算量,同时保障函数的单调性 。
3、NLLLoss的结果就是把上面的输出与Label对应的那个值拿出来(下面例子中就是:将log_output\logsoftmax_output中与y_target对应的值拿出来),去掉负号,再求均值。
官网有关CrossEntropy(交叉熵)的计算公式如下:
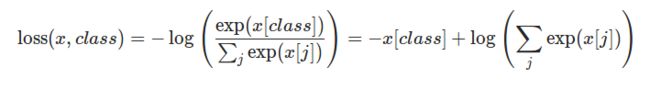
从公式我们就可以看出来,不过是取了某个logsoftmax之后的值并取负号而已。而取负号这个操作正是nn.nllloss函数的功用。所以说,CrossEntropy函数其实就相当于logsoftmax+nlllloss操作。
我们可以验证一下:
import torch
import torch.nn as nn
num=torch.Tensor([[1,2,3]])
a=torch.Tensor([1]).long()
ce=nn.CrossEntropyLoss()
ce=ce(num,a)
print(ce)
logS=nn.LogSoftmax()
logS=logS(num)
nll=nn.NLLLoss()
nll=nll(logS,a)
print(nll)
#输出
#tensor(1.4076)
#tensor(1.4076)
nn.MSELoss


这里显示的是平均数,其实是由函数参数决定的。不只是这个损失函数,其他损失函数也大多拥有这些函数参数,用于决定输出平均值还是一组数据中每个数据的损失值。
很多的loss函数都有size_average和reduce两个布尔类型的参数,因为一般损失函数都是直接计算batch的数据,因此返回的loss结果都是维度为(batch_size,)的向量。
1)如果reduce=False,那么size_average参数失效,直接返回向量形式的loss
2)如果redcue=true,那么loss返回的是标量。
2.a: if size_average=True, 返回loss.mean();#就是平均数
2.b: if size_average=False,返回loss.sum()
注意:默认情况下,reduce=true,size_average=true
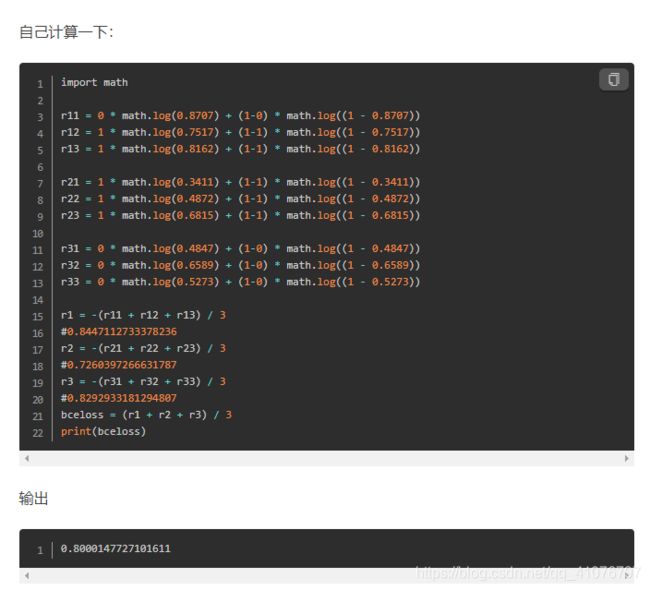
nn.BCELoss:
还有一类损失叫做BCELoss,写全了的话就是Binary Cross Entropy
Loss,就是交叉熵应用于二分类时候的特殊形式,一般都和sigmoid一起用,表达式就是二分类交叉熵:
数学公式为
其中t为目标值,o为预测值。
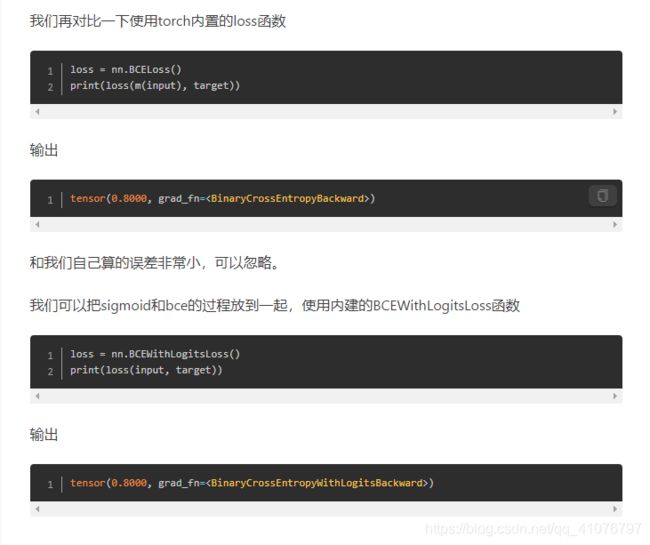
要记住,使用该损失函数之前一定要先进行sigmoid操作,CrossEntropyLoss与之不同的是内置了softmax操作,不需要人为提前进行该操作。
CrossEntropyLoss和BCELoss的激活函数是不同的,前者是softmax,后者是sigmoid。
关于sigmoid和softmax:


![[公式] 当 [公式] 时,熵将等于0,也就是说该事件的发生不会导致任何信息量的增加。](http://img.e-com-net.com/image/info8/768dec078892498ca92d671f4f09162f.jpg)
![[公式]](http://img.e-com-net.com/image/info8/951f5b6dba164b6195c1a2a7f1c6ab51.jpg)


![Loss = -w * [p * log(q) + (1-p) * log(1-q)]](http://img.e-com-net.com/image/info8/1c906f3052404a20a2ea3fcc31491803.png)