python kmean 多维_Python机器学习：Kmeans聚类

聚类算法直接从数据的内在性质中学习最优的划分结果或者确定离散标签类型。

虽然在 Scikit-Learn 或其他地方有许多聚类算法，但最简单、最容易理解的聚类算法可能还得算是 k-means 聚类算法了，在sklearn.cluster.KMeans中实现。首先还是先输入标准程序包：%matplotlib inline

import matplotlib.pyplot as plt

import seaborn as sns; sns.set()  # for plot styling

import numpy as np

01/ k-means简介

k-means 算法在不带标签的多维数据集中寻找确定数量的簇。最优的聚类结果需要符合以下两个假设。“簇中心点”(cluster center)是属于该簇的所有数据点坐标的算术平均值。

一个簇的每个点到该簇中心点的距离，比到其他簇中心点的距离短。

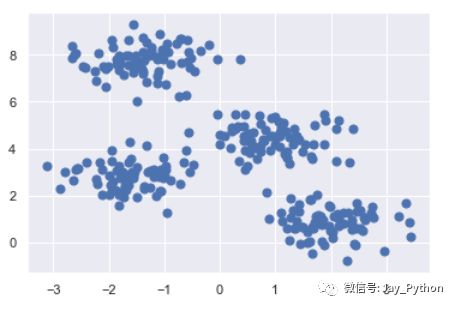
这两个假设是 k-means 模型的基础，后面会具体介绍如何用该算法解决问题。先通过一个简单的数据集，看看 k-means 算法的处理结果。首先，生成一个二维数据集，该数据集包含 4 个明显的簇。由于要演示无监督算法，因此去除可视化图中的标签:

from sklearn.datasets.samples_generator import make_blobs

X, y_true = make_blobs(n_samples=300, centers=4,

cluster_std=0.60, random_state=0)

plt.scatter(X[:, 0], X[:, 1], s=50);

通过肉眼观察，可以很轻松地挑选出 4 个簇。而 k-means 算法可以自

动完成 4 个簇的识别工作，并且在 Scikit-Learn 中使用通用的评估器API：from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters=4)

kmeans.fit(X)

y_kmeans = kmeans.predict(X)

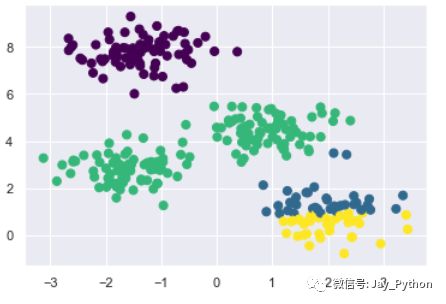
下面用带彩色标签的数据来展示聚类结果。同时，画出簇中心点，这些簇中心点是由 k-means 评估器确定的：plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')

centers = kmeans.cluster_centers_

plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.5);

告诉你个好消息，k-means 算法可以(至少在这个简单的例子中)将点指定到某一个类，就类似于通过肉眼观察然后将点指定到某个类。但你可能会好奇，这些算法究竟是如何快速找到这些簇的，毕竟可能存在的簇分配组合方案会随着数据点的增长而呈现指数级增长趋势，如果要做这样的穷举搜索需要消耗大量时间。好在有算法可以避免这种穷举搜索——k-means 方法使用了一种容易理解、便于重复的期望最大化算法取代了穷举搜索。

02/ k-means算法：期望最大化

期望最大化(expectation-maximization，E-M)是一种非常强大算法，应用于数据科学的很多场景中。k-means 是该算法的一个非常简单并且易于理解的应用，下面将简单介绍 E-M 算法。简单来说，期望最大化方法包含以下步骤。

(1) 猜测一些簇中心点。

(2) 重复直至收敛。

a. 期望步骤(E-step)：将点分配至离其最近的簇中心点。

b. 最大化步骤(M-step)：将簇中心点设置为所有点坐标的平均

值。

期望步骤(E-step 或 Expectation step)不断更新每个点是属于哪一个簇的期望值，最大化步骤(M-step 或 Maximization step)计算关于簇中心点的拟合函数值最大化对应坐标(argmax 函数)——在本例中，通过简单地求每个簇中所有数据点坐标的平均值得到了簇中心点坐标。

关于这个算法的资料非常多，但是这些资料都可以总结为：在典型环境下，每一次重复 E-step 和 M-step 都将会得到更好的聚类效果。

将这个算法在下图中可视化：

如图所示，数据从初始化状态开始，经过三次迭代后收敛。下图显示的是聚类的交互式可视化版本，详情请参见 GitHub 在线附录(https://github.com/jakevdp/PythonDataScienceHandbook)中的代码。

k-means 算法非常简单，只要用几行代码就可以实现它。以下是一个非常基础的 k-means 算法实现:from sklearn.metrics import pairwise_distances_argmin

def find_clusters(X, n_clusters, rseed=2):

# 1.随机选择簇中心点

rng = np.random.RandomState(rseed)

i = rng.permutation(X.shape[0])[:n_clusters]

centers = X[i]

while True:

# 2a.基于最近的中心指定标签

labels = pairwise_distances_argmin(X, centers)

# 2b.根据点的平均值找到新的中心

new_centers = np.array([X[labels == i].mean(0)

for i in range(n_clusters)])

# 2c.确认收敛

if np.all(centers == new_centers):

break

centers = new_centers

return centers, labels

centers, labels = find_clusters(X, 4)

plt.scatter(X[:, 0], X[:, 1], c=labels,

s=50, cmap='viridis');

虽然大部分可用的聚类算法底层其实都是对上述示例的进一步扩展，但上述函数解释了期望最大化方法的核心内容。

使用期望最大化算法时的注意事项

在使用期望最大化算法时，需要注意几个问题。

可能不会达到全局最优结果

首先，虽然 E–M 算法可以在每一步中改进结果，但是它并不保证可以获得全局最优的解决方案。例如，如果在上述简单的步骤中使用一个随机种子(random seed)，那么某些初始值可能会导致很糟糕的聚类结果。

centers, labels = find_clusters(X, 4, rseed=0)

plt.scatter(X[:, 0], X[:, 1], c=labels,

s=50, cmap='viridis');

虽然 E–M 算法最终收敛了，但是并没有收敛至全局最优配置。因此，该算法通常会用不同的初始值尝试很多遍，在 Scikit-Learn 中通过n_init 参数(默认值是 10)设置执行次数。

簇数量必须事先定好。

k-means 还有一个显著的问题：你必须告诉该算法簇数量，因为它

无法从数据中自动学习到簇的数量。如果我们告诉算法识别出 6 个簇，

它将很快乐地执行，并找出最佳的 6 个簇：

结果是否有意义是一个很难给出明确回答的问题。有一个非常直观的方法，但这里不会进一步讨论，该方法叫作轮廓分析(http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_silhouette_analysis.html)。

不过，你也可以使用一些复杂的聚类算法，有些算法对每个簇的聚类效果有更好的度量方式(例如高斯混合模型，Gaussian mixturemodels)，还有一些算法可以选择一个合适的簇数量(例如DBSCAN、均值漂移、近邻传播，这些都是sklearn.cluster的子模块)。

k-means 算法只能确定线性聚类边界。

k-means 的基本模型假设(与其他簇的点相比，数据点更接近自己

的簇中心点)表明，当簇中心点呈现非线性的复杂形状时，该算法通常

不起作用。

k-means 聚类的边界总是线性的，这就意味着当边界很复杂时，算

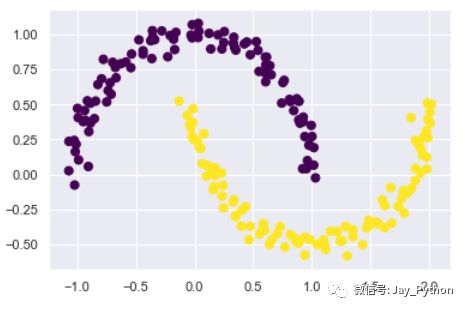
法会失效。用下面的数据来演示 k-means 算法得到的簇标签

from sklearn.datasets import make_moons

X, y = make_moons(200, noise=.05, random_state=0)

labels = KMeans(2, random_state=0).fit_predict(X)

plt.scatter(X[:, 0], X[:, 1], c=labels,

s=50, cmap='viridis');

这个情形让人之前介绍的内容，当时我们通过一个核变换将数据投影到更高维的空间，投影后的数据使线性分离成为可能。或许可以使用同样的技巧解决 k-means 算法无法处理非线性边界的问题。

这种核 k-means 算法在 Scikit-Learn 的SpectralClustering评估器中实现，它使用最近邻图(the graph of nearest neighbors)来计算数据的高维表示，然后用 k-means 算法分配标签：

from sklearn.cluster import SpectralClustering

model = SpectralClustering(n_clusters=2, affinity='nearest_neighbors',

assign_labels='kmeans')

labels = model.fit_predict(X)

plt.scatter(X[:, 0], X[:, 1], c=labels,

s=50, cmap='viridis');

可以看到，通过核变换方法，核 k-means 就能够找到簇之间复杂的非线性边界了。

当数据量较大时，k-means 会很慢

由于 k-means 的每次迭代都必须获取数据集所有的点，因此随着数

据量的增加，算法会变得缓慢。你可能会想到将“每次迭代都必须使用所有数据点”这个条件放宽，例如每一步仅使用数据集的一个子集来更新簇中心点。这恰恰就是批处理(batch-based) k-means 算法的核心思

想，该算法在 sklearn.cluster.MiniBatchKMeans 中实现。该算法的接口和标准的 KMeans 接口相同，后面将用一个示例来演示它的用

法。