Python实现K-means聚类分析
k均值聚类算法(k-means clustering algorithm)是一种迭代求解的聚类分析算法,其步骤是,预将数据分为K组,则随机选取K个对象作为初始的聚类中心,然后计算每个对象与各个种子聚类中心之间的距离,把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本,聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有(或最小数目)对象被重新分配给不同的聚类,没有(或最小数目)聚类中心再发生变化,误差平方和局部最小。其基本思想是:基于使聚类性能指标最小化,所用的聚类准则函数是聚类集中每一个样本点到该类中心的距离平方之和,并使其最小化。
步骤
①假设分为k类,选则样本中前k个值作为k类的初始聚类中心;
②将模式样本集的每一样本按最小距离原则分配给k个聚类中心,聚为k类;
③根据第二步聚类结果计算新的聚类中心,计算方法为类内各样本点值之和除以类 内样本点的个数;
④判断本次聚类中心与上次聚类中心是否一样,若一样,则聚类结束;若不一样,则重复二三四步骤。
代码
加入需要用到的python第三方库:
import numpy as np
import matplotlib.pyplot as plt构建一个函数calcu()实现根据聚类中心算每个样本点到聚类中心的最小距离,根据最小距离重新分为k类,利用matplotlib.pyplot可视化聚类结果;
def calcu(x, k):
global center, classk, count # 初始化
classk = []
sum = []
for j in range(k):
classk.append([])
sum.append([0, 0])
for i in range(len(x)): # 计算每一个样本点到所有聚类中心的距离,
distance = []
for j in range(k):
dis = (x[i][0]-center[j][0])**2 + (x[i][1]-center[j][1])**2
distance.append(dis)
min1 = min(distance) # 求出最小距离
# print("第{}个样本点的最短距离为:".format(i+1), min1)
adress = distance.index(min1)
classk[adress].append(x[i]) # 将第i个样本点加入到对应聚类中心最近的类中
# print(classk)
N = []
# Z = []
for j in range(k): # 计算新的聚类中心
n1 = len(classk[j])
N.append(n1)
for i in range(N[j]):
sum[j] += classk[j][i]
z1 = sum[j]/N[j]
center.append(z1)
# print(Z[j])
# center.append(Z[j])
print("分类结果为:", classk)
# 画图
# print("count为:", count)
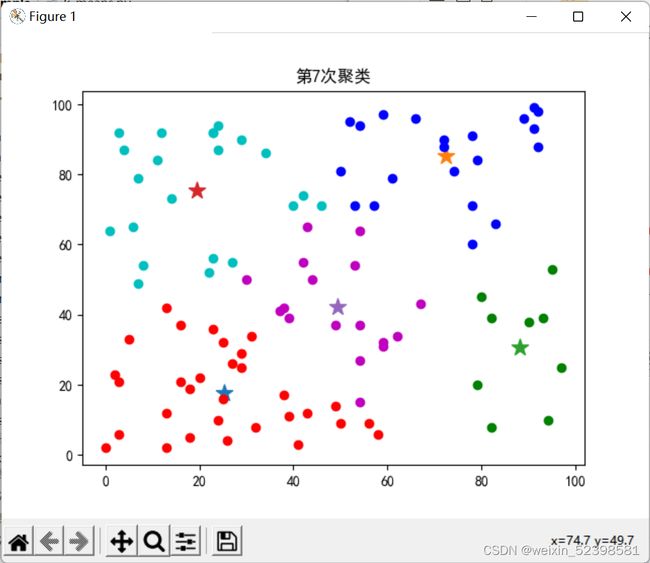
plt.title("第" + str(count) + "次聚类")
for i in range(k, k*2):
plt.scatter(center[i][0], center[i][1], marker='*', s=150)
for i in range(k):
for point in range(N[i]):
plt.scatter(classk[i][point][0], classk[i][point][1], c=('r' if i == 0 else 'b' if i == 1 else 'g'
if i == 2 else 'c' if i == 3 else 'm' if i == 4 else 'y'))
plt.show()
count +=1
构建一个函数panduan()实现聚类是否终止的判断;
def panduan(k):
abcde = 0
for i in range(k):
if center[i][0] == center[i+k][0] and center[i][1] == center[i+k][1]:
abcde += 1
return abcde构建一个函数circu()实现聚类结果的迭代,设置最大迭代次数,调用calcu(),panduan()完成K-means聚类分析;
def circu(x, k): # x为样本
global center, classk, count
count = 1
center = []
for i in range(k):
center.append(x[i])
calcu(x, k)
for i in range(30): # 判断分类是否完成,设置最大迭代次数
if panduan(k) == k:
print("分类完成!")
break
else:
del center[0:k]
print("聚类中心为:", center)
calcu(x, k)在主函数中生成随机样本点,并规定样本点的范围与维数,输入聚类数后运行查看结果。这里设置100个二维样本点,分为5类。
if __name__ == '__main__':
x = np.random.randint(0, 100, size=[100, 2])
circu(x, 5)运行后将会把每一次聚类的结果可视化,当聚类完成后,提示聚类完成。
总结
贝叶斯估计应用于多个领域如人工智能、专家系统等,K-means聚类分析是无监督学习领域最为经典的算法之一。通过此次实践将一些难以理解的知识实例化,使其更加通俗易懂,对贝叶斯估计和K-means聚类分析在实际应用中有了一个具体的认知,使知识更加具体系统化,对以后的学习打下了良好的基础。