机器学习——KNN算法

机器学习——KNN算法

---

---

前言

机器学习笔记

---

一、KNN原理基础

KNN的算法原理，可以简单如下描述：
一个数据集中存在多个已有标签的样本值，这些样本值共有的n个特征构成了一个多维空间N。当有一个需要预测/分类的样本x出现，我们把这个x放到多维空间n中，找到离其距离最近的k个样本，并将这些样本称为最近邻（nearest neighbour）。对这k个最近邻，查看他们的标签都属于何种类别，根据”少数服从多数，一点算一票”的原则进行判断，数量最多标签类别就是x的标签类别。其中涉及到的原理是“越相近越相似”，这也是KNN的基本假设。 KNN中的K代表的是距离需要分类的测试点x最近的K个样本点，如果不输入这个值，KNN算法中的重要部分“选出K个最近邻”就无法实现。

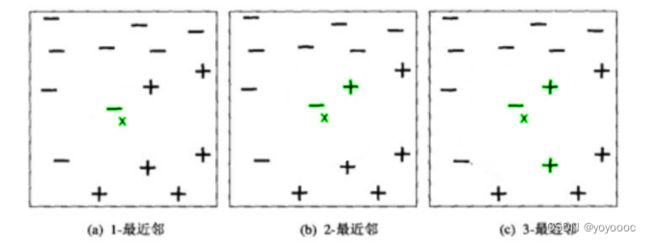
若数据集只有两个特征，则针对于数据集的描述可用二维平面空间图来表示。如下图，二位平面空间的横坐标是特征1，纵坐标是特征2，每个样本点的分类（正或负）是该组样本的标签。图中给出了位于平面中心的，需要分类的数据点x，并用绿色分别标注了k为1，2，3时的最近邻状况。在图a中，x的1-最近邻是一个负例，因此x被指派到负类。图c中，3-最近邻中包括两个正例和一个负例，根据“少数服从多数原则”，点x被指派到正类。在最近邻中正例和负例个数相同的情况下（图b），算法将随机选择一个类标号来分类该点。

二、sklearn的基本建模流程

#======注意该代码仅作展示，无法运行=======#

from sklearn.neighbors import KNeighborsClassifier #导入需要的模块

clf = KNeighborsClassifier(n_neighbors=k)          #实例化
clf = clf.fit(X_train,y_train)                     #用训练集数据训练模型
result = clf.score(X_test,y_test)                  #导入测试集，从接口中调用需要的信息

三、KNN算法调优：选取最优的K值

从KNN的原理中可见，是否能够确认合适的k值对算法有极大的影响。如果K太小，则最近邻分类器容易受到由于训练数据中的噪声而产生的过分拟合的影响；相反。如果k太大，最近邻分类器可能会将测试样例分类错误，因为k个最近邻中可能包含了距离较远的，并非同类的数据点（如下图，k近邻由绿色表示）。因此，超参数K的选定是KNN中的头号问题。

那我们怎样选择一个最佳的K呢？在这里我们要使用机器学习中的神器：参数学习曲线。参数学习曲线是一条以不同的参数取值为横坐标，不同参数取值下的模型结果为纵坐标的曲线，我们往往选择模型表现最佳点的参数取值作为这个参数的取值。

以手写数据集为例：

代码如下（示例）：

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
#探索数据集
data = load_digits()

Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y              #特征和标签
                                           ,test_size=0.3    #测试集所占的比例
                                           ,random_state=1)
# 绘制学习曲线
score = [] #用来存放模型预测结果
krange = range(1,20) 

for i in krange:
   clf = KNeighborsClassifier(n_neighbors=i)
   clf = clf.fit(Xtrain,Ytrain)
   score.append(clf.score(Xtest,Ytest))
score
bestK = krange[score.index(max(score))]
print(bestK)
print(max(score))

plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei'']

plt.figure(figsize=(6,4),dpi=80)  #dpi是像素值
plt.plot(krange,score)

plt.title('K值学习曲线',fontsize=15)
plt.xlabel('K值',fontsize=12)
plt.ylabel('预测准确率',fontsize=12)
plt.xticks(krange[::3])  # x轴刻度
plt.show()

四、KNN中距离的相关讨论

1. KNN使用的是什么距离？

KNN属于距离类模型，原因在于它的样本之间的远近是靠数据距离来衡量的。欧几里得距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离等都是很常见的距离衡量方法。KNN中默认使用的是欧氏距离（也就是欧几里得距离）。

2. 距离类模型的归一化需求

我们再看一下，欧氏距离的计算公式： $d(A,B)=\sqrt{{\sum }_{i=1}^n(x_{iA}-x_{iB}{)}^2}$

试想看看，如果某个特征 的取值非常大，其他特征的取值和它比起来都不算什么，那距离的大小很大程度上都会由这个巨大特征 来决定，其他的特征之间的距离可能就无法对 (,) 的大小产生什么影响了，这种现象会让KNN这样的距离类模型的效果大打折扣。
有的特征数值很大，有的特征数值很小，这种现象在机器学习中被称为“量纲不统一”.

在实际分析情景当中，绝大多数数据集都会存在各特征值量纲不同的情况，此时若要使用KNN分类器，则需要先对数据集进行归一化处理，即是将所有的数据压缩到同一个范围内。这样可以避免模型偏向于数值很大但本身可能不是那么重要的一些特征。

思考：先切分训练集和测试集，还是先进行归一化？
**真正正确的方式是，先分训练集和测试集，再归一化！**为什么呢？想想看归一化的处理手段，我们是使用数据中的最小值和极差在对数据进行压缩处理，如果我们在全数据集上进行归一化，那最小值和极差的选取是会参考测试集中的数据的状况的。因此，当我们归一化之后，无论我们如何分割数据，都会由一部分测试集的信息被“泄露”给了训练集（当然，也有部分训练集的信息被泄露给了测试集，但我们不关心这个），这会使得我们的模型效果被高估。

#导入所需各种模块和包
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler as mms
from sklearn.datasets import load_wine

#导入数据集并提取特征和标签
data = load_wine()
X = data.data
y = data.target

#切分训练集和测试集
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size=0.3,random_state=0)
#数据归一化
MMS = mms().fit(Xtrain)              #这一步是在学习训练集，生成训练集上的极小值和极差
Xtrain_mms = MMS.transform(Xtrain)   #用训练集上的极小值和极差归一化训练集
Xtest_mms = MMS.transform(Xtest)     #用训练集上的极小值和极差归一化测试集
#建模并评估结果
clf = KNeighborsClassifier()  
clf = clf.fit(Xtrain_mms,Ytrain)              
score = clf.score(Xtest_mms,Ytest)           
score
#预测新样本，并查看样本的预测结果
y_pred = clf.predict(Xtest_mms)
y_pred
(y_pred == Ytest).sum() #查看预测正确的样本个数
(y_pred == Ytest).sum()/Ytest.shape[0]  #预测准确率也可以这样算

---

五、 KNN算法的优缺点

1. 应用广泛
   此外，最近邻分类属于一类更广泛的技术，这种技术称为基于实例的学习，它使用具体的训练实例进行预测，而不必去维护基于数据建立起来的模型。
2. 对样本分类边界不规则的情况较为友好
   经过长期的实践发现，KNN算法适用于样本分类边界不规则的情况。由于KNN主要依靠周围有限的邻近样本，而不是靠判别类域的方法来确定所属类别，因此对于类域的交叉或重叠较多的待分样本集来说，KNN算法比其他方法要更有效。
3. 计算效率低，耗费计算资源较大
   KNN必须对每一个测试点来计算到每一个训练数据点的距离，并且这些距离点涉及到所有的特征，当数据的维度很大，数据量也很大的时候，KNN的计算会成为诅咒，大概几万数据就足够让KNN跑几个小时了。计算效率低，耗费计算资源较大是KNN最致命的缺点。
4. 抗噪性较弱，对噪声数据（异常值）较为敏感
   最近邻分类器基于局部信息进行预测，正是因为这样的局部分类决策，最近邻分类器（k很小时）对噪声非常敏感。
5. 模型不稳定，可重复性较弱
   最近邻分类器可以生成任意形状的决策边界，这样的决策边界有很高的可变性，因为它们依赖于训练样例的组合。增加最近邻的数目可以降低这种可变性。