通用协议（七）两方安全计算-恶意模型

在两方安全计算中的恶意敌手模型

一些基础的问题

1.第一点，（恶意终止-公平性问题）没有任何方法能强制一方参与到协议中，也就是说一种恶意的行为包括阻止这个协议正常开始执行，或者更一般的行为是在任何时刻终止参与，导致协议中断。特别是，一个参与方获得了期望的结果后，终止协议。我们强调在通信模型的设计中，我们不能将一方发送消息的前提条件设置成为另一方发送一个正确的消息，因为在通信中，无法保证所有的消息都是有顺序的，这也暗示了可能存在的恶意行为。因此没有任何的两方协议能够防御一方获得期望输出后终止协议这种行为。换句话说，这个协议能够展示出完美的“公平性”，即双方共同获得结果，这无法在两方计算中实现，（往往在协议的设计时，我们会提及这个概念），所有我们放弃去证明这种公平的存在，但是可以相对的实现部分的公平属性。

2.第二点，（恶意输入问题）很明显对于恶意的敌手来说，其输入可能并不合法，没有任何方法对于协议来说能够看出哪个收到的输出来自于声明发送的一方。或者说，去保护恶意行为从修改他的输入。

综上所述，在协议的执行中有三种问题我们是无法避免的：
第一种：参与方拒绝参与协议。
第二种：参与方替换了自己应该的输入。
第三种：参与方提前终止协议。

因此，如果一个两方协议是安全的，如果敌手的行为本质上是由以上的三种三种方式限制的。这意味着，我们应该定义一个理想模型中相应的应为，并且定义安全性，然后安全协议的执行在真实模型下可以被理想函数所模拟。（这里其实就说明了，思维惯性我们应该会倾向于用现实模型靠向理想模型，但是实际上用理想模型靠向现实模型这是更加合理的，更加的严格）

实际的定义

The Ideal Model 理想模式

根据上文的讨论，我们将允许在理想模型中任何都不能阻止的在现实中的事情。另一种看待这个问题的方式为，我们假设存在一个可信第三方，但是任何的一方都无法保护确定的恶意行为。特别的，我们允许一个恶意的敌手在理想模型中拒绝参与或者替换他的本地输入。显然，这两件事都不能被可信第三方阻止。因此我们假设第一方有在可信第三方发送数据给第二参与方之前终止协议的能力。这个能力第二方并不能持有。因此在理想的模型下一个执行结果是这样的：

input : 每一方获得的一个输入，定义为u；

Sending inputs to the trusted party: 一个诚实方总是发送 u 给与可信方，一个恶意敌手可能会依据u 或者其他的掷硬币序列，辅助输入给与输入或者终止协议；

The trusted party answers the first party： 可信方在此处，可以获得一个输入的对（x,y) ; 然后TPP会首先回复第一方内容，否则（TPP仅仅只接受到了一个输入方内容）TPP直接回复一个终止符号。

The trusted party answers the second party：在这种情况下，第一方如果是恶意的，那么他会依据第一方自己的输入和可信方的输出决定是终结这个协议还是不终结这个协议。在这种情况下，即第一方是恶意的情况下，TPP发送终结符号给第二方，否则，TPP发送第二方应得的输出给与第二方。

Outputs：对于输出的情来看，一个诚实方终究会输出它从TPP处获得的消息。一个恶意的参与方会根据自己获得内容和初始化的内容输出一个随机的可在多项式时间计算函数的值。

事实上，不是一般性，我们假设所有的参与方都将输出发送给了TPP，而不是假定他们中断了协议。这样的假设是可以实现的通过使得TPP使用一些默认的值以防参与方没有参与到协议中来。因此理想模型被如下定义，算法B1 和B2 表现了所有可能的操作在模型中。B1和B2定义如下：


其中 x, y 为B1和B2的输入，z 是辅助输入，r 是产生辅助输入的一个随机的带。如果第一方和第二方是诚实的那么B1输出的就是x. B2 输出的就是y. 同样的，如果第一方是恶意的参与方，他决定终止这个协议，那么他在获得期望的输出后做如下的操作：

v 是从TPP接收到输出，并且整个算法B1输出中终止符号。在这种情况下，第一方的本地输出如下：

如果第一方没有输出终止符号，那么第一方本地输出和上文是相同的，仅仅是缺少一个终止符号而已。相似的第二方的本地输出为B2（y,z,r,v）这其实如果两方都是诚实的那么所有人的输出都是v.

Malicious adversaries in the ideal model

定义太长，此处直接拷贝书上的内容：

此处的定义和之前的定义类似，不同的是，这里假定了参与方的初始化输出不变。接下来依然是几个纯定义公式：

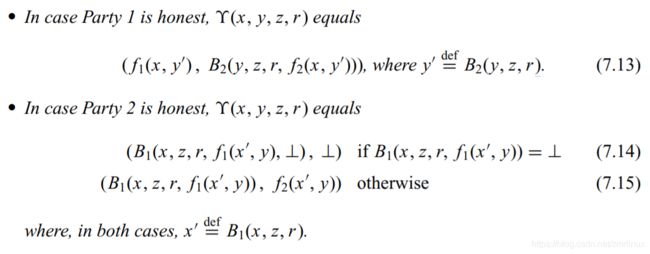
如图中定义，如果第一方是诚实的，那么整个理想模型的视图如下（其实这里文中并没有称之为视图，但是其实本质上就是整个理想模型的视图），例如在公式7.13 中，如果第一方是诚实的，那么第一方按照正常函数执行输出，第二方按照B2算法执行，输出为第二方的输出结果。类似的，如果第二方是诚实的，第一方是不诚实的，那么理想协议如7.14 所示，因为第一方不诚实，所以会在第一方获得期望的输出后，直接中断协议，所以第二方的无法获得内容，协议因此中断，所以输出终止符号。第一方由算法B1给出输出视图。此处，其实B1是可能使用替换书输入来调用诚实参与方的。如果第一方为恶意敌手却没有中断这个协议的执行，那么我们可以看出来式子7.15 其实就是这种描述。在这些所有的情况下，TPP计算 f(B1(x,z,r), y) 并且P1输出一个字符串取决于，第一方的给与TPP的输入和整个x, z , r. 同样的，等式7.13表现出了第二方恶意行为。

Execution in the Real Model

进一步，我们考虑现实模型，在现实模型中，没有可信第三方的帮助。在这种情况下，恶意的一方会采取任何可行的策略。也就是说，是可以由概率多项式时间算法实现的任意操作，例如获取辅助输入。特别是，敌手参与方可以中断协议在任何的地方，此时另一方却没有任何的输出。与理想协议中类似，我们将采用算法来描述各方的策略。
定义如下所示：

和之前使用的策略类似，在现实模型下，敌手的行为以及环境定义如上图，还是很容易理解的。在真实模型下存在两个参与方，分别使用概率多项式算法A1 和A2 ，A1接受输入x 和辅助输入z , A2 接受输入y 和辅助输入z.

Security as Emulation of Real Execution in the Ideal Model

安全性作为真实执行过程的模拟在理想模型中
当我们定义了理想和现实模型之后，我们就获得了对应的安全定义。不是一般性，这个定义断言一个安全的两方安全计算协议模拟一个理想模型。这是通过模拟来论证的，允许的敌手在理想模型下是能够模拟的一个安全真实协议的执行过程的在任何的可能敌手下。就是说，在理想模型中可以模拟安全真实协议的执行。其实和之前说的一样，理想的模型能够模拟出现实的执行过程，那么一定证明现实的执行过程是安全的。

Security in the malicious model 安全在恶意敌手当中

在恶意敌手模型中的安全如下：

一个重要的属性是上述定义在恶意敌手下实现了保密计算。这就是说，所有的敌手能够学习通过参与这个协议使用任何可能的协议，能够本质的推断出来仅仅从相应的输出。也就是说各方仅仅只能从参与获得的内容去学习推断输出。另一种属性通过上文定义的是正确性，这意味着诚实方的输出必须和诚实方输入的内容相对应。更进一步，敌手对应的元素必须选择不能影响诚实方的输入。我们定义这两种属性是非常容易实现的使用上述定义，但是这个定义并不能被实现通过这两个属性。

以上内容参考《Foundations.of.Cryptography.Volume.2.Basic.Applications(Oded.Goldreich)》