CNN的Python实现——第二章:线性分类器
文章目录
- 第二章:线行分类器
-
- 2.1 线性模型
-
- 2.1.1 线性分类器
- 2.1.2 理解线性分类器
- 2.1.3 代码实现
- 2.2 softmax损失函数
-
- 2.2.1 损失函数的定义
- 2.2.2 概率解释
- 2.2.3 代码实现
- 2.3 优化
- 2.4 梯度下降法
-
- 2.4.1 梯度的解析意义
- 2.4.2 梯度的几何意义
- 2.4.3 梯度的物理意义
- 2.4.4 梯度下降法代码实现
- 2.5 牛顿法
- 2.6 机器学习模型统一结构
- 2.7 正则化
-
- 2.7.1 范数正则化
- 2.7.2 提前终止训练
- 2.7.3 概率的进一步解释
第二章:线行分类器
2.1 线性模型
2.1.1 线性分类器
属性 x i x_i xi 和 参数 w w w 的线性函数为:
![]()
其中,输出 s s s 是分值, D D D 个 w i w_i wi 组成参数 w w w ,也称权重向量, b b b 是偏置参数。由于 s s s 是标量,只能表示某个类别的分值,不能表示所有类别的分值。为了得到 K K K 个分值,则需 K K K 个线性函数:
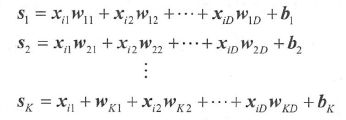
第 i i i 个方程表示第 i i i 类的分值函数,也称为第 i i i 个分类器。为了简化书写,可以写成矩阵形式:
![]()
注意此时 s s s 是分值行向量, b b b 是偏置行向量, W W W 是权重矩阵,每列由 w i w_i wi个列向量构成。
在MNIST 中,各向量或矩阵的维度为:
- s s s 是 [ 1 × K ] = [ 1 × 10 ] [ 1 \times K] = [1 \times 10] [1×K]=[1×10],
- b b b 是 [ 1 × K ] = [ 1 × 10 ] [ 1 \times K] = [1 \times 10] [1×K]=[1×10],
- x i x_i xi 是 [ 1 × D ] = [ 1 × 784 ] [ 1 \times D] = [1 \times 784] [1×D]=[1×784] ,
- W W W 是 [ D × K ] = [ 784 × 10 ] [ D \times K] = [784 \times 10] [D×K]=[784×10]。
对于线性模型,需要强调如下几点。
- 第一,进行多分类,只需一个矩阵乘法 x i W x_iW xiW 和矩阵加法,每个分类器就是 W W W 的一个列向量。
- 第二,训练集 ( x i , y i ) (x_i,y_i) (xi,yi) 是 给定且不可改变的,可变的是权重 W W W 和偏置向量 b b b。机器学习的日的就是通过优化算法得到这些参数的最优值,使得模型计算出来的分值向量和训练集中样本的真实类别标签相符。何谓相符,详见2 .2 节。
- 第三,模型训练的结果是得到最优参数 W W W 和 b b b 。一旦训练完成,就不再需要训练集。因为预测样本类别时,只需计算分值向量,不需要训练集。
2.1.2 理解线性分类器
线性分类器看作模板匹配: w i w_i wi 对应一个类别模板,分类就是找到 x i x_i xi 和哪个模板最相似。从这个角度来看,线性分类器就是利用学习得到的模板,做模板匹配,使用负内积来计算图像与模板的距离,距离越小,说明越相似。
线性分类器只能对线性可分的样本进行有效分类,线性可分指可以用一个线性函数把多类样本分开。线性不可分指有部分样本用线性分类器划分时会产生分类错误。
对于线性不可分样本集,可以采用神经网络来分类,神经网络就是线性分类器的升级版本。
2.1.3 代码实现
线性函数为: S = X W + B S=XW+B S=XW+B
每个样本的分值向量组成分值矩阵 S S S 的一行,每个样本属性向量组成样本属性矩阵 X X X 的一行。矩阵 X X X 也称为数据矩阵,偏置矩阵 B B B 的每行都是偏置向量 b b b 。代码如下:
import numpy as np
D = 784 # 数据维度
K = 10 # 类别数
N = 128 # 样本数量
X = np.random.randn(N, D) # 数据矩阵,每行一个样本
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))
scores = np.dot(X, W) + b # 广播机制
这里有一个小trick, b b b 是行向量, X W XW XW 得到的结果是 矩阵,严格来说,最后一句是错误的。但是 Numpy 里面有一个广播内部机制,自动完成矩阵扩展工作。
2.2 softmax损失函数
2.2.1 损失函数的定义
损失函数( loss function ,也叫代价函数, cost function )用来评价分值向量的好坏。分值向量与真实标签之间的差异越大,损失函数值就越大,反之则越小。
设分值向量 s = ( s 1 , s 2 , . . . , s k ) s = (s_1,s_2,...,s_k) s=(s1,s2,...,sk) ,因为分值可正可负,如果直接采用所占比例,对于负的分值,不能反映其相对大小。因此,运用数学技巧,把分值映射为正值,且单调递增。指数函数刚好满足此性质: e x p s = e s exps=e^s exps=es
定义归一化向量 n o r m s = ( e s 1 , e s 2 , . . . , e s K ) / ∑ i = 1 K e s i norms = ({e^{{s_1}}},{e^{{s_2}}},...,{e^{{s_K}}})/\sum\limits_{i = 1}^K {{e^{{s_i}}}} norms=(es1,es2,...,esK)/i=1∑Kesi,这样每个元素取开区间 ( 0 , 1 ) (0,1) (0,1) 的值,且所有元素之和为1.
真实类别的分值应当取最高分值,且越高越好,这意味着希望真实类别的归一化向量的元素 n s y ns_y nsy 的取值接近1 。如果取值小于1 ,需对其进行惩罚。
一个直观的损失函数为 1 − n s y 1-ns_y 1−nsy ,当取 n s y ns_y nsy 为1 时,损失为 0 ;当 n s y ns_y nsy 取0 时,损失为 1, 即最大损失,满足要求。但该损失函数的惩罚力度太小,不利于后面的参数优化。
我们希望当 1 − n s y 1-ns_y 1−nsy 取0 时,损失值很大,趋近无穷大;当 1 − n s y 1-ns_y 1−nsy 取 1 时,损失值为0 。不难想到,负对数函数刚好满足这个条件, 故损失函数采用 − l o g ( n s y ) -log(ns_y) −log(nsy) ,我们需要最小化损失函数。
把上述公式综合在一起,得到softmax 损失函数的定义: L i = − l o g ( e s y i / ∑ j = 1 K e s j ) L_i=-log(e^{s_{y_i}}/\sum\limits_{j = 1}^K {{e^{{s_j}}}}) Li=−log(esyi/j=1∑Kesj)
其中 y i y_i yi 是样本 i i i 的标签,即样本真实类别在类别集合中的序号。
举个例子:

上面计算了一个样本的损失值,如果计算多个样本的损失值,则最终损失值取平均值。
2.2.2 概率解释
归一化向量norms 的每个元素均大于0 小于 1,且和为 1,所以可以将其看作归属各个类别的概率。损失函数可以看作真实类别的负对数概率,希望其最小。这个也可以通过极大似然来解释,负对数概率最小,等价概率最大,即希望真实类别样本出现的概率最大,最容易被采样到。由于真实类别的慨率不可能等于1 ,所以总会存在损失。只要有损失,学习就不会停止:真实类别的分值总会增加,错误类别的分值总会降低,损失值总是能够更小,这样会导致永远地学习,最终引起过拟合。缓解这种过拟合的方法是: 当真实类别的概率值大于阈值(如0.99 ),则认为损失为0 ,停止学习。
2.2.3 代码实现
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import numpy as np
D = 784
K = 10
N = 128
# scores是分值矩阵,每行代表一个样本
scores = np.random.randn(N, K)
# 样本标签
y = np.random.randint(K, size = N)
# 指数化分值矩阵
exp_scores = np.exp(scores)
# 样本归一化系数
exp_scores_sum = np.sum(exp_scores, axis=1)
# 样本真实类别的归一化分值
corect_probs = exp_scores[range(N), y]/exp_scores_sum
# 负对数损失函数
corect_logprobs = -np.log(corect_probs)
# 平均损失
data_loss = np.sum(corect_logprobs)/N
2.3 优化
基于模型(如线性模型)得到分值向量,根据损失函数评价参数的好坏,如何寻找最优的参数,使损失最小?这就是最优化。
对于简单的优化问题,可以使用解析法,即直接求解出最优参数的解析解。
但对于复杂的优化问题,很难得到解析解,此时一般采用数值迭代法,即首先随机初始化解 x 0 x_0 x0,然后利用迭代公式 x k = ϕ ( x k − 1 ) x_k = \phi (x_{k-1}) xk=ϕ(xk−1),且保证 f ( x k ) < f ( x k − 1 f(x_k ) < f(x_{k-1} f(xk)<f(xk−1 )计算数列 x k x_k xk,如果 x k x_k xk 收敛到 x ∗ x^* x∗,则 x ∗ x^* x∗ 就是(局部)最优解并且 x ∗ x^* x∗ 是最小值。
迭代法需要考虑收敛速度的问题,即需要多少次迭代才能达到指定的精度要求(近似收敛到 x ∗ x^* x∗ )。需要的迭代次数越少,算法收敛速度就越快,这是我们所希望的。
理论上说,有3 种收敛速度一一次线性、线性和二次收敛,这3种收敛速度依次加快。对于非凸优化问题,最好的情况下也只能达到次线性收敛速度,收敛速度十分慢。
梯度下降法是最优化的经典迭代法,牛顿迭代法是解方程的经典迭代法,下面将分别介绍这两种方法。
2.4 梯度下降法
梯度下降法是最优化的经典理论,有严格的数学理论支撑。
2.4.1 梯度的解析意义
2.4.2 梯度的几何意义
2.4.3 梯度的物理意义
2.4.4 梯度下降法代码实现
alpha = 1
epslon = 0.5
iter_num = 100
xO = 1
def f(x):
return alpha*x**2/2
def df (x):
return alpha*x
def GD_update (x):
return x - epslon*df(x)
x = xO
for k in range(iter_num):
x = GD_update(x)
print(k, x, f(x), df(x))
读者可以尝试不同的学习率 e p s l o n epslon epslon , 来感受梯度下降法的实际效果,当然也可以改变函数 f ( x ) f (x) f(x)。
2.5 牛顿法
梯度下降法是根据函数的一阶泰勒展开式推导的,能不能用二阶泰勒展开式呢? 答案是肯定的,这就是牛顿法。先从最简单的一元函数二阶泰勒展开式开始:


2.6 机器学习模型统一结构
机器学习包括3 个部分:
- 参数化的映射模型,将原始特征属性映射为类别分值向量;
- 损失函数,根据类别分值向量和训练集标签的相符程度,衡量参数好坏;
- 最优化, 寻找最优参数,使损失函数值最小。
本书主要涉及的映射模型有线性模型、神经网络和卷积神经网络,讲解的损失函数为softmax 损失函数,并且介绍基于梯度下降法的误差反向传播优化方法。
2.7 正则化
正则化的目的是控制模型的学习容量,减弱过拟合的风险。不论是参数化的线性模型、神经网络和卷积神经网络等,还是无参数的决策树以及朴素贝叶斯等,机器学习模型均存在过拟合现象。过拟合的外在表现形式是: 模型在训练集上的准确率明显高于在测试集上的准确率,即模型对训练集学得比较好,而测试集学得比较差。所以在实践中,经常利用这个性质来判断模型是否发生过拟合,如果过拟合,就需要增加正则化强度。
举个例子,现在要拟合平面上的3 个点,而二次函数能恰好拟合这3 个点,所以这个任务的理论容量只需二次函数。假设现在用三次函数进行拟合,显然三次函数也能完美拟合这3 个点。但是存在一个很严重的问题:解不唯一,即存在无穷个三次函数能完美拟合这3 个点。对于学习任务来说,如果模型存在多种可能的解,则说明模型的学习容量过高了。我们到底该选择哪一个解,这个解相比其他解的优势在哪里呢? 这个问题目前难以回答,普遍采用的原则是“奥卡姆剃刀” 。它是一种常用的自然科学研究中最基本的原则,即“当有多个假设与观察一致时,选择最简单的那个”,简单就是美。如果采用这个原则,那么对于三次函数, 哪种形式更简单呢?这显然不存在一个简单答案,需借助其他机制才能解决。假设认为简单的三次函数就是系数的平方和最小,即系数的2 范数最小,则我们就能从无穷个三次函数中选择一个最“合理”的函数。这个额外的对系数2 范数最小化的要求,就是我们对模型的偏好,也就是L2 正则化。所以,正则化可以看作我们对模型的偏好。如果偏好设置合理(符合样本真实规律),就能选到更好的解。除了系数的平方和最小,还可以要求系数的绝对值之和最小,这就是l 范数, L1 正则化;要求系数不为0 的数量最少,
这就是0 范数, L0 正则化。这3 种范数对应3 种正则化技术,是最常见的正则化技术。对于上面三次函数拟合问题,应该是0 范数偏好最合理,因为这会使三次项系数会优化为0 ,求得的最优函数就是二次函数。
再次强调,在实践中, 一般采用容量大的模型进行学习,然后通过正则化来控制过拟合。通过上面的例子可以看出,容量大的模型存在更多的可能解。通过梯度下降法能比较容易找到这些解,然后通过正则化偏好选择其中一个。相比之下,容量小的模型的解可能很少,因此要找到质量高的解很难。
增加模型容量很简单。对于神经网络和卷积网络,只需增加深度或宽度,我们一般优先增加深度。
2.7.1 范数正则化
对于生活中的实际问题,我们很难知道理想模型的形式,往往不能判断哪种范数更好,因此,实际中最常用的是L2 正则化技术。

为了使读者对范数正则化有一定的感性和理性认识,我们对损失函数进行简化分析。假设只有一个权重,数据损失在局部可近似为二次曲线(泰勒展开)。



综上分析,范数正则化后,最优权重会受到影响,即重要权重向0 靠近,不重要权重变为或趋近0。总之,权重的绝对值都会变小。可以说,范数正则化偏好小的权重,认为小权重的模型更简单。因为正则化强度越大(A 越大),最优权重受到的影响越大,所以数据损失部分会变大。
需要注意的是,与权重不同,偏置不需要正则化,因为偏置不与特征相乘,不能控制特征的影响强度。












