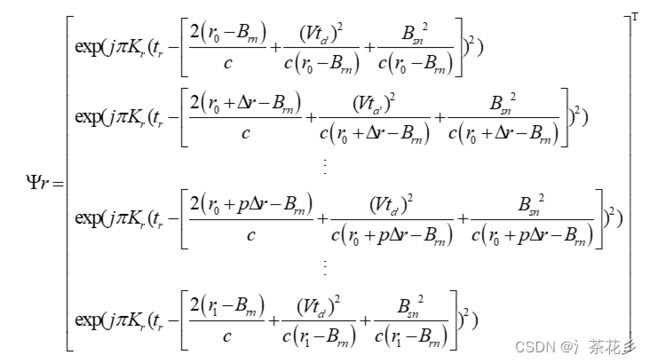SAR成像系列：【8】合成孔径雷达（SAR）成像算法-压缩感知（Compressed Sensing，CS）成像算法（附Matlab代码）
压缩感知（Compressed Sensing，CS）该理论指出：对于满足约束等距条件（Restricted Isometry Property，RIP）的稀疏或可压缩信号，通过低于（甚至远低于）Nyquist标准对其采样，就可足够精确地恢复出原始信号。自2007年莱斯大学的Baraniuk R等人首次将压缩感知引入高分辨雷达，压缩感知理论在雷达成像中的应用受到越来越多的关注.
SAR压缩感知成像既可在时域完成，也可在频域完成，这篇文章介绍一种时域压缩感知成像算法。
(1)压缩感知原理
信号的稀疏化、压缩测量和精确重构是构成压缩感知理论框架的主要部分。压缩感知技术对信号进行重构时，先对高维的稀疏信号进行非相关编码测量，实现采样和压缩两个步骤，然后在恢复信号时利用重构算法同时实现信号的解压与重建，大大降低测量系统的复杂度。
假定一个尺度为的一维信号
，稀疏度为
（即信号中有个不是零的值），
为
的二维矩阵（其中，
），
表示的是尺度为
的信号测量值。测量矩阵可以看作是M个传感器对信号进行的N点采样。则
其中，
表示为传感矩阵，为稀疏基矩阵。
通过求解上式的欠定方程，可以很大概率的求解出
的逼近值
，再利用
恢复出原始信号的逼近值，求解过程的图形表示如下图 所示。
根据上图，对信号的稀疏化、压缩测量和精确重构分别说明如下：
①信号的稀疏化
信号的稀疏表示是为了得到信号更为简洁和直接的表示方式，对于一般自然的信号本身很难保证稀疏性，需要一个正交稀疏基、过完备字典或自适应字典对信号进行稀疏化。即存在一组![\Phi ^{T}=[\Phi _{1},\Phi _{2},\Phi _{3},...,\Phi _{M}]](http://img.e-com-net.com/image/info8/4da946da00464e61b218fb37eb1d5693.gif){kind=small}
可以对尺度为
的信号线性分解。
②压缩测量
对信号进行压缩测量的物理意义可以理解为利用个传感器对维的原始信号进行观测，得到传感器的测量值
，采用最优化方法能够从观测值中重构出原始信号。通常，为了得到正确的测量值，需要测量矩阵和稀疏基
互不相关。其中，测量矩阵参与到压缩感知的整个过程，它的选择关系到信号压缩程度和重构精度。对于可压缩信号
，如果有满足上式就说明具备约束等距条件（RIP），那么通过
次采样便可将的个最大值精确重构，RIP条件等价于和不相关。对于测量矩阵，常见的有高斯矩阵、伯努利矩阵和傅里叶矩阵等。
③精确重构
信号的精确重构是压缩传感理论的灵魂，其算法主要有贪婪算法，如正交匹配追踪算法（Orthogonal Matching Pursuit，OMP）；凸松弛算法，如梯度投影算法（Gradient Projection for Sparse Reconstruction，GPSR）；以及它们的改进算法]等。
贪婪算法可描述为一种利用最小二乘不断迭代的算法，效率较高，但是其重构精度和抗噪性能有待提高。
凸松弛算法则是将病态求解范数问题转化为求解范数问题。转化为
考虑到误差影响，可写为
通过梯度投影法求解上式，得到
![\hat{S}=arg \underset{s}{min}[\left \| Y-\Theta S \right \|_{2}^{2}+\lambda_{k}\left \| S \right \|_{1}]](http://img.e-com-net.com/image/info8/9409dcf338ee4d5b8a63064a9953c7f2.gif){kind=small}
其中，
是与观测向量维数及噪声水平有关的拉格朗日算子。
根据压缩感知理论，要实现稀疏采样信号的完美重构，被采样信号必须满足稀疏性条件。SAR在成像时，若场景中任一距离门或方位门中强散射点的个数远小于与的散射点总数时，场景被认为是稀疏的。与经典的二维匹配滤波算法相同，基于压缩感知的二维重构也可分解为距离重构和方位重构两个过程。
(2)距离向重构
对于地面稀疏场景，设距离向分辨率为Δr，雷达在距离向的照射范围为[r0, r1]，每个距离单元内的散射中心可以表示为
![\alpha ^{T}=[\alpha_{1},\alpha_{2},...,\alpha_{P}]](http://img.e-com-net.com/image/info8/61a7b8adec57427695c87db3dab9c173.gif){kind=small}
其中，P表示距离照射范围内的距离门个数，
。
可写为
其中，
.因此距离向稀疏基（也叫稀疏字典）可构建为
稀疏基中加入了卫星基线B(Br，Ba，Bs)则回波信号可写为
因此，满足稀疏条件的
可通过压缩感知重构算法精确重构。的重构过程可看做是回波信号的距离压缩过程。
(3)方位向重构
距离向聚焦完成后，可在时域进行距离徙动矫正，得到的信号可表示为
带入
得
其中，
为距离重构后的单位冲激函数。这里的ta维数取决于合成孔径时间和雷达发射信号的PRF。一般地，合成孔径长度与雷达参数和雷达距地高度有关，在一个确定的雷达系统中可看做一个定值；因此，ta的维数仅取决于方位的采样频率，即雷达的PRF。根据压缩感知的特性(在满足稀疏性条件下，利用很少的采样实现信号的精确重构)，对稀疏场景成像时，通过降低雷达的PRF不仅可以大大降低原始回波的数据量，而且能够实现方位信号的精确重构，即方位聚焦。
与距离向重构过程相似，设方位向需要重构的分辨率为Δx，构建方位向稀疏基如下
其中，L为方位向分辨单元的个数，
为主星到场景中心的参考距离。这里需要注意的是：在精确成像时，可根据所处理的每一距离门信号，对方位向稀疏基进行修改，如在重构第p个距离门信号时，此时的方位向稀疏基写为
显然，对每一个距离门构建不同的方位向稀疏基，会增加算法的计算量。通常，可根据成像要求和场景测绘带宽对距离门进行分组，然后为每一组距离门分配一个相匹配的方位向稀疏基，以求达到成像精度和计算量之间的一个平衡。
(4)算法仿真
仿真参数如下表所示：
| 载频 | 5.3 GHz |
| 平台高度 | 800 Km |
| 平台速度 | 7100 m/s |
| 场景中心距 | 890 Km |
| 发射带宽 | 30 MHz |
| 脉宽 | 30 us |
| 天线孔径 | 10 m |
根据星载多基线SAR的系统参数，当下视角为48°时，雷达的多普勒带宽为1490Hz。根据Nyquist采样定理：复信号的Nyquist采样率与信号带宽相等，所以基于傅里叶变换的方位无模糊压缩所需的PRF应大于1490Hz。先进行RD成像，中PRF取1500Hz。成像结果如下。
RD算法距离压缩结果：
RD算法方位压缩成像结果：
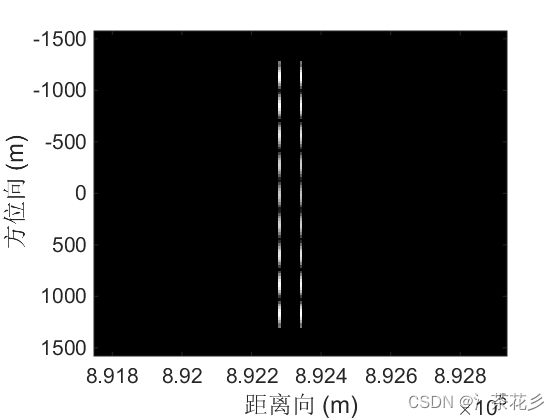
下面给出的是压缩感知成像结果，为了验证低采样率的完美重构效果，此时的PRF为150Hz。
压缩感知距离向重构结果：
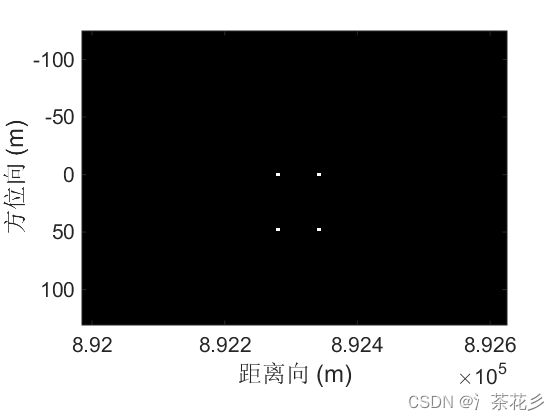
压缩感知方位向重构成像结果：
Matlab代码：
clc;
clear;
close all;
C=3e8; %光速
%星载SAR
disp('Spaceborne SAR')
%%雷达参数
Fc=5.3e9; %载频 C波段
lambda=C/Fc; %波长
%%轨道参数
V=7000; %SAR速度
H=800e3; %SAR的距离向距离 800km
%Rc=700000;
%%目标区域
theta=26.288/180*pi; %俯仰角θ(下视角)
Xmin=-200; %目标区的方位向范围[Xmin,Xmax]
Xmax=200;
Yc=H*tan(theta);
R0=H/cos(theta);
Y0=1000; %地距向成像范围[Yc-Y0,Yc+Y0]
%%天线参数
D=10; %SAR 方位向天线长度
Lsar=0.886*lambda*R0/D; %SAR 合成孔径长度
Tsar=Lsar/V;
%%快时间域参数
Tr=40e-6; %脉冲持续时间
Br=30e6; %线性调频信号调频率带宽 30MHz
Kr=Br/Tr; %调频率
sq_ang=0; % 正侧视 side-looking
Fsr=1.2*Br; %快时间采样率 1.2倍带宽
dt=1/Fsr; %快时间域采样步长 %SAR 合成孔径时间
%%慢时间域参数
Ka=-2*V^2/lambda/R0; %doppler 调频率
Ba=abs(Ka*Tsar); %doppler 调频带宽
PRF=200;
%PRF=0.8*Ba; %脉冲重复频率
PRT=1/PRF; %脉冲重复间隔
ds=PRT; %慢时间域采样步长
Nslow=ceil((Xmax-Xmin+Lsar)/V/ds); %慢时间域采样数
%Nslow=2^nextpow2(Nslow); %写成2的指数 for fft
sn=linspace((Xmin-Lsar/2)/V,(Xmax+Lsar/2)/V,Nslow); %慢时间域离散时间序列
Rmin=sqrt(H^2+(Yc-Y0)^2);
%Rmax=sqrt((Yc+Y0)^2+H^2); %SAR与一个孔径测绘带的最长距离
Rmax=sqrt(H^2+(Yc+Y0)^2);
Nfast=ceil(2*(Rmax-Rmin)/C/dt+Tr/dt); %快时间域的采样数
tfast=linspace(2*Rmin/C-Tr/2,2*Rmax/C+Tr/2,Nfast); %快时间域的离散时间序列
r=tfast*C/2;%距离向的距离序列
%%采样分辨率
DR=C*dt/2; %距离向分辨率
DX=V*ds; %方位向分辨率
%% 卫星参数
% %h=linspace(0,200,1);%高度向的均匀序列 基线范围为200
%卫星高度向的参数 基线长度
sN=4;%4颗卫星
Ba=0
Br=0;%先设置距离向基线为零
%Br=[0;330;104;270];
Bs=0;%相当于Bs
%% 目标参数
Targets;
K=Ntarget; %目标个数
N=Nslow; %慢时间域向量长度（即采样个数）
M=Nfast; %快时间域向量长度
T=Ptarget; %目标参数
%%生成回波信号
Srnm=zeros(N,M,sN);
for i=1:1:sN
for k=1:1:K
sigma=T(k,4);
Dslow=sn*V-T(k,1); %SAR与目标方位向距离形成的序列
R=sqrt(Dslow.^2+(T(k,2)-Br(i))^2+(Bs(i)-T(k,3))^2); %生成径向距离序列 加入距离向基线
tau=2*R/C; %生成径向距离延迟序列
Dfast=ones(N,1)*tfast-tau'*ones(1,M); %生成t-tao矩阵
phase=pi*Kr*Dfast.^2-(4*pi/lambda)*(R'*ones(1,M)); %回波相位矩阵
Srnm(:,:,i)=Srnm(:,:,i)+sigma*exp(j*phase).*(abs(Dfast)<=Tr/2).*((abs(Dslow)<=Lsar/2)'*ones(1,M));
end
end
%显示回波信号
%% 压缩感知二维成像
%CS_Image_2DMatrix=zeros(N,M,sN);%初始化压缩感知成像矩阵
k = 1；
Srnm1=awgn(Srnm(:,:,k),15); %取出单个雷达的信号回波(15dB 噪声)
%%距离向压缩感知
%距离分块
RR=R0-70*DR:DR:R0+70*DR;%根据距离向成像区域的大小分块
size_RR=size(RR,2);
%构造稀疏基
PsiR=zeros(Nfast,size_RR);%初始化稀疏基
for ii=1:size_RR
RR_index=RR(ii);
Tr_temp=tfast-2*RR_index/C;
PsiR_temp=Tr_temp.*(abs(Tr_temp)<=Tr/2);
PsiR(:,ii)=exp(j*pi*Kr*PsiR_temp.^2);
end
Ky=2*N1;%稀疏度 稀疏度的大小影响成像的能量集中程度
%%距离向用CS进行脉冲压缩
Srnm1=Srnm1.';%转置为了重构
%hat_y=zeros(Nslow,Nfast);%初始化重构矩阵
%omp重构
for i1=1:Nslow
hat_y(i1,:)=omp(Srnm1(:,i1),PsiR,Ky,0.5);
% hat_y(i1,:)=cs_iht(Srnm1(:,i1),Psi,Nfast,Ky);
end
figure;
colormap(gray);
imagesc(abs(hat_y));
title('距离向用压缩感知技术重构结果');
%%方位向成像
%%方位向用压缩感知的方法
%方法1 按列错位构建稀疏基
ta=sn-Xmin/V;%场景成像区间内慢时间序列
%ta=ta.*(abs(ta)
Refa=exp(j*pi*Ka_temp*ta.^2).*(abs(ta)
Nta=size(Refa);%基准信号长度
Nta=Nta(2);%
% Refa=-exp(j*pi*Ka*tma.^2);
PsiA=zeros(Nslow+Nta,Nslow);%初始化稀疏基
详细代码参考：
(46条消息) 合成孔径雷达（SAR）压缩感知（CS）二维成像Matlab代码。-行业报告文档类资源-CSDN文库