【NLP学习笔记】One-hot encoding:独热编码
一、存在问题
在机器学习算法中,特征并不总是连续值,常会遇到分类特征是离散的、无序的。例如:性别有男、女,城市有北京,上海,深圳等。
离散特征的编码分为两种情况:
- 离散特征的取值之间没有大小的意义,比如color:[red,blue],那么就使用one-hot编码
- 离散特征的取值有大小的意义,比如size:[X,XL,XXL],那么就使用数值的映射{X:1,XL:2,XXL:3}
性别特征:[“男”,“女”] = [ 0,1 ]
地区特征:[“北京”,"上海,“深圳”] = [ 0,1,2 ]
工作特征:[“演员”,“厨师”,“公务员”,“工程师”,“律师”] = [ 0,1,2,3,4 ]
比如,样本(女,北京,工程师)表示为[1,0,3],但是,这样的特征处理并不能直接放入机器学习算法中,因为,分类器通常默认数据是连续且有序。但是,按照我们上述的表示,数字并不是有序的,而是随机分配的。
解决这类问题,一种解决方法是采用独热编码(One-Hot Encoding)。
二、什么是独热编码?
独热编码即 One-Hot 编码,又称一位有效编码,其方法是使用N位状态寄存器来对N个状态进行编码,每个状态都有它独立的寄存器位,并且在任意时候,其中只有一位有效。
- 即,只有一位是1,其余都是零值。
下面结合具体例子对独热编码进行阐述:
- 对六个状态进行编码: N = 6
自然顺序码为:000,001,010,011,100,101
独热编码则是:000001,000010,000100,001000,010000,100000
回顾文章开头的例子:按照 N 位状态寄存器来对 N 个状态进行编码的原理,结果如下:
- 性别特征:[“男”,“女”](这里N=2)
- 男 = [ 1 0 ]
- 女 = [ 0 1 ]
- 地区特征:[“北京”,"上海,“深圳”](这里N=3):
- 北京 = [ 1 0 0 ]
- 上海 = [ 0 1 0 ]
- 深圳 = [ 0 0 1 ]
- 工作特征:[“演员”,“厨师”,“公务员”,“工程师”,“律师”](这里N=5):
- 演 员 = [ 1 0 0 0 0 ]
- 厨 师 = [ 0 1 0 0 0 ]
- 公务员 = [ 0 0 1 0 0 ]
- 工程师 = [ 0 0 0 1 0 ]
- 律 师 = [ 0 0 0 0 1 ]
因此,当某个样本的特征是 [“女”,“上海”,“律师”] 的时候,独热编码(One-Hot Encoding)的结果为:
[0,1,0,1,0,0,0,0,0,1]
换言之:
- 对于每一个特征,如果它有m个可能值,那么经过独热编码后,就变成了m个二元特征(如成绩这个特征有好,中,差三个可能值,即 m = 3,变成 one-hot 就是 [100, 010, 001] )。
- 并且,这些特征互斥,每次只有一个激活(如成绩取值为 好时,one-hot 编码是 [100] )。
- 因此,数据会变成稀疏的。
这样做的好处主要有:
- 解决了分类器不好处理属性数据的问题
- 在一定程度上也起到了扩充特征的作用
三、为什么需要独热编码?
- 因为大部分算法是基于向量空间中的度量来进行计算的,为了使非偏序关系的变量取值不具有偏序性,并且到圆点是等距的。使用one-hot编码,将离散特征的取值扩展到了欧式空间,离散特征的某个取值就对应欧式空间的某个点。
- 将离散型特征使用one-hot编码,会让特征之间的距离计算更加合理。离散特征进行one-hot编码后,编码后的特征,其实每一维度的特征都可以看做是连续的特征。就可以跟对连续型特征的归一化方法一样,对每一维特征进行归一化。
- 连续型特征归一化的常用方法:
- Rescale bounded continuous features——线性放缩 [-1,1]
- Standardize all continuous features——放缩到均值为0,方差为1。
3.1 为什么要将 特征向量 映射到 欧式空间 ?
- 因为在回归、分类、聚类等机器学习算法中,特征之间距离的计算或相似度的计算是非常重要的。
- 而常用的距离或相似度的计算都是在欧式空间的相似度计算,计算余弦相似性,就是基于欧式空间的。
比如,上面的工作特征,属于离散型特征,共有五个可能取值,不使用独热编码(One-Hot Encoding)的话,其数字表示分别为:
[ 演 员,厨 师,公务员,工程师,律 师 ] = [ 0,1,2,3,4 ]
那么不同工作特征之间的距离为:
d(演 员,厨 师)= 1
d(厨 师,公务员)= 1
d(公务员,工程师)= 1
d(工程师,律 师)= 1
d(演 员,公务员)= 2
d(演 员,工程师)= 3
以此类推…
显然,使用这样的表示 计算出来的特征的距离是不合理。
那如果使用独热编码(One-Hot Encoding),则得到d(演员,厨师) = 1与d(演员,公务员)都是1。那么,两个工作之间的距离就都是sqrt(2)。即每两个工作之间的距离是一样的,显得更合理。
四、one-hot编码过程详解
说明:n维向量指的是 向量的元素个数为 n !!!
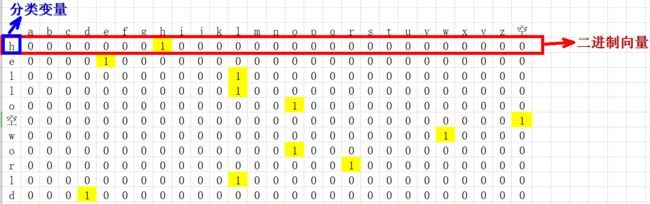
4.1 对 “hello world” 进行one-hot编码
- 确定要编码的对象–hello world,
- 确定分类变量的总类别数目–h e l l o 空格 w o r l d,共27种类别(26个小写字母 + 空格,);
- 以上问题就相当于,有11个样本,每个样本有27个特征,将其转化为二进制向量表示,
这里有一个前提,特征排列的顺序不同,对应的二进制向量亦不同(比如我把空格放在第一列和a放第一列,one-hot编码结果肯定是不同的)
因此我们必须要事先约定特征排列的顺序:
- 27种特征首先进行整数编码:a–0,b–1,c–2,…,z–25,空格–26
- 27种特征按照整数编码的大小从前往后排列
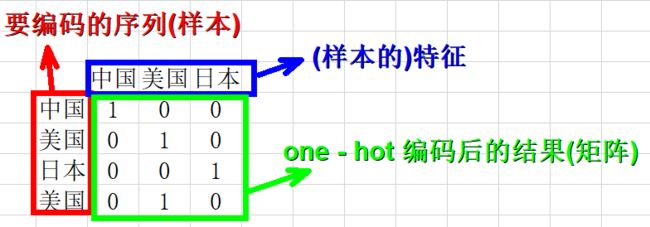
4.2 对[“中国”, “美国”, “日本”]进行one-hot编码
- 确定要编码的对象–[“中国”, “美国”, “日本”, “美国”],
- 确定分类变量–中国 美国 日本,共3种类别;
- 以上问题就相当于,有3个样本,每个样本有3个特征,将其转化为二进制向量表示。
我们首先进行特征的整数编码:中国–0,美国–1,日本–2,并将特征按照从小到大排列。得到one-hot编码如下:
[“中国”, “美国”, “日本”, “美国”] —> [[1,0,0], [0,1,0], [0,0,1], [0,1,0]]
五、优缺点
- 优点:独热编码解决了分类器不好处理属性数据的问题,在一定程度上也起到了扩充特征的作用。它的值只有0和1,不同的类型存储在垂直的空间。
- 缺点1:当类别的数量很多时,特征空间会变得非常大。在这种情况下,一般可以用PCA来减少维度。而且one hot encoding+PCA这种组合在实际中也非常有用。
- 缺点2:在文本特征表示上有些缺点就非常突出了。首先,它是一个词袋模型,不考虑词与词之间的顺序(文本中词的顺序信息也是很重要的);其次,它假设词与词相互独立(在大多数情况下,词与词是相互影响的);最后,它得到的特征是离散稀疏的。
六、如何解决 特征稀疏 引起的 维度灾难?
- Dristributed representation可以解决One hot representation的问题,它的思路是通过训练,将每个词都映射到一个较短的词向量上来。
- 所有的这些词向量就构成了向量空间,进而可以用普通的统计学的方法来研究词与词之间的关系。
- 这个较短的词向量维度是多大呢?这个一般需要我们在训练时自己来指定。
比如下图我们将词汇表里的词用"Royalty",“Masculinity”, "Femininity"和"Age"4个维度来表示,King这个词对应的词向量可能是(0.99,0.99,0.05,0.7)。当然在实际情况中,我们并不能对词向量的每个维度做一个很好的解释。
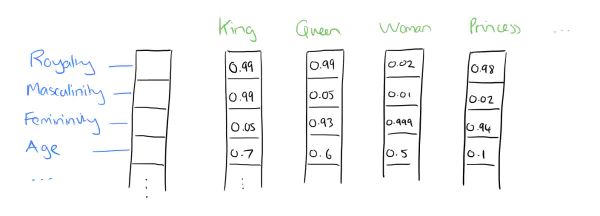
我们将 king 这个词从一个可能非常稀疏的向量所在的空间,映射到现在这个四维向量所在的空间,必须满足以下性质:
- 这个映射是单射;
- 映射之后的向量不会丢失原先向量所含的信息。
这个过程称为word embedding(词嵌入),即将高维词向量嵌入到一个低维空间。 如下图所示:

经过上述一系列的降维操作,有了用Dristributed representation表示的较短的词向量,我们就可以较容易的分析词之间的关系了。
七、使用独热编码的条件?
- 如果特征是离散的,并且不用独热编码就可以很合理的计算出距离,就没必要进行独热编码。(比如,离散特征共有1000个取值,分成两组是400和600,两个小组之间的距离有合适的定义,组内距离也有合适的定义,就没必要独热编码)
- 有些并不是基于向量空间度量的算法,例如基于树的算法,数值只是个类别符号,没有偏序关系,就不用进行独热编码。
- Tree Model不太需要one-hot编码: 对于决策树来说,one-hot的本质是增加树的深度。
- 如果原本的标签编码是有序的,就不必独热编码了,因为会丢失顺序信息。
- 用:独热编码用来解决类别型数据的离散值问题,
总的来说,如果one hot encoding的类别数目不太多,建议优先考虑。
八、使用归一化的条件?
- 需要: 基于参数的模型或基于距离的模型,都是要进行特征的归一化。
- 不需要:基于树的方法是不需要进行特征的归一化,例如随机森林,bagging 和 boosting等。
九、one-hot编码为什么可以解决类别型数据的离散值问题?
- 首先,one-hot编码是N位状态寄存器为N个状态进行编码的方式。
例如:高、中、低不可分,→ 用0 0 0 三位编码之后变得可分了,并且成为互相独立的事件 。
- 类似于 SVM,原本线性不可分的特征,经过project之后到高维之后变得可分了。
- GBDT处理高维稀疏矩阵的时候效果并不好,即使是低维的稀疏矩阵也未必比SVM好
十、Tree Model不需要one-hot编码
- 对于决策树来说,one-hot的本质是增加树的深度
- tree-model是在动态的过程中生成类似 One-Hot + Feature Crossing 的机制
- 一个特征或者多个特征最终转换成一个叶子节点作为编码 ,one-hot可以理解成三个独立事件
- 决策树是没有特征大小的概念的,只有特征处于他分布的哪一部分的概念
- one-hot可以解决线性可分问题,但是比不上label econding 。
- one-hot降维后的缺点: 降维前可以交叉的,降维后可能变得不能交叉 。
十一、one-hot coding和dummy encoding[7-8]
总结:
- 我们使用one-hot编码时,通常我们的模型不加bias项 或者 加上bias项然后使用正则化手段去约束参数;
- 当我们使用哑变量编码时,通常我们的模型都会加bias项,因为不加bias项会导致固有属性的丢失。
十二、如何使用独热编码?
- 由于one-hot编码太稀疏了,不要直接输入到神经网络里。
- 正确方法是初始化一个embedding矩阵E,维度是(d, n),其中n是类别数,在 hello world 这个例子中就是27,d是每个类别的embedding向量。然后用one-hot向量x乘E取出它对应的那一个embedding向量Ex,用这个随机向量输入到神经网络中。
参考资料
[1] 机器学习特征处理——独热编码(One-Hot Encoding)
[2] 数据预处理:独热编码(One-Hot Encoding)和 LabelEncoder标签编码
[3] 通俗理解word2vec
[4] What are good ways to handle discrete and continuous inputs together?
[5] 机器学习:数据预处理之独热编码(One-Hot)
[6] 详解one-hot编码
[7] 关于One-hot编码的一些整理及用途[转载+整理]
[8] 离散型特征编码方式:one-hot与哑变量*
[9] [Word Embedding系列] one-hot 编码
[10] 第一个回答:one-hot编码之后如何作为预测层的输入?
[11] 「周末AI课堂」理解词嵌入(理论篇)
[12] one-hot 编码 (one-hot encoding)