数学建模2019B “同心协力”策略研究
第一问
1.球的运动
两个假设条件:一、忽略阻力。二、视鼓面为平面。
设 z b ( t ) z_b(t) zb(t)为球在 t t t时刻的位置、 v b 1 v_{b1} vb1为球的初始速度、 m b m_b mb、 m d m_d md分别为球与鼓的质量。
根据牛顿第二定理和球的初始条件,可联立方程组:
{ m b d 2 z b d t 2 = − m b g z b ( 0 ) = 0 z b ′ ( 0 ) = v b 1 (1) \left\{ \begin{aligned} m_b\frac{d^2z_b}{dt^2} = -m_bg\\ z_b(0) = 0\\ z_b'(0) = v_{b1} \end{aligned} \right.\tag{1} ⎩ ⎨ ⎧mbdt2d2zb=−mbgzb(0)=0zb′(0)=vb1(1)
解得:
{ z b ( t ) = v b 1 − 1 2 g t 2 z b ′ ( t ) = v b 1 − g t (2) \left\{ \begin{aligned} z_b(t) = v_{b1} - \frac{1}{2}gt^2\\ z_b'(t) = v_{b1} - gt \end{aligned} \right.\tag{2} ⎩ ⎨ ⎧zb(t)=vb1−21gt2zb′(t)=vb1−gt(2)
到达最高点所需的时间为: t b = v b 1 g t_b = \frac{v_{b1}}{g} tb=gvb1
到达的最大高度为: h b = v b 1 2 2 g h_b=\frac{v_{b1}^2}{2g} hb=2gvb12
从给定高度 h b h_b hb处下落到鼓上并反弹后的速度为: v b 1 = 2 g h b v_{b1} = \sqrt{2gh_b} vb1=2ghb
到达鼓面时的速度为: v b 0 = − v b 1 = − 2 g h b v_{b0} = -v_{b1} = -\sqrt{2gh_b} vb0=−vb1=−2ghb
2.鼓与球的碰撞
设 m b m_b mb、 v b 0 v_{b0} vb0、 v b 1 v_{b1} vb1、 m d m_d md、 v d 0 v_{d0} vd0、 v d 1 v_{d1} vd1分别为球的质量、球与鼓碰撞前的球的速度、球与鼓碰撞后球的速度、鼓的质量、球与鼓碰撞前的鼓的速度、球与鼓碰撞后鼓的速度。
根据动量守恒与动能守恒定理可列出以下方程:
{ m b v b 0 + m d v d 0 = m b v b 1 + m d v d 1 1 2 m b v b 0 2 + 1 2 m d v d 0 2 = 1 2 m b v b 1 2 + 1 2 m d v d 1 2 (3) \left\{ \begin{aligned} m_bv_{b0} + m_dv_{d0} = m_bv_{b1} + m_dv_{d1}\\ \frac{1}{2}m_bv_{b0}^2+\frac{1}{2}m_dv_{d0}^2 = \frac{1}{2}m_bv_{b1}^2+\frac{1}{2}m_dv_{d1}^2 \end{aligned} \right.\tag{3} ⎩ ⎨ ⎧mbvb0+mdvd0=mbvb1+mdvd121mbvb02+21mdvd02=21mbvb12+21mdvd12(3)
解得:
{ v b 1 = ( m b − m d ) v b 0 + 2 m d v d 0 m b + m d v d 1 = ( m d − m b ) v d 0 + 2 m b v b 0 m b + m d (4) \left\{ \begin{aligned} v_{b1} = \frac{(m_b - m_d)v_{b0} + 2m_dv_{d0}}{m_b + m_d}\\ v_{d1} = \frac{(m_d - m_b)v_{d0} + 2m_bv_{b0}}{m_b + m_d} \end{aligned} \right.\tag{4} ⎩ ⎨ ⎧vb1=mb+md(mb−md)vb0+2mdvd0vd1=mb+md(md−mb)vd0+2mbvb0(4)
已知当球从 h b h_b hb处落下时,球碰撞前速度为: v b 0 = 2 g h b v_{b0} = \sqrt{2gh_b} vb0=2ghb
要让球碰撞后反弹至原来的高度,鼓碰撞前的速度应为: v d 0 = m b m d ⋅ 2 g h v_{d0} = \frac{m_b}{m_d}\cdot \sqrt{2gh} vd0=mdmb⋅2gh
3.鼓的运动
记共有 n n n个队员,第 j j j个队员顺着绳子的拉力为 F j F_j Fj,其垂直分量为 F v j F_{vj} Fvj、水平分量为 F h j F_{hj} Fhj。
我们假设每个队员拉力大小方向都一样。
则:
∑ i = 1 n F h j = 0 \sum_{i=1}^nF_{hj} = 0 i=1∑nFhj=0
记 F v = F v j F_v = F_{vj} Fv=Fvj
则所有队员的拉力和为 n F v nFv nFv
记 z d ( t ) z_d(t) zd(t)为 t t t时刻鼓的位置、 − h d -h_d −hd为鼓初始位置。
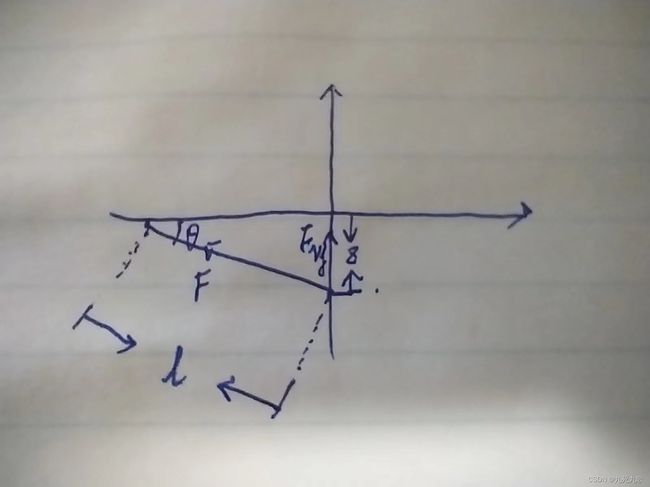
由上图可知: F v = F sin θ = − F z l F_v = F\sin{\theta}=-F\frac{z}{l} Fv=Fsinθ=−Flz
再根据牛顿第二定理和鼓运动的初始条件即可联立以下方程组:
{ m d d 2 z d d t 2 = n F v − m d g z d ( 0 ) = − h d z d ′ ( 0 ) = 0 (5) \left\{ \begin{aligned} m_d\frac{d^2z_d}{dt^2} = nF_v - m_dg\\ z_d(0) = -h_d\\ z_d'(0) = 0 \end{aligned} \right.\tag{5} ⎩ ⎨ ⎧mddt2d2zd=nFv−mdgzd(0)=−hdzd′(0)=0(5)
解得:
{ z d ( t ) = ( l g m d n F − h d ) cos ( n F m d l t ) − l g m d n F z d ′ ( t ) = n F m d l ( h d − l g m d n F ) s i n ( n F m d l t ) (5) \left\{ \begin{aligned} z_d(t) = (\frac{lgm_d}{nF} - h_d)\cos(\sqrt{\frac{nF}{m_dl}}t) - \frac{lgm_d}{nF}\\ z_d'(t) = \sqrt{\frac{nF}{m_dl}}(h_d - \frac{lgm_d}{nF})sin(\sqrt{\frac{nF}{m_dl}}t) \end{aligned} \right.\tag{5} ⎩ ⎨ ⎧zd(t)=(nFlgmd−hd)cos(mdlnFt)−nFlgmdzd′(t)=mdlnF(hd−nFlgmd)sin(mdlnFt)(5)
当 t d = π 2 m d l n F t_d = \frac{\pi}{2}\sqrt{\frac{m_dl}{nF}} td=2πnFmdl时,有: v m a x = n F m d l ( h d − l g m d n F ) v_{max} = \sqrt{\frac{nF}{m_dl}}(h_d - \frac{lgm_d}{nF}) vmax=mdlnF(hd−nFlgmd)
鼓的最大速度应等于球与鼓碰撞前的速度、以 h d h_d hd为未知数,求解方程:
n F m d l ( h d − l g m d n F ) = v d 0 (7) \sqrt{\frac{nF}{m_dl}}(h_d - \frac{lgm_d}{nF}) = v_{d0}\tag{7} mdlnF(hd−nFlgmd)=vd0(7)
解得:
h d = m d l n F v d 0 + l g m d n F (8) h_d = \sqrt{\frac{m_dl}{nF}}v_{d0} + \frac{lgm_d}{nF}\tag{8} hd=nFmdlvd0+nFlgmd(8)
联立方程:
h d = m d l n F v d 0 + l g m d n F = 2 t d π v d 0 + 4 g t d 2 π 2 (9) h_d = \sqrt{\frac{m_dl}{nF}}v_{d0} + \frac{lgm_d}{nF} = \frac{2t_d}{\pi}v_{d0} + \frac{4gt_d^2}{\pi^2}\tag{9} hd=nFmdlvd0+nFlgmd=π2tdvd0+π24gtd2(9)
视所有队员看到球反弹至最高点时同时发力,可知: t d = t b t_d=t_b td=tb
方程结果为:
F = π 2 l g m d 8 n h b F = \frac{\pi^2lgm_d}{8nh_b} F=8nhbπ2lgmd
由题目代入相关数据 h b = 0.4 h_b = 0.4 hb=0.4、 n = 8 n = 8 n=8、 m d = 3.6 m_d = 3.6 md=3.6、 l = 2 l = 2 l=2。即可求出最终结果。
而用力时机为球反弹至最高点时、用力方向为顺着绳子用力、颠球高度为40cm