十大排序算法实现与总结(Java语言)
本文是对十大排序算法的总结:(冒泡排序、选择排序、插入排序、希尔排序、归并排序、堆排序、快速排序、计数排序、桶排序、基数排序)
目录
1.冒泡排序
2.选择排序
3.插入排序
4.希尔排序
5.归并排序
6.堆排序
7.快速排序
8. 计数排序
9.桶排序
10 基数排序
1.冒泡排序
基本思想:每一轮两两比较相邻记录的关键字,如果反序则进行交换。基本实现代码如下:
public class BubbleSort {
public static void main(String[] args) {
// 这里以升序方式排列数组为例子。
int[] nums = new int[]{8,6,4,7,-2,1,12};
// 排序
sort(nums);
// 打印数组
for (int i = 0; i < nums.length; i++) {
System.out.print(nums[i] + " ");
}
}
public static void sort(int[] nums) {
// 外层循环代表冒泡轮数
for (int i = 0; i < nums.length; i++) {
// 内层循环则为两两比较,遇到反序则交换
for (int j = 1; j < nums.length; j++) {
if (nums[j - 1] > nums[j]) {
int temp = nums[j - 1];
nums[j - 1] = nums[j];
nums[j] = temp;
}
}
}
}
}
输入数组:
8 6 4 7 -2 1 12
运行结果:
-2 1 4 6 7 8 12
冒泡排序优化:如果某一轮没有发生交换,说明数组已经有序,可以提前结束循环:
public class BubbleSort2 {
public static void main(String[] args) {
// 这里以升序方式排列数组为例子。
int[] nums = new int[]{8,6,4,7,-2,1,12};
// 排序
sort(nums);
// 打印数组
for (int i = 0; i < nums.length; i++) {
System.out.print(nums[i] + " ");
}
}
public static void sort(int[] nums) {
// 设置一个变量标识当前轮是否发生交换
boolean flag = true;
// 外层循环代表冒泡轮数
for (int i = 0; i < nums.length; i++) {
// 每轮开始前,默认不会发生交换
flag = false;
// 内层循环则为两两比较,遇到反序则交换
for (int j = 1; j < nums.length; j++) {
if (nums[j - 1] > nums[j]) {
// 发生交换,将信号设置为true;
flag = true;
int temp = nums[j - 1];
nums[j - 1] = nums[j];
nums[j] = temp;
}
}
// 一轮结束,如果没有发生交换,则提前终止冒泡排序
if (!flag) {
break;
}
}
}
}
输入数组:
8 6 4 7 -2 1 12
运行结果:
-2 1 4 6 7 8 12
2.选择排序
基本思想:(以升序排序为例子)第一轮,找到数组中最小的元素,将它和数组的第一个元素交换位置,第二轮,在剩下的元素中继续寻找最小的元素,和数组的第二个元素交换位置,第三轮,在剩下的元素中继续寻找最小的元素,和数组的第三个元素交换位置。依次类推,直到整个数组排序完成。以下为代码实现:
public class SelectionSort {
public static void main(String[] args) {
// 这里以升序方式排列数组为例子。
int[] nums = new int[]{8,6,4,7,-2,1,12};
// 排序
sort(nums);
// 打印数组
for (int i = 0; i < nums.length; i++) {
System.out.print(nums[i] + " ");
}
}
public static void sort(int[] nums) {
// 外层循环代表每一轮,每一轮可以确定一个元素的位置
for (int i = 0; i < nums.length; i++) {
// 每一轮都从剩余元素中找到最小的元素
int minIndex = i;
for (int j = i + 1; j < nums.length; j++) {
if (nums[j] < nums[minIndex]) {
minIndex = j;
}
}
// 找到最小元素后,交换位置
int temp = nums[i];
nums[i] = nums[minIndex];
nums[minIndex] = temp;
}
}
}输入数组:
8 6 4 7 -2 1 12
运行结果:
-2 1 4 6 7 8 12
3.插入排序
基本思想:把数组中的数据分成两个区域,已排序区域和未排序区域,每次从未排序区域中拿出一个元素插入在已排序区域的合适位置上。(初始化的时候可以认为数组第一个元素在已排序区域,其余元素在未排序区域),实现代码如下:
public class InsertionSort {
public static void main(String[] args) {
// 这里以升序方式排列数组为例子。
int[] nums = new int[]{8,6,4,7,-2,1,12};
// 排序
sort(nums);
// 打印数组
for (int i = 0; i < nums.length; i++) {
System.out.print(nums[i] + " ");
}
}
public static void sort(int[] nums) {
// 初始默认第一个元素在有序区域,所以初始的有序区域为[0 ~ 0], 无序区域为[1 ~ nums.length - 1]
// 所以我们从无序区域的第一个位置开始,即 i = 1 开始
// 外层循环代表每一次拿一个元素
for (int i = 1; i < nums.length; i++) {
// 要插入的元素值
int value = nums[i];
// 从已排序的最后一个位置开始
int j = i - 1;
// 内层循环从后往前(已排序区域),找到合适的位置将元素插入
for (; j >= 0; j--) {
// j 位置元素大于 value
if (nums[j] > value) {
nums[j + 1] = nums[j];
} else { // 找到合适位置,跳出循环
break;
}
}
// 放在当前元素位置的后面(当前位置的元素是<=value,所以放在后面)
nums[j + 1] = value;
}
}
}输入数组:
8 6 4 7 -2 1 12
运行结果:
-2 1 4 6 7 8 12
4.希尔排序
基本思想: 先将整个待排元素序列分割成若干子序列(每相隔X个元素取一个元素组成的子序列,这里X被称为增量)分别进行插入排序,然后依次缩减X,待整个序列中的元素基本有序时,再对全体元素进行一次插入排序(X = 1)。
希尔排序一定程度上优化了插入排序,因为基本的插入排序每次只能将数据移动一位,而希尔排序让数据移动的步伐加大,一定程度上节省了挪动元素的时间。代码如下:
public class ShellSort {
public static void main(String[] args) {
// 这里以升序方式排列数组为例子。
int[] nums = new int[]{8,6,4,7,-2,1,12};
// 排序
sort(nums);
// 打印数组
for (int i = 0; i < nums.length; i++) {
System.out.print(nums[i] + " ");
}
}
public static void sort(int[] nums) {
// 获取数组长度
int len = nums.length;
// 增量X
int X = 1;
// 根据数组长度计算合适的初始增量
while (X < len) {
X = 3 * X + 1;
}
while (X > 0) {
// 子序列进行插入排序
// 取其中一个子序列[0 * X, 1 * X, 2 * X, ....] 为例,这里指的是数组的下标
// 已排序区间为[0 ~ 0], 未排序区间为[1 * X ~ ...], 所以下标从X开始
for (int i = X; i < len; i++) {
// 要插入的元素值
int value = nums[i];
// 从已排序区间的最后一个位置开始
int j = i - X;
for (; j >=0; j -= X) {
// j 位置元素大于 value, 将当前元素往后挪
if (nums[j] > value) {
nums[j + X] = nums[j];
} else { // 找到合适位置,跳出循环
break;
}
}
// 放在当前元素位置的后面(当前位置的元素是<=value,所以放在后面)
nums[j + X] = value;
}
// 缩小增量
X /= 3;
}
}
}输入数组:
8 6 4 7 -2 1 12
运行结果:
-2 1 4 6 7 8 12
5.归并排序
基本思想: 分治法,将数组分块,先将一个数组一分为二,得到的两个子数组再一分为二,得到四个数组,依次类推,直到分成单个元素,然后重新组装合并,单个元素合并成小数组,两个小数组合并成大数组,每次合并保证块内有序,直到最终合并完成则排序完毕。代码如下:
public class MergeSort {
public static void main(String[] args) {
// 这里以升序方式排列数组为例子。
int[] nums = new int[]{8,6,4,7,-2,1,12};
// 创建一个和原数组一样大的数组作为临时数组,用于存放需要两个需要合并子数组的数据
int[] tempNums = new int[nums.length];
// 排序
sort(nums, tempNums,0, nums.length - 1);
// 打印数组
for (int i = 0; i < nums.length; i++) {
System.out.print(nums[i] + " ");
}
}
/**
*
* @param nums 需要排序的数组
* @param tempNums 用于存放需要两个需要合并子数组的数据
* @param start 每块的起始位置索引
* @param end 每块的终止位置索引
*/
public static void sort(int[] nums, int[] tempNums, int start, int end) {
// 块内元素小于等于一个,结束划分
if (end <= start) {
return;
}
// 将数组一分为二, 先求出中间位置
int mid = start + (end - start) / 2; // 防止数据溢出,等价于 (start + end) / 2
// 分块
sort(nums, tempNums, start, mid);
sort(nums, tempNums, mid + 1, end);
// 合并
// 复制需要合并的数据
for (int i = start; i <= end; i++) {
tempNums[i] = nums[i];
}
// 左子数组的指针,初始指向左子数组的第一个位置
int left = start;
// 右子数组的指针,初始指向右子数组的第一个位置
int right = mid + 1;
// 保证两个子数组合并之后有序
for (int k = start; k <= end; k++) {
// 如果左指针指向左子数组的最后位置的下一个位置,代表左子数组已经排完
if (left > mid) {
// 剩下位置放右子数组的剩余元素即可
nums[k] = tempNums[right++];
} else if (right > end){// 如果右指针指向右子数组的最后位置的下一个位置,代表右子数组已经排完
// 剩下位置放左子数组的剩余元素即可
nums[k] = tempNums[left++];
} else if (tempNums[left] < tempNums[right]) { // 如果左子数组的当前位置元素更小
// 将左子数组元素放入
nums[k] = tempNums[left++];
} else { // 如果右子数组的当前位置元素更小
// 将右子数组元素放入
nums[k] = tempNums[right++];
}
}
}
}
输入数组:
8 6 4 7 -2 1 12
运行结果:
-2 1 4 6 7 8 12
6.堆排序
基本思想:利用堆这种数据结构来进行排序的算法,以升序排序数组为例,维护一个大顶堆(堆顶元素为当前最大元素),每次从堆中取出一个最大值,得到的就是最大值,放在数组的最后一个位置,取完后把堆重新构建一下,然后再取堆顶的元素,得到的就是第二大的元素,放在数组倒数第二个位置,这样反复的取,直到堆只剩一个元素,则数组完成排序。基本步骤可以总结为以下步骤
步骤一:构建初始堆,将待排序列构成一个大顶堆。(如果是降序排序,则构成一个小顶堆)
步骤二:将堆顶元素与堆尾元素交换,并断开(从待排序列中移除)堆尾元素。(取出一个最大值)
步骤三:重新构建堆。(调整为一个新的大顶堆)
重复步骤二和三。直到堆中只剩下一个元素。
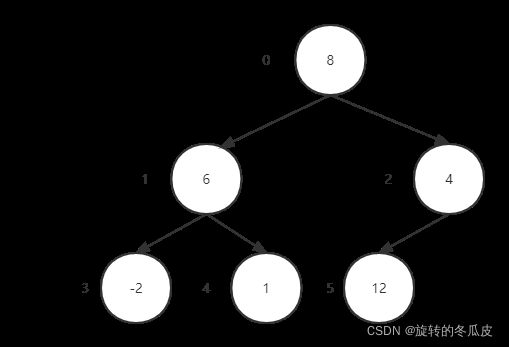
为了更好理解,我们以数组[8 6 4 -2 1 12]。首先是初始化堆,堆是一个树形结构,底层是一棵完全二叉树。而完全二叉树是一层一层按照进入的顺序排成的。所以,我们可以用数组来实现完全二叉树的结构,然后调整为堆。
数组实现完全二叉树结构,每一个节点i的左孩子的索引为2 * i + 1, 右孩子索引为2 * i + 2, 如图所示,节点中的值为元素值,旁边为对应在数组中的索引。
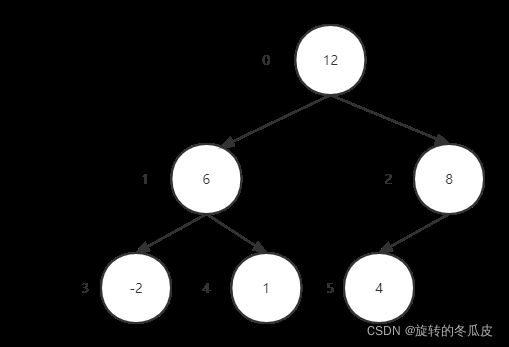
将完全二叉树树调整为大顶堆[12,6,8,-2,1,4]
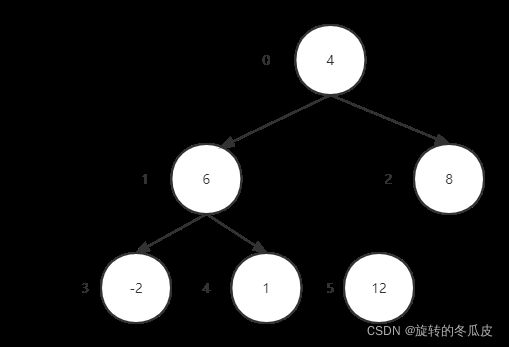
执行步骤二,取出堆顶元素(将堆顶元素与堆尾元素交换,并断开(从待排序列中移除)堆尾元素)
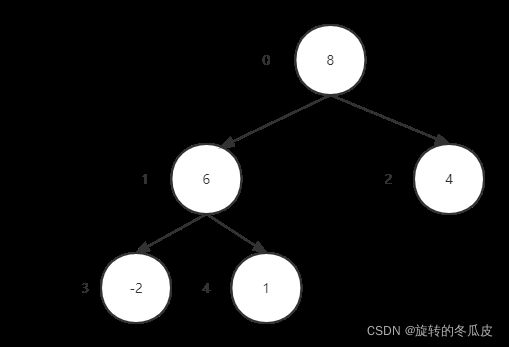
执行步骤三,重新构建堆(调整为一个新的大顶堆)【8,6,4,-2,1】,从堆顶元素开始下沉,让新的最大元素浮上来
重复步骤二和三,直到堆中只剩下一个元素。
以下为代码实现:
public class HeapSort {
public static void main(String[] args) {
// 这里以升序方式排列数组为例子。
int[] nums = new int[]{8,6,4,7,-2,1,12};
// 排序
sort(nums);
// 打印数组
for (int i = 0; i < nums.length; i++) {
System.out.print(nums[i] + " ");
}
}
public static void sort(int[] nums) {
// 获取数组长度
int len = nums.length;
// 初始化堆
buildHeap(nums, len);
// 每次从堆顶元素中取出一个元素,放到末尾
for (int i = len - 1; i > 0; i--) {
int temp = nums[0];
nums[0] = nums[i];
nums[i] = temp;
// 将末尾元素断开(只需将可见长度减一即可)
len--;
// 调整为一个新的大顶堆
adjustHeap(nums, 0, len);
}
}
public static void buildHeap(int[] nums, int len) {
// 调整好堆
for (int i = len / 2; i >= 0; i--) {
adjustHeap(nums, i, len);
}
}
/**
*
* @param nums 排序的数组
* @param index 需要调增的位置
* @param len 数组范围
*/
public static void adjustHeap(int[] nums, int index, int len) {
// 需要调整位置为父节点,查看两个子节点的值
int present = index;
// 获取左孩子索引
int leftChild = 2 * index + 1;
// 获取有孩子索引
int rightChild = 2 * index + 2;
// 如果左孩子存在且大于父节点, 标记父节点应该和左节点交换
if (leftChild < len && nums[leftChild] > nums[present]) {
present = leftChild;
}
// 如果左孩子存在且大于父节点, 标记父节点应该和右节点交换
if (rightChild < len && nums[rightChild] > nums[present]) {
present = rightChild;
}
// present != index 说明需要调换位置
if (present != index) {
int temp = nums[present];
nums[present] = nums[index];
nums[index] = temp;
// 继续向下调整位置
adjustHeap(nums, present, len);
}
}
}
输入数组:
8 6 4 -2 1 12
运行结果:
-2 1 4 6 8 12
7.快速排序
基本思想:每次从数组中选出一个基准值,把比基准值大的放一边,比基准值小的放在另外一边,然后再对两边边的两组数分别选出一个基准值,进行同样的操作,重复这个过程,直到最后都变成单个元素,则整个数组就成了有序的序列。以下为代码实现:
public class QuickSort {
public static void main(String[] args) {
// 这里以升序方式排列数组为例子。
int[] nums = new int[]{8,6,4,7,-2,1,12};
// 排序
sort(nums, 0, nums.length - 1);
// 打印数组
for (int i = 0; i < nums.length; i++) {
System.out.print(nums[i] + " ");
}
}
/**
*
* @param nums 数组
* @param start 起始位置
* @param end 终止位置
*/
public static void sort(int[] nums, int start, int end) {
// 如果元素个数小于等于一个,停止快速排序
if (start >= end) {
return;
}
// 左边扫描开始位置
int left = start;
// 右边开始扫描位置
int right = end;
// 设置一个基准值,默认采用最左边第一个元素的值作为基准值
int flagValue = nums[start];
while (left < right) {
// 从右边开始扫描,找到一个小于基准值的元素
while (left < right && nums[right] >= flagValue) {
right--;
}
if (left < right) {
// 找到后,放在左边
nums[left] = nums[right];
}
// 从左边开始扫描,找到一个大于基准值的元素
while (left < right && nums[left] < flagValue) {
left++;
}
if (left < right) {
// 找到后,放在右边
nums[right] = nums[left];
}
}
// 将基准值归位
nums[left] = flagValue;
// 对两个字数组分别做快速排序
sort(nums, start, left - 1);
sort(nums, left + 1, end);
}
}输入数组:
8 6 4 7 -2 1 12
运行结果:
-2 1 4 6 7 8 12
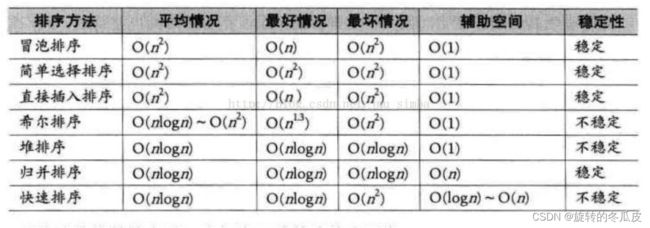
对于以上七种排序算法的时间复杂度、空间复杂度以及稳定性可以参考下图,下图为大学教材数据结构与算法中的一张总结表:
8. 计数排序
基本思想:计数排序是一种非基于比较的排序算法,利用空间换取时间,使用一个额外的数组B,其中这个额外数组的长度为原排序数组A最大元素值+1,额外数组B用于统计原排序数组中每个数字出现的次数(比如原排序数组中第i个元素值为A[i],则B[A[i]]值加1),依次按顺序读取这个额外数组即可完成排序。
举个例子:[8 6 4 7 5 5 12]
最大元素为12,则数组B的长度为13,依次统计每个元素出现的次数,得到以下数组B:
接着,我们只要按顺序读取这个数组即可完成排序[4,5,5,6,7,8,12].
以下为代码实现:
public class CountingSort {
public static void main(String[] args) {
// 这里以升序方式排列数组为例子。
int[] nums = new int[]{8,6,4,7,5,5,12};
// 排序
sort(nums);
// 打印数组
for (int i = 0; i < nums.length; i++) {
System.out.print(nums[i] + " ");
}
}
public static void sort(int[] nums) {
// 找到原排序数组的最大值
int maxValue = nums[0];
for (int i = 0; i < nums.length; i++) {
if (nums[i] > maxValue) {
maxValue = nums[i];
}
}
// 创建额外计数数组
int[] countNums = new int[maxValue + 1];
// 计数
for (int oneNum : nums) {
countNums[oneNum]++;
}
// 排序
int index = 0;
for (int i = 0; i < countNums.length; i++) {
if (countNums[i] > 0) {
int account = countNums[i];
while (account > 0) {
nums[index++] = i;
account--;
}
}
}
}
}输入数组:
8 6 4 7 5 5 12
运行结果:
4 5 5 6 7 8 12
计数排序的时间复杂度为O(n+m),m指的是数据量,在数据量较小的情况下,计数排序算法的时间复杂度约等于O(n),快于任何比较型的排序算法。但是,如果数据量比较大,且数值比较大时,比如为【453,677,888,525,755,322,123】,需要开辟的额外数组空间将会比较大。所以有了下面的桶排序。
9.桶排序
基本思想:将要排的数据分到多个有序的桶里,每个桶里的数据再单独排序,再把每个桶的数据依次取出,即可完成排序。
以上面的【453,677,888,525,275,322,123】为例子
创建4个桶,每个桶可以放200个不同的元素,将原数组数据放入到对应的桶中
然后每个桶再单独排序
依次读出每个桶的数据,即可完成排序[123,275,322,453,525,677,888].
关于创建桶的问题:
创建桶的前提是我们需要先确定桶的数量以及每个桶所能放置不同数值元素的个数
备注一下:为什么确定桶数量很重要?
(1)桶太少,所有数据都放在同一个桶里,则桶排序失去意义。
(2)桶过多,有的桶里可能没有数据,浪费存储空间。
一种推荐的确定桶数量的方法:
(1)找确定出数组所在范围min~max
(2)桶数量 = (max - min)/ 希望每个桶所能放置不同数值元素的个数 + 1
以下为代码实现:
public class BucketSort {
public static void main(String[] args) {
// 这里以升序方式排列数组为例子。
int[] nums = new int[]{453,677,888,525,275,322,123};
// 排序
sort(nums);
// 打印数组
for (int i = 0; i < nums.length; i++) {
System.out.print(nums[i] + " ");
}
}
public static void sort(int[] nums) {
// 获取数据范围
int maxValue = nums[0];
int minValue = nums[0];
for (int oneNum : nums) {
if (oneNum > maxValue) {
maxValue = oneNum;
}
if (oneNum < minValue) {
minValue = oneNum;
}
}
// 设置每个桶可以放置的不同元素个数
int bucketSize = 200;
// 计算桶数量
int bucketNum = (maxValue - minValue) / bucketSize + 1;
// 创建桶列表
List> bucketList = new ArrayList();
// 初始化桶列表
for (int i = 0; i < bucketNum; i++) {
List oneBucket = new ArrayList();
bucketList.add(oneBucket);
}
// 将原数组数据放入对应的桶中
for (int oneNum : nums) {
// 计算桶应该放在哪个桶
int bucketIndex = (oneNum - minValue) / bucketSize;
bucketList.get(bucketIndex).add(oneNum);
}
// 对桶内元素进行排序(桶内使用什么排序算法这里不做要求,这里为了好理解,直接采用库函数进行排序)
for (List oneBucket : bucketList) {
// 元素多于一个,则进行排序(只有一个元素或者空桶不用排)
if (oneBucket.size() > 1) {
Collections.sort(oneBucket);
}
}
int index = 0;
// 依次取出数据,完成排序
for (List oneBucket : bucketList) {
// 桶里有元素则读取元素
if (oneBucket.size() > 0) {
for (Integer oneNum : oneBucket) {
nums[index++] = oneNum;
}
}
}
}
} 输入数组:
453 677 888 525 275 322 123
运行结果:
123 275 322 453 525 677 888
桶排序其实还可以进一步优化,将数据存储在位数组上,可以极大程度的节省空间。
10 基数排序
基本思想:是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。其可以看成是桶排序的扩展。排序顺序有两种,分别为
(1)MSD 从高位开始进行排序
(2)LSD 从低位开始进行排序
这里我选择LSD(从低位开始进行排序)来举例,我们假设待排序数组为[453,677,888,525,275 322,123].
步骤一:将每个数按照个位放入桶中,这里桶的个数为10,因为所排序的为10进制的数,每一位只有十种可能:
步骤二:将数按桶的顺序取出,完成一次排序,得到[322,123,453,275,525,677,888]
步骤三:将每个数按照十位放入桶中:
步骤四:将数按桶的顺序取出,完成一次排序,得到[123,322,453,525,275,677,888]
步骤五:将每个数按照百位放入桶中:
步骤六:将数按桶的顺序取出,排序,得到[123,275,322,453,525,677,888]
以下为代码实现:
public class RadixSort {
public static void main(String[] args) {
// 这里以升序方式排列数组为例子。
int[] nums = new int[]{453,677,888,525,275,322,123};
// 排序
sort(nums);
// 打印数组
for (int i = 0; i < nums.length; i++) {
System.out.print(nums[i] + " ");
}
}
public static void sort(int[] nums) {
// 获取最大的位个数,决定要进行几次排序
int maxValue = nums[0];
for (int i = 1; i < nums.length; i++) {
if (nums[i] > maxValue) {
maxValue = nums[i];
}
}
// 计算出有多少位
int digits = 0;
while (maxValue > 0) {
maxValue /= 10;
digits++;
}
// 创建好桶
List> bucketList = new ArrayList>();
for (int i = 0; i < 10; i++) {
List oneBucket = new ArrayList();
bucketList.add(oneBucket);
}
// 从低位到高位排序
// temp1 和 temp2 用来取对应位的数字
int temp1 = 10;
int temp2 = 1;
while (digits > 0) {
// 按照每个数对应位的数字放入桶中
for (int oneNum : nums) {
int number = (oneNum % temp1) / temp2;
// 放入桶中
bucketList.get(number).add(oneNum);
}
// 按桶顺序取出数字
int index = 0;
for (List oneBucket : bucketList) {
// 桶若不为空,取出其中的数字
if (oneBucket.size() > 0) {
for (Integer oneNum : oneBucket) {
nums[index++] = oneNum;
}
// 取完后清空桶
oneBucket.clear();
}
}
// 取更高位进行下一步排序
temp1 *= 10;
temp2 *= 10;
// 每排完一位,位数减一
digits--;
}
}
} 输入数组:
453 677 888 525 275 322 123
运行结果:
123 275 322 453 525 677 888
以上为十大算法基本思想以及Java语言实现。