【pytorch学习笔记六】深度学习基础（线性回归、损失函数、梯度下降、欠拟合与过拟合，正则化）

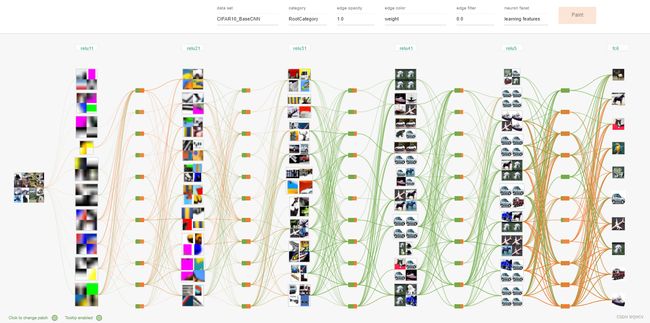
上面可视化深度学习网页网址：shixialiu.com/publications/cnnvis/demo/

深度学习是目前比较成功的表示学习的方法，是机器学习的一个分支。深度学习的基础理论学习可到B站上看吴恩达老师的深度学习课程，对应内容都有对应的练习题。下面介绍一些深度学习的常用概念：

1. 监督学习和无监督学习

监督学习、无监督学习、半监督学习、强化学习是我们日常接触到的常见的四个机器学习方法：

• 监督学习：通过已有的训练样本（即已知数据以及其对应的输出）去训练得到一个最优模型（这个模型属于某个函数的集合，最优则表示在某个评价准则下是最佳的），再利用这个模型将所有的输入映射为相应的输出。
• 无监督学习：它与监督学习的不同之处，在于我们事先没有任何训练样本，而需要直接对数据进行建模。
• 半监督学习 ：在训练阶段结合了大量未标记的数据和少量标签数据。与使用所有标签数据的模型相比，使用训练集的训练模型在训练时可以更为准确。
• 强化学习：我们设定一个回报函数（reward function），通过这个函数来确认否越来越接近目标，类似我们训练宠物，如果做对了就给他奖励，做错了就给予惩罚，最后来达到我们的训练目的。

本篇主要介绍监督学习，在训练和验证时输入的数据既包含输入x，又包含x对应的输出y，即学习数据已经事先给出了正确答案。

2. 线性回归

简单的说： 线性回归对于输入x与输出y有一个映射f，y=f(x),而f的形式为wx+b。其中a和b是两个可调的参数，我们训练的时候就是训练a，b这两个参数。下面是具体例子：

#如果提前没有安装seaborn可pip install seaborn 安装
import torch
from torch.nn import Linear, Module, MSELoss
from torch.optim import SGD
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns

x = np.linspace(0,20,500) #linspace(start,stop,num=50)
y = 5*x + 7
plt.plot(x,y)
plt.show()

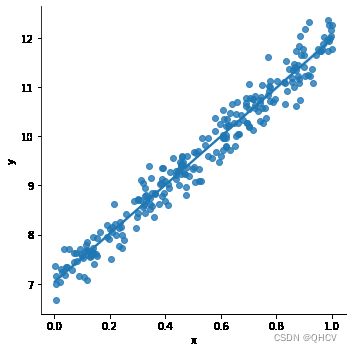
#随机生成一组点作为训练数据
x = np.random.rand(256)
noise = np.random.randn(256) / 4 #生成随机噪声
y = x * 5 + 7 + noise
df = pd.DataFrame() #新建一个DataFrame数据结构的变量
df['x'] = x
df['y'] = y
sns.lmplot(x='x', y='y', data=df)#绘制点图像

#定义一个model，输入长度是1，输出也是1
model=Linear(1, 1) #即y=wx+b
#均方损失函数：MSELoss ，输入x和目标y之间均方差
criterion = MSELoss()
#优化器我们选择最常见的优化方法 SGD(随机梯度下降)，就是每一次迭代计算 mini-batch 的梯度
#然后对参数进行更新，学习率 0.01
optim = SGD(model.parameters(), lr = 0.01)
#训练迭代次数
epochs = 3000
#准备训练集
x_train = x.reshape(-1, 1).astype('float32')#-1表示自动计算长度
y_train = y.reshape(-1, 1).astype('float32')
#开始训练
for i in range(epochs):
    # 整理输入和输出的数据，这里输入和输出一定要是torch的Tensor类型
    inputs = torch.from_numpy(x_train)#将NumPy数组转为tensor
    labels = torch.from_numpy(y_train)
    #使用模型进行预测
    outputs = model(inputs)
    #在训练过程中先调用 optimizer.zero_grad() 清空梯度，再调用 loss.backward() 反向传播，最后调用 optimizer.step()更新模型参数
    #梯度置0，否则会累加
    optim.zero_grad()
    # 计算损失
    loss = criterion(outputs, labels)
    # 反向传播
    loss.backward()
    # 使用优化器默认方法优化
    optim.step()#进行一次参数更新
    if (i%100==0):
        #每 100次打印一下损失函数，看看效果
        print('epoch {}, loss {:1.4f}'.format(i,loss.data.item())) 

epoch 0, loss 83.0969
epoch 100, loss 0.7176
epoch 200, loss 0.2271
epoch 300, loss 0.1910
epoch 400, loss 0.1648
epoch 500, loss 0.1444
epoch 600, loss 0.1286
epoch 700, loss 0.1162
epoch 800, loss 0.1066
epoch 900, loss 0.0992
epoch 1000, loss 0.0933
epoch 1100, loss 0.0888
epoch 1200, loss 0.0853
epoch 1300, loss 0.0825
epoch 1400, loss 0.0804
epoch 1500, loss 0.0788
epoch 1600, loss 0.0775
epoch 1700, loss 0.0765
epoch 1800, loss 0.0757
epoch 1900, loss 0.0751
epoch 2000, loss 0.0746
epoch 2100, loss 0.0742
epoch 2200, loss 0.0739
epoch 2300, loss 0.0737
epoch 2400, loss 0.0735
epoch 2500, loss 0.0734
epoch 2600, loss 0.0733
epoch 2700, loss 0.0732
epoch 2800, loss 0.0732
epoch 2900, loss 0.0731

[w,b] = model.parameters()
b.item() #item() -> number
print (w.item(),b.item()) #对应的y=wx+b中的参数

#y=wx+b中的参数W和b
4.909780502319336 7.049854278564453

predicted = model.forward(torch.from_numpy(x_train)).data.numpy()
plt.plot(x_train, y_train, 'go', label = 'data', alpha = 0.3)#g，o表示绿色，点
plt.plot(x_train, predicted, 'ro',label = 'predicted', alpha = 0.2)#alpha表示透明度
plt.legend()#作用是给图像加图例
plt.show()

​

以上就是线性回归的一个简单例子，深度学习的原理也与此类似。

3. 损失函数

损失函数（loss function） 也可称为代价函数 （Cost Function）或误差函数（Error Function）是用来估量模型的预测值(我们例子中的output)与真实值（例子中的y_train）的不一致程度，它是一个非负实值函数，损失函数越小，模型的鲁棒性就越好。 我们训练模型的过程，就是通过不断的迭代计算，使用梯度下降的优化算法，使得损失函数越来越小。损失函数越小就表示算法达到意义上的最优，只是训练集的结果之间的差异比较小，但是还没有在算法的真正预测上比较效果。常见的损失函数有：包括均方差损失 Mean Squared Loss、平均绝对误差损失 Mean Absolute Error Loss、Huber Loss、分位数损失 Quantile Loss、交叉熵损失函数 Cross Entropy Loss、Hinge 损失 Hinge Loss。在分类任务重多使用交叉熵损失函数。

具体损失函数介绍可看这篇文章：

【常见的损失函数总结】_菜菜雪丫头的博客-CSDN博客_损失函数总结

4.梯度下降

梯度下降是一个使损失函数越来越小的优化算法，在无求解机器学习算法的模型参数，即约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一。所以梯度下降是我们目前所说的机器学习的核心，了解了它的含义，也就了解了机器学习算法的含义。

4.1梯度

在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。 例如函数f(x,y), 分别对x，y求偏导数，求得的梯度向量就是(∂f/∂x, ∂f/∂y)T，简称grad f(x,y)或者▽f(x,y)。几何上讲，梯度就是函数变化增加最快的地方，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向梯度减少最快，也就是更加容易找到函数的最小值。

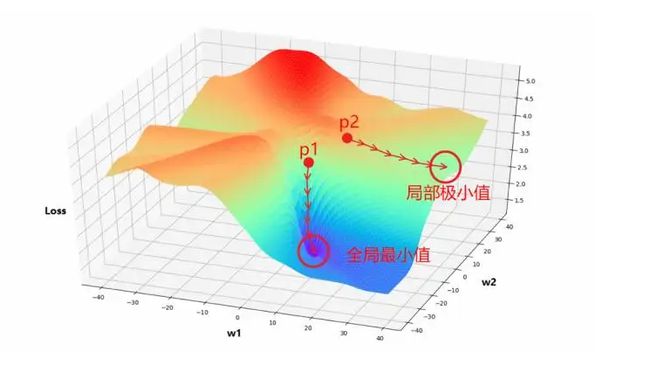
梯度下降法直观解释

梯度下降法就好比下山，我们并不知道下山的路，于是决定走一步算一步，每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。

这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处（局部最优解）。

这个问题在以前的机器学习中可能会遇到，因为机器学习中的特征比较少，所以导致很可能陷入到一个局部最优解中出不来，但是到了深度学习，动辄百万甚至上亿的特征，出现这种情况的概率几乎为0，所以我们可以不用考虑这个问题。

4.2 Mini-batch的梯度下降法

对整个训练集进行梯度下降法的时候，我们必须处理整个训练数据集，然后才能进行一步梯度下降，即每一步梯度下降法需要对整个训练集进行一次处理，如果训练数据集很大的时候处理速度会很慢，而且也不可能一次的载入到内存或者显存中，所以我们会把大数据集分成小数据集，一部分一部分的训练，这个训练子集即称为Mini-batch。 在PyTorch中就是使用这种方法进行的训练，可以看看上一章中关于dataloader的介绍里面的batch_size就是我们一个Mini-batch的大小。

对于普通的梯度下降法，一个epoch（所有训练的数据都输入模型中跑一次）只能进行一次梯度下降；而对于Mini-batch梯度下降法，一个epoch可以进行Mini-batch的个数次梯度下降，即每一小批的数据输入模型训练后就对训练的参数进行梯度下降更新一次。

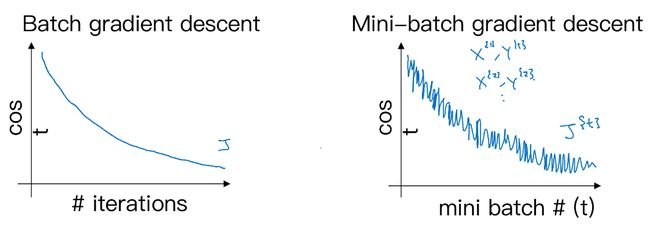
• 左图是 batch 梯度下降，横轴为迭代次数（epoch），纵轴为损失函数值。
• 右图是 mini-batch 梯度下降，横轴为用于更新权重的 mini-batch 数，纵轴为损失函数值，损失值整体趋势是下降的。

4.3 常见梯度下降算法

torch.optim.SGD

随机梯度下降算法，带有动量（momentum）的算法作为一个可选参数可以进行设置，样例如下：

#lr参数为学习率，对于SGD来说一般选择0.1 0.01.0.001
#如果设置了momentum，就是带有动量的SGD，可以不设置
optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9)#model.parameters()需要优化的模型参数

torch.optim.RMSprop

除了以上的带有动量Momentum梯度下降法外，RMSprop（root mean square prop）也是一种可以加快梯度下降的算法，利用RMSprop算法，可以减小某些维度梯度更新波动较大的情况，使其梯度下降的速度变得更快

optimizer = torch.optim.RMSprop(model.parameters(), lr=0.01, alpha=0.99)

torch.optim.Adam

Adam 优化算法的基本思想就是将 Momentum 和 RMSprop 结合起来形成的一种适用于不同深度学习结构的优化算法

# 这里的lr，betas，还有eps都是用默认值即可，所以Adam是一个使用起来最简单的优化方法
optimizer = torch.optim.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.999), eps=1e-08)

• params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
• lr – 学习率（默认：1e-3）
• betas– 用于计算梯度以及梯度平方的运行平均值的系数（默认：0.9，0.999）
• eps – 为了增加数值计算的稳定性而加到分母里的项加在分母上防止除0（默认：1e-8）
• weight_decay– 权重衰减（L2惩罚）（默认: 0）

详细可阅读：pytorch优化器详解：Adam_拿铁大侠的博客-CSDN博客_adam pytorch

5.欠拟合与过拟合（高偏差/高方差）

• 偏差度量了学习算法的期望预测与真实结果的偏离程序，即刻画了学习算法本身的拟合能力
• 方差度量了同样大小的训练集的变动所导致的学习性能的变化，即模型的泛化能力

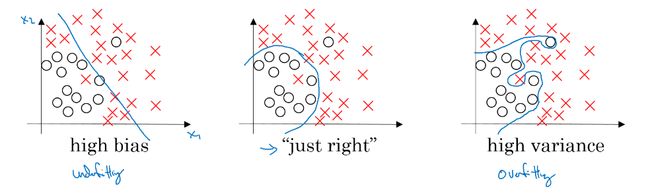
• 高偏差（high bias）的情况，一般称为欠拟合（underfitting），即我们的模型并没有很好的去适配现有的数据，拟合度不够。（可以理解为自己都没学好）
• 高方差（high variance）的情况一般称作过拟合（overfitting），即模型对于训练数据拟合度太高了，失去了泛化的能力。（自己学好了，但是教别人的时候只会自己学了的，没学到一样的就不会了，没有主观能动性）

解决方法

• 欠拟合： 增加网络结构，如增加隐藏层数目； 训练更长时间；寻找合适的网络架构，使用更大的网络结构；
• 过拟合 ： 使用更多的数据； -正则化（ regularization）； 寻找合适的网络结构；

6. 正则化

正则化来解决High variance 的问题，正则化是在 Cost function 中加入一项正则化项，惩罚模型的复杂度。如果正则化参数变得很大，参数W很小，z 也会相对变小，此时忽略b的影响，z会相对变小，实际上，z的取值范围很小，这个激活函数，也就是曲线函数会相对呈线性，整个神经网络会计算离线性函数近的值，这个线性函数非常简单，并不是一个极复杂的高度非线性函数，不会发生过拟合。

其数学表达形式为：
$$J(w;X,y)=J(w;X,y)+\alpha \Omega (w)$$
式中 X 、 y为训练样本和相应标签， w 为权重系数向量； J() 为目标函数， Ω(w) 即为惩罚项，可理解为模型“规模”的某种度量；参数α 控制控制正则化强弱。不同的 Ω 函数对权重 w 的最优解有不同的偏好，因而会产生不同的正则化效果。最常用的 Ω 函数有两种，即 l1 范数和 l2 范数，相应称之为 l1 正则化和 l2 正则化。此时有：
$$l1:\Omega (w)=||w|{|}_1=\sum _i|w_i|$$

$$l2:\Omega (w)=||w|{|}_2^2=\sum _i{w}_i^2$$

利用损失函数来求得模型 y(x) 和 真实数据 y 的误差, 而 L1 ，L2 就只是在这个误差公式后面多加了一个东西, 让误差不仅仅取决于拟合数据拟合的好坏, 而且取决于像刚刚其它大小。如果是每个参数的平方, 那么称它为 L2正则化, 如果是每个参数的绝对值, 称为 L1 正则化。

参考资料：

• https://zhuanlan.zhihu.com/p/29360425
• https://handbook.pytorch.wiki/chapter2/2.2-deep-learning-basic-mathematics.html

欢迎关注个人公众号【智能建造小硕】（分享计算机编程、人工智能、智能建造、日常学习和科研经验等，欢迎大家关注交流。）