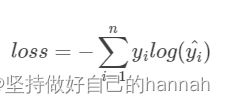机器学习/算法面试笔记1——损失函数、梯度下降、优化算法、过拟合和欠拟合、正则化与稀疏性、归一化、激活函数
正值秋招,参考网络资源整理了一些面试笔记,第一篇包括以下7部分。
1、损失函数
2、梯度下降
3、优化算法
4、过拟合和欠拟合
5、正则化与稀疏性
6、归一化
7、激活函数
损失函数
损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别,结构风险损失函数是指经验风险损失函数加上正则项。
常见的损失函数以及其优缺点如下:
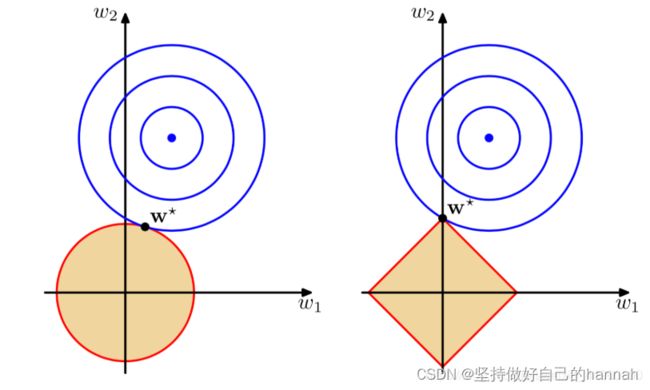
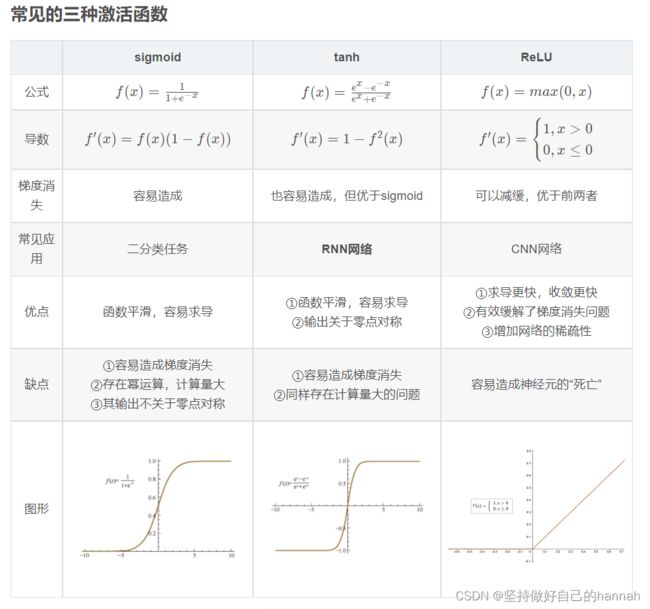
1、0-1损失函数(zero-one loss)
0-1损失是指预测值和目标值不相等为1, 否则为0:
特点:
(1)0-1损失函数是一个非凸函数,不太适用。
(2)感知机就是用的这种损失函数。但是相等这个条件太过严格,因此可以放宽条件,即满足 |Y−f(x)| 2、绝对值损失函数MAE 绝对值损失函数是计算预测值与目标值的差的绝对值:L(Y,f(x))=|Y−f(x)| 3、平方损失函数MSE 平方损失函数标准形式如下:L(Y|f(X))=∑N(Y−f(X))2 特点:经常应用于回归问题 MAE与MSE比较: MSE 通常比 MAE 可以更快地收敛。当使用梯度下降算法时,MSE 损失的梯度为 −yi^ ,而 MAE 损失的梯度为 ±1 ,即 MSE 的梯度的 scale 会随误差大小变化,而 MAE 的梯度的 scale 则一直保持为 1,即便在绝对误差 |yi−yi^| 很小的时候 MAE 的梯度 scale 也同样为 1,这实际上是非常不利于模型的训练的。当然你可以通过在训练过程中动态调整学习率缓解这个问题,但是总的来说,损失函数梯度之间的差异导致了 MSE 在大部分时候比 MAE 收敛地更快。这个也是 MSE 更为流行的原因。 但MAE 对于 outlier 更加 robust,即更加不易受到 outlier 影响。当误差非常大的时候,MSE 损失会远远大于 MAE 损失。因此当数据中出现一个误差非常大的 outlier 时,MSE 会产生一个非常大的损失,对模型的训练会产生较大的影响。 4、交叉熵损失函数 (Cross-entropy loss function) 交叉熵损失函数的标准形式如下: 特点: (1)本质上也是一种对数似然函数,可用于二分类和多分类任务中。输入数据是softmax或者sigmoid函数的输出。(对数损失函数和交叉熵损失函数应该是等价的。) (2)当使用sigmoid作为激活函数的时候,常用交叉熵损失函数而不用均方误差损失函数,因为它可以完美解决平方损失函数权重更新过慢的问题,具有“误差大的时候,权重更新快;误差小的时候,权重更新慢”的良好性质。 相关高频问题: (1)交叉熵函数与最大似然函数的联系和区别? 区别:交叉熵函数使用来描述模型预测值和真实值的差距大小,越大代表越不相近;似然函数的本质就是衡量在某个参数下,整体的估计和真实的情况一样的概率,越大代表越相近。 联系:交叉熵函数可以由最大似然函数在伯努利分布的条件下推导出来,或者说最小化交叉熵函数的本质就是对数似然函数的最大化。 (2)在用sigmoid作为激活函数的时候,为什么要用交叉熵损失函数,而不用均方误差损失函数? 分析一下两个误差函数的参数更新过程就会发现原因了。 因为sigmoid的性质,导致 σ′(x) 在 z 取大部分值时会很小(如下图标出来的两端,几乎接近于平坦),这样会使得 η(a−y)σ′(z) 很小,导致参数 w 和 b 更新非常慢。 交叉熵损失函数在参数更新公式中没有 σ′(x) 这一项,权重的更新受 (a−y) 影响,受到误差的影响,所以当误差大的时候,权重更新快;当误差小的时候,权重更新慢。这是一个很好的性质。 均方差损失假设了误差服从高斯分布,在分类任务下这个假设没办法被满足,因此效果会很差。 为什么是交叉熵损失呢?有两个角度可以解释这个事情,一个角度从最大似然的角度,也就是我们上面的推导;另一个角度是可以用信息论来解释交叉熵损失 5、合页损失函数Hinge Hinge损失函数标准形式如下:L(y,f(x))=max(0,1−yf(x)) 可以看到当 y 为正类时,模型输出负值会有较大的惩罚,当模型输出为正值且在 (0,1) 区间时还会有一个较小的惩罚。即合页损失不仅惩罚预测错的,并且对于预测对了但是置信度不高的也会给一个惩罚,只有置信度高的才会有零损失。使用合页损失直觉上理解是要找到一个决策边界,使得所有数据点被这个边界正确地、高置信地被分类。 特点: (1)hinge损失函数表示如果被分类正确,损失为0,否则损失就为 1−yf(x) 。SVM就是使用这个损失函数。 (2)一般的 f(x) 是预测值,在-1到1之间,y 是目标值(-1或1)。其含义是,f(x) 的值在-1和+1之间就可以了,并不鼓励 |f(x)|>1 ,即并不鼓励分类器过度自信,让某个正确分类的样本距离分割线超过1并不会有任何奖励,从而使分类器可以更专注于整体的误差。 (3) 健壮性相对较高,对异常点、噪声不敏感,但它没太好的概率解释。 6、log对数损失函数 log对数损失函数的标准形式如下:L(Y,P(Y|X))=−logP(Y|X) 特点: (1) log对数损失函数能非常好的表征概率分布,在很多场景尤其是多分类,如果需要知道结果属于每个类别的置信度,那它非常适合。 (2)健壮性不强,相比于hinge loss对噪声更敏感。 (3)逻辑回归的损失函数就是log对数损失函数。 7、指数损失函数(exponential loss) 指数损失函数的标准形式如下:L(Y|f(X))=exp[−yf(x)] 特点:对离群点、噪声非常敏感。经常用在AdaBoost算法中。 8、感知损失(perceptron loss)函数 感知损失函数的标准形式如下:L(y,f(x))=max(0,−f(x)) 特点:是Hinge损失函数的一个变种,Hinge loss对判定边界附近的点(正确端)惩罚力度很高。而perceptron loss只要样本的判定类别正确的话,它就满意,不管其判定边界的距离。它比Hinge loss简单,因为不是max-margin boundary,所以模型的泛化能力没 hinge loss强。 梯度下降 批量梯度下降法(Batch Gradient Descent,BGD)就好比正常下山,而随机梯度下降法就好比蒙着眼睛下山,数学上的表达式为。 批量梯度下降法在全部训练集上计算准确的梯度。为了获取准确的梯度,批量梯度下降法的每一步都把整个训练集载入进来进行计算,时间花费和内存开销都非常大,无法应用于大数据集、大模型的场景。 随机梯度下降法则采样单个样本来估计当前的梯度。随机梯度下降法则放弃了对梯度准确性的追求,每步仅仅随机采样一个(或少量)样本来估计当前梯度,计算速度快,内存开销小。但由于每步接受的信息量有限,随机梯度下降法对梯度的估计常常出现偏差,造成目标函数曲线收敛得很不稳定,伴有剧烈波动,有时甚至出现不收敛的情况。 批量梯度下降法稳定地逼近最低点,而随机梯度下降法的参数轨迹曲曲折折简直是“黄河十八弯"。 mini-batch梯度下降: 在每次更新时用b个样本,其实批量的梯度下降就是一种折中的方法,他用了一些小样本来近似全部的,其本质就是我1个指不定不太准,那我用个30个50个样本那比随机的要准不少了吧,而且批量的话还是非常可以反映样本的一个分布情况的。在深度学习中,这种方法用的是最多的,因为这个方法收敛也不会很慢,收敛的局部最优也是更多的可以接受! 在小批量梯度下降中,有三点需要注意的地方: 深度学习中最常用的优化方法就是随机梯度下降法,但其偶尔也会失效。 随机梯度下降和批量梯度下降都会陷入局部最优的陷阱。对随机梯度下降法来说,最可怕的时山谷和鞍点两种地形。在梯度近乎为零的区域,随机梯度下降法无法准确察觉出梯度的微小变化,结果就停滞下来。 优化方法 优化方法大致分为两类: 与随机梯度下降法(SDG)不同的是,它保存了历史的梯度,解决SDG方法在山谷震荡和鞍点停滞的问题。 用之前积累的动量来替代真正的梯度,每次迭代的梯度可以看做加速度。 加入动量因子可以减少偏移量。向下的力稳定不变,产生的动量不断累积,速度越来越快;左右的弹力总是在不停切换,动量累积的结果相互抵消,减弱了球的来回震荡。与SDG方法相比,动量方法的收敛速度更快,收敛曲线也更稳定。 常用的学习率调整方法包括学习率衰减、学习率预热、周期性学习率调整以及一些自适应调整学习率的方法,比如AdaGrad、RMSprop、AdaDelta。 惯性的力是基于历史的,我们还期待获得对周围环境的感知。希望更新频率低的参数可以拥有较大的更新步幅,而更新频率高的参数参数步幅可以减小。 AdaGrad方法采用“历史梯度平方和”来衡量不同参数的梯度的稀疏性,取值越小表明越稀疏。 AdaGrad方法采用所有历史梯度平方和作为分母,分母随时间单调递增,产生的自适应学习率随时间衰减的速度过于激进。 RMSProp算法不是像AdaGrad算法那样暴力直接的累加平方梯度,而是加了一个衰减系数来控制历史信息的获取多少。可以避免AdaGrad算法中学习率不断单调下降以至于过早衰减。 将惯性保持和环境感知这两个优点集于一身。一方面记录梯度的一阶矩,即过往梯度与当前梯度的平均,保持了惯性;另一方面记录梯度的二阶矩,体现了环境感知能力,为不同参数产生自适应的学习速率。一阶矩和二阶矩采用类似于滑动窗口内求平均的思想进行融合。 过拟合和欠拟合 过拟合的原因: 过拟合解决办法: 如果不是很容易,可以通过图像平移、旋转、缩放等,还可以使用迁移学习技术。 如决策树中降低树的高度、进行剪枝等。 如L2将权值大小引入到损失函数中 添加BN层 使用dropout(dropout在训练时会随机隐藏一些神经元,导致训练过程不会每次都更新) 在模型对训练数据集迭代收敛之前停止迭代 具体做法:在一个epoch结束时计算validation data的accuracy,当其不再提高就停止训练。 就是把多个模型集成在一起。如Bagging,首先对原始m个训练样本进行有放回随机抽样,构建N组m个样本的数据集,用N组数据集训练网络,得到N组参数,进行加权平均。 但要花费更多时间和空间 将数据切成S个互不相交大小相同的自己,用S-1子集的数据训练模型,余下的测试;将这一过程对可能的S中选择重复进行,选择S次当中平均测试误差最小的模型。 欠拟合的原因: 欠拟合的解决办法: 欠拟合会导致高 Bias ,过拟合会导致高 Variance,所以模型需要在 Bias 与 Variance 之间做出一个权衡。 正则化与稀疏项 为什么希望模型参数具有稀疏性? 相当于对模型进行了一次特征选择,只留下一些比较重要的特征,提高模型的泛化能力,降低过拟合的可能。 原理:在损失函数上加上某些限制,缩小解空间,从而减少求出过拟合解的可能性。 不同次方下的正则项(左:L2正则 右:L1正则) 二次正则项的优势,处处可导,方便计算。 L2正则化对于绝对值较大的权重予以很重的惩罚,对于绝对值很小的权重予以非常非常小的惩罚,当权重绝对值趋近于0时,基本不惩罚。这个性质与L2的平方项有关系,即越大的数,其平方越大,越小的数,比如小于1的数,其平方反而越小。 同时,他有另一个优势,在使用正规方程时,解析式中的逆始终存在的。 L2正则化只是使得模型的参数值趋近于0,而不是等于0,这样就无法丢掉模型里的任何一个特征,因此无法做到稀疏化。这时,L1的作用随之显现。L1正则化的作用是使得大部分模型参数的值等于0,这样一来,当模型训练好后,这些权值等于0的特征可以省去,从而达到稀疏化的目的,也节省了存储的空间。 L1在确实需要稀疏化模型的场景下,才能发挥很好的作用并且效果远胜于L2。在模型特征个数远大于训练样本数的情况下,如果我们事先知道模型的特征中只有少量相关特征(即参数值不为0),并且相关特征的个数少于训练样本数,那么L1的效果远好于L2。然而,需要注意的是,当相关特征数远大于训练样本数时,无论是L1还是L2,都无法取得很好的效果。 归一化 归一化的提出 机器学习领域,数据分布很重要。如果训练集和测试机分布很不相同,那可能训练好的模型在测试机上不奏效。 对神经网络来说,如果每层数据分布不一样,那么后一次网络要去学习适应迁移侧耳数据分布,加大了训练难度。 “Internal Covariate Shift”对于深度学习而言,会包含多个隐层结构,每一层隐层都有自己的输入,在训练过程中,隐层的输入分布经常发生变化。“Internal Covariate Shift”会导致模型的学习速率变慢,学习效果也可能会受到影响。 对于深层的神经网络而言,经过多层神经网络后,输出值往往会变大很多或者很小,如果激活函数是sigmoid的话,会导致梯度消失的情况。 基于以上两点(“Internal Covariate Shift”和梯度消失),则产生了归一化的需要。 BN特点: 强行将数据转为均值为0,方差为1的正态分布,使得数据分布一致,并且避免梯度消失。而梯度变大意味着学习收敛速度快,能够提高训练速度。 BN的好处: 输出分布向着激活函数的上下限偏移,带来梯度的降低(如sigmoid),通过归一化,数据在一个合适的分布空间,通过激活函数仍能有不错的梯度。梯度好了自然加速训练。 在训练中,BN的使用使得一个mini-batch中的所有样本都被关联在了一起,因此网络不会从某一个训练样本中生成确定的结果。意思就是同样一个样本的输出不再仅仅取决于样本本身,也取决于跟这个样本属于同一个mini-batch的其它样本。 问题: 当batch size越小,BN表现越不好,因为计算过程中得到的均值方差不能代表全局。 BatchNorm与LayerNorm Batch 顾名思义是对一个batch进行操作。假设我们有 10行 3列 的数据,即我们的batchsize = 10,每一行数据有三个特征,假设这三个特征是【身高、体重、年龄】。那么BN是针对每一列(特征)进行缩放,例如算出【身高】的均值与方差,再对身高这一列的10个数据进行缩放。体重和年龄同理。这是一种“列缩放”。 而layer方向相反,它针对的是每一行进行缩放。即只看一笔数据,算出这笔所有特征的均值与方差再缩放。这是一种“行缩放”。完全独立于batch size。 为什么要使用LN呢?因为NLP领域中,LN更为合适。 如果我们将一批文本组成一个batch,那么BN的操作方向是,对每句话的第一个词进行操作。但语言文本的复杂性是很高的,任何一个词都有可能放在初始位置,且词序可能并不影响我们对句子的理解。而BN是针对每个位置进行缩放,这不符合NLP的规律。 而LN则是针对一句话进行缩放的,且LN一般用在第三维度,如[batchsize, seq_len, dims]中的dims,一般为词向量的维度,或者是RNN的输出维度等等,这一维度各个特征的量纲应该相同。因此也不会遇到上面因为特征的量纲不同而导致的缩放问题。 小结: BN 和 LN 都可以比较好的抑制梯度消失和梯度爆炸的情况。BN不适合RNN、transformer等序列网络,不适合文本长度不定和batchsize较小的情况,适合于CV中的CNN等网络; 而LN适合用于NLP中的RNN、transformer等网络,因为sequence的长度可能是不一致的。 (1)经过BN的归一化再输入激活函数,得到的值大部分会落入非线性函数的线性区,导数远离导数饱和区,避免了梯度消失,这样来加速训练收敛过程。 (2)归一化技术就是让每一层的分布稳定下来,让后面的层能在前面层的基础上“安心学习”。BatchNorm就是通过对batch size这个维度归一化来让分布稳定下来(但是BN没有解决ISC问题)。LayerNorm则是通过对Hidden size这个维度归一。 激活函数 为什么使用激活函数? 不使用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合。使用激活函数,能够给神经元引入非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以利用到更多的非线性模型中。 总结:在神经网络中引入非线性因素,增加模型的拟合能力。 激活函数需要具备以下几点性质: 非线性;计算简单;可微;单调 (1)连续并可导(允许少数点上不可导)的非线性函数。可导的激活函数可以直接利用数值优化的方法来学习网络参数。 (2)激活函数及其导函数要尽可能的简单,有利于提高网络计算效率。 (3)激活函数的导函数的值域要在一个合适的区间内,不能太大也不能太小,否则会影响训练的效率和稳定性。 激活函数不会改变数据的维度,也就是输入和输出的维度是相同的。 1、相对于sigmoid函数,tanh激活函数关于零点对称的好处是什么? sigmoid函数输出始终为正,在反向传播求导时,权重更新效率会降低,导致模型收敛速度变慢。 此外,sigmoid输出均大于0,作为下层神经元的输入会导致下层输入不是0均值的,随着网络加深可能导致原始数据分布发生变化。 Sigmoid函数输出在[0 , 1]之间,适合二分类问题。 2、RNN中为什么用tanh而不用RELU激活? 因为RELU的导数智能为0或1,导数为1时RNN很容易产生梯度爆炸。因为RNN中,每个神经元在不同时刻共享一个参数(而CNN每一次都是独立的参数),如果W大于1,进行连乘,就会出现梯度爆炸问题。 3、ReLU函数在0处不可导,为什么在深度学习网络中还这么常用? 可以设置一个伪梯度,如定义其在0处的导数为0。 RELU的好处: 形式简洁; 可以解决sigmoid的梯度消失问题; RELU有单侧抑制,会使一部分神经元输出为0,造成了网络的稀疏性,缓和了过拟合问题; 计算速度快 RELU缺点: 导致神经元死亡,权重无法更新。 如果学习率没有设置好,更新权重输入是负值,那么这个含有RELU的神经节点就会死亡,不再被激活。 4、如何使用RELU神经元“死亡”问题(当有大梯度流入某个神经元后,导致神经元对其他梯度不敏感) 使用Leaky RELU等激活函数;Leaky RELU=max(ax, x),a是一个极小的系数,给负数区域一个很小的输出,不让其置0,从某种程度上避免了使部分神经元死掉的问题。 设置较小的学习率进行训练 使用momentun优化算法动态调整学习率 5、Gelu激活函数 gelu(gaussian error linear units)就是我们常说的高斯误差线性单元,它是一种高性能的神经网络激活函数,因为gelu的非线性变化是一种符合预期的随机正则变换方式。 对于是分类任务的输出层,二分类的输出层的激活函数常选择sigmoid函数;多分类就是softmax。对于隐藏层的激活函数通常会选择使用ReLU函数,保证学习效率。 第二期笔记打算整理一些典型的机器学习算法,下周(或者下下周)见~