贝叶斯实验报告（三）

一、实验目的

学会使用pymc3构建模型，解决短信数据推断行为以及A-B测试问题。

二、实验内容及步骤（包括问题，代码，结果和结论）

2.1 短信数据推断行为

题目:

代码：

数据读入和展示：

import pymc3 as pm
import matplotlib.pyplot as plt
import numpy as np

plt.figure(figsize=(12.5, 3.5))
count_data = np.loadtxt("./txtdata.csv")
n_count_data = len(count_data)
plt.bar(np.arange(n_count_data), count_data, color='#348ABD')
plt.xlabel("Time (days)")
plt.ylabel("Text messages received")
plt.title("Did the user's texting habits change over time?")
plt.xlim(0, n_count_data)

构建模型：

with pm.Model() as model:
    alpha = 1.0 / count_data.mean()
    lambda_1 = pm.Exponential("lambda_1", alpha)
    lambda_2 = pm.Exponential("lambda_2", alpha)
    
    tau = pm.DiscreteUniform("tau", lower=0, upper=n_count_data)
    
    with model:
        idx = np.arange(n_count_data)
        lambda_ = pm.math.switch(tau >= idx, lambda_1, lambda_2)
        #print(tau>=idx)
    with model:
        observation = pm.Poisson("obs", lambda_, observed=count_data)
    with model:
        step = pm.Metropolis()
        trace = pm.sample(10000, tune=5000, step=step)
    
        lambda_1_samples = trace['lambda_1']
        lambda_2_samples = trace['lambda_2']
        tau_samples = trace['tau']
        print(lambda_1_samples)
        print(lambda_2_samples)

结果展示：

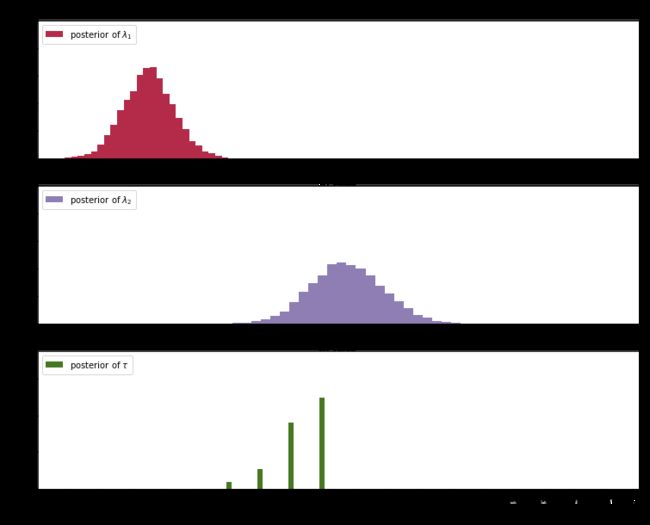
绘制三个参数的后验直方图:

plt.figure(figsize=(12.5, 10))

ax = plt.subplot(311)

ax.set_autoscaley_on(False)
plt.hist(lambda_1_samples, histtype='stepfilled', bins=30, alpha=0.85,
        label='posterior of $\lambda_1$', color='#A60628', density=True)

plt.legend(loc='upper left')
plt.title(r"""Posterior distributions of the varibles $\lambda_1,\;\lambda_2,\;\tau$""")
plt.xlim([15, 30])
plt.xlabel("$\lambda_1$ value")

ax = plt.subplot(312)
ax.set_autoscaley_on(False)
plt.hist(lambda_2_samples, histtype='stepfilled', bins=30, alpha=0.85,
        label='posterior of $\lambda_2$', color="#7A68A6", density=True)
plt.legend(loc='upper left')
plt.xlim([15,30])
plt.xlabel("$\lambda_2$ value")

plt.subplot(313)
w = 1.0 / tau_samples.shape[0] * np.ones_like(tau_samples)
plt.hist(tau_samples, bins=n_count_data, alpha=1, label=r"posterior of $\tau$",
        color='#467821', weights=w, rwidth=2)
plt.xticks(np.arange(n_count_data))

plt.legend(loc='upper left')
plt.ylim([0, .75])
plt.xlim([35, len(count_data) - 20])
plt.xlabel(r"$\tau$ (in days)")
plt.ylabel("probability")
plt.show()

结论：

1.λ1大概为18，λ2大概为23，这两个λ的后验分布有显著差异，表明用户接收短信的行为确实发生了变化。

2.λ的后验分布并不像指数分布，事实上后验分布并不是我们从原始模型中可以辨别的任何分布，用计算机可以很好展示出来。

3.τ是离散变量，后验分布有所不同，50%把握说明用户在44天行为改变。

结果展示：

绘制拟合的结果：

plt.figure(figsize=(12.5, 5))

N = tau_samples.shape[0]
excepted_texts_per_day = np.zeros(n_count_data)
for day in range(0, n_count_data):
    ix = day < tau_samples
    excepted_texts_per_day[day] = (lambda_1_samples[ix].sum()
                                  +lambda_2_samples[~ix].sum()) / N

plt.plot(range(n_count_data), excepted_texts_per_day, lw=4, color='#E24A33',
        label="expected number of text-messages received")
plt.xlim(0, n_count_data)
plt.xlabel("Day")
plt.ylabel("Excepted number of text-messages received")
plt.ylim(0, 60)
plt.bar(np.arange(len(count_data)), count_data, color="#348ABD", alpha=0.65,
       label='observed texts per day')
plt.legend(loc="upper left")

结论：

观察上图中的结果发现，分析的结果很符合之前的估计，用户的行为确 实发生了改变，而且变化是很突然的，所以可以推测情况产生的原因可能是：短信资费降低，或者逢年过节期间，或者天气提醒短信订阅等等。

2.2 短信数据推断行为(拓展)

题目：

代码：

构建模型：

with pm.Model() as model:
    alpha = 1.0 / count_data.mean()
    lambda_1 = pm.Exponential("lambda_1", alpha)
    lambda_2 = pm.Exponential("lambda_2", alpha)
    lambda_3 = pm.Exponential("lambda_3", alpha)
    
    tau_1 = pm.DiscreteUniform("tau_1", lower=0, upper=n_count_data)
    tau_2 = pm.DiscreteUniform("tau_2", lower=0, upper=n_count_data)
    with model:
        idx = np.arange(n_count_data)
        #pm.math.switch(tau_2>=idx, lambda_2, lambda_3)
        lambda_ = pm.math.switch(tau_1>=idx, lambda_1, pm.math.switch(tau_2>=idx, lambda_2, lambda_3))
        #print(lambda_)
    with model:
        observation = pm.Poisson("obs", lambda_, observed=count_data)
    with model:
        step = pm.Metropolis()
        trace = pm.sample(10000, tune=5000, step=step)
    
        lambda_1_samples = trace['lambda_1']
        lambda_2_samples = trace['lambda_2']
        lambda_3_samples = trace['lambda_3']
        tau_1_samples = trace['tau_1']
        tau_2_samples = trace['tau_2']
        print(tau_1_samples)
        print(lambda_1_samples.sum())
        print(lambda_2_samples.sum())
        print(lambda_3_samples.sum())

结果展示：

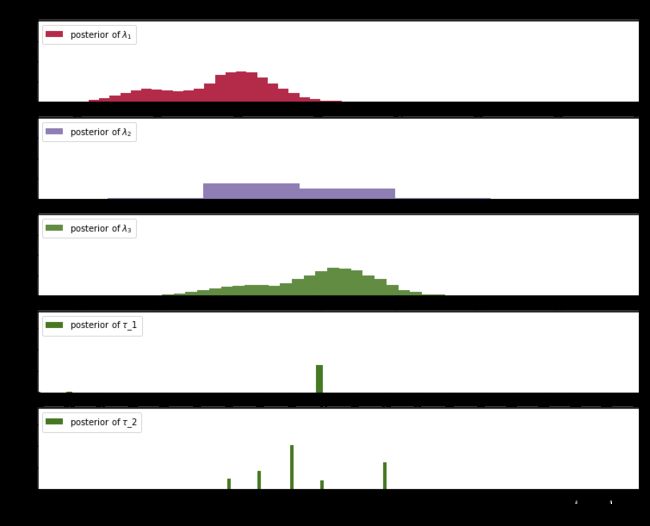
绘制五个参数的后验直方图:

plt.figure(figsize=(12.5, 10))

ax = plt.subplot(511)
ax.set_autoscaley_on(False)
plt.hist(lambda_1_samples, histtype='stepfilled', bins=30, alpha=0.85,
        label='posterior of $\lambda_1$', color='#A60628', density=True)

plt.legend(loc='upper left')
plt.title(r"""Posterior distributions of the varibles $\lambda_1,\;\lambda_2,\;\tau$""")
plt.xlim([15, 30])
plt.xlabel("$\lambda_1$ value")

ax = plt.subplot(512)
ax.set_autoscaley_on(False)
plt.hist(lambda_2_samples, histtype='stepfilled', bins=30, alpha=0.85,
        label='posterior of $\lambda_2$', color="#7A68A6", density=True)
plt.legend(loc='upper left')
plt.xlim([5,20])
plt.xlabel("$\lambda_2$ value")

ax = plt.subplot(513)
ax.set_autoscaley_on(False)
plt.hist(lambda_3_samples, histtype='stepfilled', bins=30, alpha=0.85,
        label='posterior of $\lambda_3$', color='#467821', density=True)

plt.legend(loc='upper left')
plt.xlim([15, 30])
plt.xlabel("$\lambda_3$ value")

plt.subplot(514)
w = 1.0 / tau_1_samples.shape[0] * np.ones_like(tau_1_samples)
plt.hist(tau_1_samples, bins=n_count_data, alpha=1, label=r"posterior of $\tau$_1",
        color='#467821', weights=w, rwidth=2)
plt.xticks(np.arange(n_count_data))
plt.legend(loc='upper left')
plt.ylim([0, .75])
plt.xlim([35, len(count_data) - 20])
plt.xlabel(r"$\tau$_1 (in days)")
plt.ylabel("probability")

plt.subplot(515)
w = 1.0 / tau_2_samples.shape[0] * np.ones_like(tau_2_samples)
plt.hist(tau_2_samples, bins=n_count_data, alpha=1, label=r"posterior of $\tau$_2",
        color='#467821', weights=w, rwidth=2)
plt.xticks(np.arange(n_count_data))
plt.legend(loc='upper left')
plt.ylim([0, .75])
plt.xlim([35, len(count_data) - 20])
plt.xlabel(r"$\tau$_2 (in days)")
plt.ylabel("probability")

plt.show()

结论：

1.λ1大概为20，λ2大概为10，λ3大概为23,这三个λ的后验分布有显著差异，表明用户接收短信的行为确实发生了变化。

2.λ的后验分布并不像指数分布，事实上后验分布并不是我们从原始模型中可以辨别的任何分布，用计算机可以很好展示出来。

3.τ是离散变量，后验分布有所不同，40%把握说明用户在43天行为改变。

结果展示：

绘制拟合的结果：

plt.figure(figsize=(12.5, 5))

N = tau_1_samples.shape[0]
excepted_texts_per_day = np.zeros(n_count_data)
for day in range(0, n_count_data):
    ix = day<tau_1_samples
    iy = day>tau_2_samples
    iz = day>tau_1_samples
    if ix.sum()/len(ix) == 1:
        excepted_texts_per_day[day] = (lambda_1_samples.sum())/N
    elif iy.sum()/len(iy) == 1:
        excepted_texts_per_day[day] = (lambda_3_samples.sum())/N
    else:
        excepted_texts_per_day[day] = (lambda_2_samples.sum())/N
    
plt.plot(range(n_count_data), excepted_texts_per_day, lw=4, color='#E24A33',
        label="expected number of text-messages received")
plt.xlim(0, n_count_data)
plt.xlabel("Day")
plt.ylabel("Excepted number of text-messages received")
plt.ylim(0, 60)
plt.bar(np.arange(len(count_data)), count_data, color="#348ABD", alpha=0.65,
       label='observed texts per day')
plt.legend(loc="upper left")

结论：

观察上图中的结果发现，分析的结果很符合之前的估计，用户的行为确 实发生了改变，而且变化是很突然的，所以可以推测情况产生的原因可能是：短信资费降低，或者逢年过节期间，或者天气提醒短信订阅等等。

2.3 A-B测试

题目：

2.3.1 方法一

先验分布取Beta分布是个好主意（转化率在0到1之间，刚好和Beta分布 值域一致）。而当样本是二项分布时，参数的共轭先验分布族是Beta分布，所以不需要进行MCMC采样。

代码：

导入需要的库：

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pymc3 as pm
from scipy.stats import beta
from IPython.core.pylabtools import figsize

导入需要的数据：

visitors_to_A=1300
visitors_to_B=1300
conversions_from_A=120
conversions_from_B=125
alpha_prior=1
beta_prior=1

得到后验分布，进行采样:

posterior_A=beta(alpha_prior+conversions_from_A,
                beta_prior+visitors_to_A-conversions_from_A)
posterior_B=beta(alpha_prior+conversions_from_B,
                beta_prior+visitors_to_B-conversions_from_B)
samples=2000
samples_posterior_A=posterior_A.rvs(samples)
samples_posterior_B=posterior_B.rvs(samples)

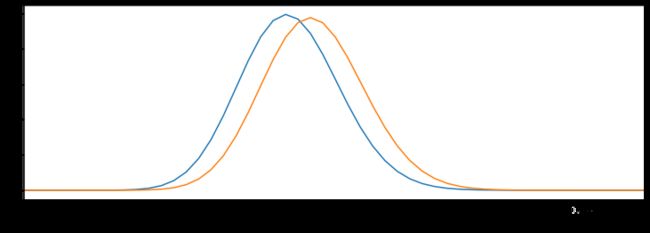
画出后验直方图，估计$p_A$，$p_B$:

plt.figure(figsize=(12.5,4))
plt.rcParams['savefig.dpi']=300
plt.rcParams['figure.dpi']=300
x=np.linspace(0,1,500)
plt.plot(x,posterior_A.pdf(x),label='posterior of A')
plt.plot(x,posterior_B.pdf(x),label='posterior of B')
plt.xlim(0.05,0.15)
plt.xlabel('value')

2.3.2 方法二

利用MCMC方法进行采样。

代码：

导入需要的库：

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pymc3 as pm
from scipy.stats import beta
from IPython.core.pylabtools import figsize

产生模拟数据：

p_true=0.05
N=1500
occurrences=stats.bernoulli.rvs(p_true,size=N)
print("What is the observed frequency in Group A?%.4f"%np.mean(occurrences))
print("Does this equal the true frequency?%s"%(np.mean(occurrences)==p_true))

构建模型，导入需要的数据:

with pm.Model() as model:
    p=pm.Uniform('p',lower=0,upper=1)
    obs=pm.Bernoulli('obs',p=p,observed=occurrences)
    step=pm.Metropolis()
    trace=pm.sample(12000,tune=1200,step=step,cores=2)
    burned_trace=trace[1000:]
    pm.traceplot(trace)

检查采样结果 :

 pm.traceplot(trace)

画出后验分布图:

plt.figure(figsize=(12.5,4))
plt.title("Posterior distribution of $p_A$,the true effectiveness of site A")
plt.vlines(p_true,0,90,linestyles="--",label='true $p_A$(unknown)')
plt.hist(burned_trace['p'],bins=25,histtype='stepfilled',density=True)
plt.legend()
plt.show()

2.4 A-B测试(拓展)

题目：

代码：

选取均匀分布为先验分布。

导入需要的库：

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pymc3 as pm
from scipy.stats import beta
from IPython.core.pylabtools import figsize

产生模拟数据:

true_p_A=0.05
true_p_B=0.04
N_A=1500
N_B=750
observations_A=stats.bernoulli.rvs(true_p_A,size=N_A)
observations_B=stats.bernoulli.rvs(true_p_B,size=N_B)

构建模型，导入需要的数据:

with pm.Model() as model:
    p_A=pm.Uniform('p_A',0,1)
    p_B=pm.Uniform('p_B',0,1)
    delta=pm.Deterministic('delta',p_A-p_B)
    obs_A=pm.Bernoulli('obs_A',p_A,observed=observations_A)    
    obs_B=pm.Bernoulli('obs_B',p_B,observed=observations_B)
    step=pm.Metropolis()
    trace=pm.sample(20000,step=step,cores=1)
    burned_trace=trace[1000:]

结果展示：

p_A_samples=burned_trace["p_A"]
p_B_samples=burned_trace["p_B"]
delta_samples=burned_trace["delta"]
plt.figure(figsize=(12.5,4))
plt.figure(1)
ax=plt.subplot(311)
plt.xlim(0,.1)
plt.hist(p_A_samples,histtype='stepfilled',bins=25,alpha=0.85,
        label="posterior of $p_A$",color="#A60628",density=True)
plt.vlines(true_p_A,0,80,linestyle="--",label="true $p_A$(unknown)")
plt.legend(loc="upper right")
plt.title("Poserior distributions of $p_A$,$_B$,and delta unknowns")

ax=plt.subplot(312)
plt.xlim(0,.1)
plt.hist(p_B_samples,histtype='stepfilled',bins=25,alpha=0.85,
        label="posterior of $p_B$",color="#467821",density=True)
plt.vlines(true_p_B,0,80,linestyle="--",label="true $p_B$(unknown)")
plt.legend(loc="upper right")
ax=plt.subplot(313)
plt.hist(delta_samples,histtype='stepfilled',bins=30,alpha=0.85,
        label="posterior of delta",color="#7A68A6",density=True)
plt.vlines(true_p_A-true_p_B,0,60,linestyle="--",label="true delta(unknown)")
plt.vlines(0,0,60,color="black",alpha=0.2)
plt.legend(loc="upper right")

plt.figure(2)
plt.xlim(0,.1)
plt.hist(p_A_samples,histtype='stepfilled',bins=30,alpha=0.80,
        label="posterior of $p_A$",color='#A60628',density=True)
plt.hist(p_B_samples,histtype='stepfilled',bins=30,alpha=0.80,
        label="posterior of $p_B$",color='#467821',density=True)
plt.legend(loc='upper right')
plt.xlabel("Value")
plt.ylabel("Density")
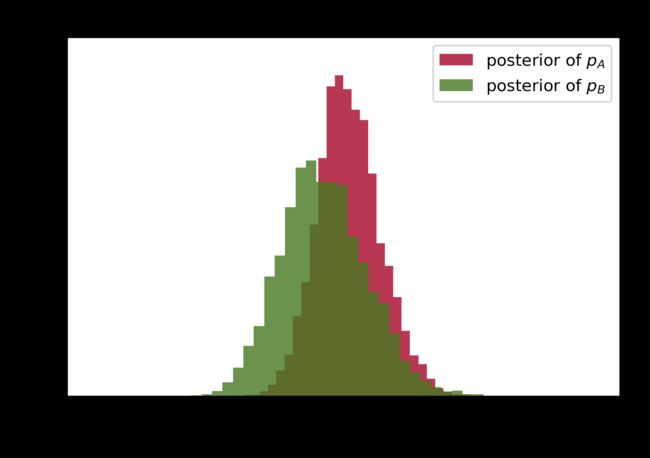
plt.title('Posterior distribution of $p_A$ and $p_B$')
plt.ylim(0,80)
plt.show()

比较$p_A$,$p_B$大小

print("Probability site A is WRSE than site B:%.3f"%np.mean(delta_samples<0))
print("Probability site A is BETTER than site B:%.3f"%np.mean(delta_samples>0))

三、实验体会

通过本次实验，我对pymc3的使用更加熟悉，同时也对贝叶斯统计推断理解得更透彻。在实验过程中遇到困难要及时和老师同学们交流，以便实验的顺利进行，希望后续实验能对贝叶斯统计推断掌握得更好。