【人工智能】十五数码问题：A*算法

应用A*算法解决十五数码问题（N数码），算法介绍：问题求解：启发式搜索算法，参考：Python实现A算法解决N数码问题 / A启发式搜索算法详解。完整代码：Python解决十五数码问题（程序、报告）

1.问题描述

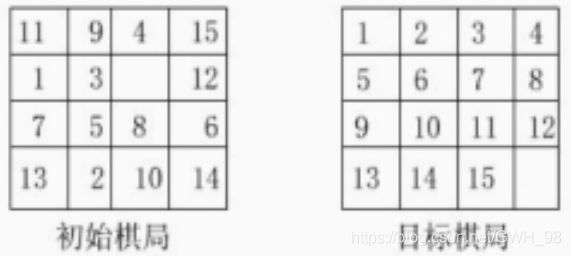
在4×4的棋盘上，摆有十五个棋子，每个棋子上标有1至15的某一数字。棋盘中留有一个空格，空格用0来表示。空格周围的棋子可以移到空格中（即空格可以上下左右移动）。要求解的问题是：给出一种初始布局：[11, 9, 4, 15, 1, 3, 0, 12, 7, 5, 8, 6, 13, 2, 10, 14]和目标布局：[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0]，找到一种最少步骤的移动方法，实现从初始布局到目标布局的转变。

2.启发函数设计

1）估价函数①：f(n)=d(n)+h(n)
d(n)为n的深度；
h(n)为不在位的棋子数。
这样h(n)≤h*(n)，是满足A* 算法的限制条件，所有一定能找到最优解，但是这样设计估价函数并不是最优的。

# Calculate hn1
def cal_hn1(c_state, g_state):
    hn = 0
    N = len(c_state)
    for i in range(N):
        for j in range(N):
            if c_state[i][j] == g_state[i][j]:
                continue
            hn += 1
    return hn

2）估价函数②：f(n)=d(n)+h(n)
d(n)为n的深度；
h(n)为不在位的棋子与其目标位置的距离的绝对值之和。
这样h(n)≤h*(n)，也是满足A* 算法的限制条件；1）中的h(n)是不在位的棋子数，不够贴切，错误选用节点加以扩展，而这里的h(n)是更接近于h*(n)的，其值是节点n与目标状态节点相比较，每个错位棋子在假设不受阻拦的情况下，移动到目标状态相应位置所需走步的总和。h(n)不仅考虑了错位因素，还考虑了错位的距离（移动次数），也就是启发性信息更多了。
每一步代价D为1。
曼哈顿距离:h(n) = D * (abs ( n.x – goal.x ) + abs ( n.y – goal.y ) )

# Calculate hn2
def cal_hn2(c_state, g_state):
    hn = 0
    N = len(c_state)
    for i in range(N):
        for j in range(N):
            if c_state[i][j] == g_state[i][j]:
                continue
            if c_state[i][j] == 0:
                x = N - 1
                y = N - 1
            else:
                x = (c_state[i][j] - 1) // N
                y = (c_state[i][j] - 1) % N
            hn += (abs(x - i) + abs(y - j))
    return hn

3.堆排序：O (nlgn)

在实际程序设计中，因为需要对大量的节点进行排序，如果排序算法时间复杂度高，会严重影响算法的运行速度，这里通过堆排序的方法，先将OPEN表转换为堆结构，减小排序算法的时间复杂度。
1）堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。堆排序就是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。
2）堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了
3）Python中的堆排序：Python的标准库中提供了堆排序模块heapq。对于储存节点的OPEN表可以通过：heap.heapify(OPEN)直接转换为堆结构，heapq.heappush(state)将子节点push到堆中，heapq.heappop(OPEN)可以直接将子节点中估值最小的节点pop出，优先进行判断和扩展。

4.运行结果

A*+不在位数码启发函数+hash+堆排序：

无结果

A*+Manhattan distance+hash+堆排序：

[[11  9  4 15] 
 [ 1  0  3 12] 
 [ 7  5  8  6] 
 [13  2 10 14]]
-------------------
[[11  0  4 15]
 [ 1  9  3 12]
 [ 7  5  8  6]
 [13  2 10 14]]
-------------------
...
-------------------
[[ 1  2  3  4]
 [ 5  6  7  0]
 [ 9 10 11  8]
 [13 14 15 12]]
-------------------
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11  0]
 [13 14 15 12]]
-------------------
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]
 [13 14 15  0]]
-------------------
Deepth: 41
NodeNum: 216338
Runtime: 5.981008 s