人工智能大作业——A*算法迷宫寻路问题
项目设计的目的
利用A*算法实现迷宫寻路功能,利用启发式函数的编写以及各类启发式函数效果的比较。
相关原理知识介绍
A*(A-Star)算法是一种静态路网中求解最短路最有效的方法。公式表示为:f(n)=g(n)+h(n),其中f(n)是节点n从初始点到目标点的估价函数,g(n)是在状态空间中从初始节点到n节点的实际代价,h(n)是从n到目标节点最佳路径的估计代价。保证找到最短路径(最优解的)条件,关键在于估价函数h(n)的选取:估价值h(n)小于等于n到目标节点的距离实际值,这种情况下,搜索的点数多,搜索范围大,效率低,但能得到最优解。如果估价值大于实际值,搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
启发式搜索:启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估,得到最好的位置,再从这个位置进行搜索直到目标。这样可以省略大量无畏的搜索路径,提到了效率。在启发式搜索中,对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。
估价函数:从当前节点移动到目标节点的预估费用;这个估计就是启发式的。在寻路问题和迷宫问题中,我们通常用曼哈顿(manhattan)估价函数(下文有介绍)预估费用。
A算法与BFS:可以这样说,BFS是A算法的一个特例。对于一个BFS算法,从当前节点扩展出来的每一个节点(如果没有被访问过的话)都要放进队列进行进一步扩展。也就是说BFS的估计函数h永远等于0,没有一点启发式的信息,可以认为BFS是“最烂的”A算法。(注解:不一定是0,读者只要认为是“相同的”就可以了)
选取最小估价:如果学过数据结构的话,应该可以知道,对于每次都要选取最小估价的节点,应该用到最小优先级队列(也叫最小二叉堆)。在C++的STL里有现成的数据结构priority_queue,可以直接使用。当然不要忘了重载自定义节点的比较操作符。
A算法的特点:A*算法在理论上是时间最优的,但是也有缺点:它的空间增长是指数级别的。
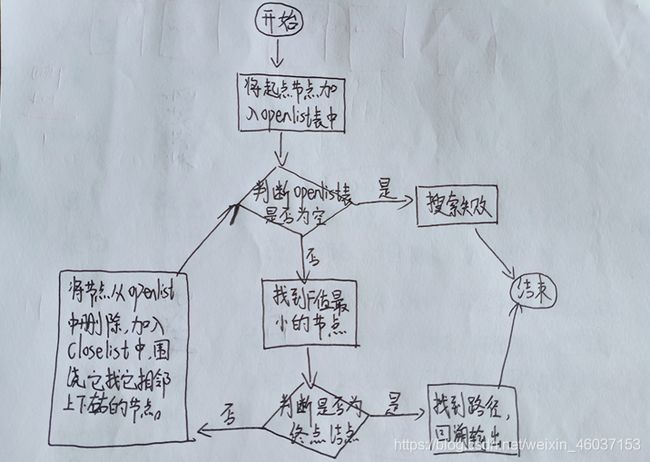
设计的求解问题的流程图的说明
A*算法寻路的求解步骤说明:
1.将起点方格(节点)加入openlist链表中,作为寻路开始的起点;
2.循环执行以下步骤,直到openlist链表为空结束或者终点(节点)加入到 openlist 中:
(1)在openlist中找到F值最小的那个节点(如果有相等的情况,就选择最先找到的那个节点)作为[ 当前节点 ];
(2)在openlist中将第1步找到的那个F值最小的节点,从openlist中删除掉;
(3)在closelist中将第1步找到的那个F值最小的节点,加入closelist中;
(4)围绕第1步找到的那个F值最小的 [ 当前节点 ] ,找到与它相邻的 四个方向(上下左右) 上的节点,这里要判断邻居节点的有效性,看 邻居节点 是否满足以下条件:
<1>邻居节点是否越界——节点的x或者y是否在可视范围内;
<2>邻居节点是否为障碍方格(节点)——比如本程序中的 MAZE[i][j]=1 即为障碍,MAZE[i][j]=0 即为可用;
<3>邻居节点是否已经在openlist链表中或者closelist链表中;
<4> 以上都满足就抛弃不要,否则这个邻居节点就要留下来,并进行初始化:
【1】指定[当前节点]为这个[邻居节点]的父节点;
【2】计算[邻居节点]的G值;
【3】计算[邻居节点] 的H值;
【4】计算[邻居节点]的F值;
<5>初始化完毕,将[邻居节点]加入openlist中;
3.如果找到了可寻的路径,利用节点的parent属性,回溯打印输出路径即可。
package graph;
import java.util.ArrayList;
import java.util.List;
//A*寻路算法简单实现————>四方向(上下左右)
public class Maze_A_ManHaDun {
//简单的迷宫模拟——利用二维数组,其中 1 表示障碍,不可通过。
public static final int[][] MAZE= {
{0, 1, 0, 0, 0, 0, 0},//7
{0, 0, 1, 0, 0, 0, 0},
{1, 0, 0, 1, 0, 0, 0},
{0, 1, 0, 1, 1, 1, 1},
{0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 1, 1, 0},
//7
};
//定义 方格节点——grid
static class Grid{
public int x;//结点
public int y;
public int f;//fn
public int g;//gn
public int h;//hn
public Grid parent;
public Grid(int x,int y) {
this.x=x;
this.y=y;
}
//实例化一个方格节点
public void initGrid(Grid parent, Grid end) {
//parent赋值
this.parent=parent;
//计算g的大小
if(parent!=null) {
this.g=parent.g+1;
//this.g=0;
}
else
{
this.g=1;
}
//计算h的大小
this.h=Math.abs(this.x-end.x)+Math.abs(this.y-end.y);
//this.h=Math.abs(this.x-end.x)*Math.abs(this.y-end.y);
//计算f的大小
this.f=this.g+this.h;
}
}
//寻路算法核心实现过程
public static Grid aStarSearch(Grid start, Grid end) {
//准备两个链表,分别存储 将要选择的节点 和 已经走过的节点
ArrayList<Grid> openlist=new ArrayList<Grid>();
ArrayList<Grid> closelist=new ArrayList<Grid>();
//将起点加入链表,准备开始寻路。
openlist.add(start);
//只要链表不为空,就重复这个寻路的过程
while(openlist.size()>0) {
//找到 openlist中 F值最小的那个 方格(节点)
Grid currentgrid=findMinGrid(openlist);
//从 openlist中删除找到的那个 F值 最小的那个节点
openlist.remove(currentgrid);
//将这个 F值 最小的节点,加入到 closelist 中
closelist.add(currentgrid);
//寻找 当前找到的这个 F值最小的节点的 邻居节点 ——上下左右,四个方向上的节点,要判断它们是否为合法可用的节点。
List<Grid> neighbors=findNeighbors(currentgrid, openlist, closelist);
//对合法可用的邻居节点进行初始化,并加入到 openlist中
for(Grid grid : neighbors) {
if(!openlist.contains(grid)) {
grid.initGrid(currentgrid,end);
openlist.add(grid);
}
}
//邻居节点加入 openlist 后,判断openlist中,是否包含 终点节点,如果包含终点,直接返回并退出。
for(Grid grid : openlist) {
if((grid.x==end.x) && (grid.y==end.y)) {
return grid;
}
}
}
return null;
}
//寻找邻居节点的方法,返回值为 链表 ——创建一个合理的邻居链表
private static ArrayList<Grid> findNeighbors(Grid grid, List<Grid> openlist, List<Grid> closelist) {
// TODO Auto-generated method stub
ArrayList<Grid> gridlist=new ArrayList<Grid>();
//判断上下左右邻居节点的合理性,没问题就加入到邻居链表中。
if(isValidGrid(grid.x, grid.y-1, openlist, closelist)) {//下
gridlist.add(new Grid(grid.x, grid.y-1));
}
if(isValidGrid(grid.x, grid.y+1, openlist, closelist)) {//上
gridlist.add(new Grid(grid.x, grid.y+1));
}
if(isValidGrid(grid.x-1, grid.y, openlist, closelist)) {//左
gridlist.add(new Grid(grid.x-1, grid.y));
}
if(isValidGrid(grid.x+1, grid.y, openlist, closelist)) {//右
gridlist.add(new Grid(grid.x+1, grid.y));
}
return gridlist;
}
//判断当前位置的节点是否合理
private static boolean isValidGrid(int x, int y, List<Grid> openlist, List<Grid> closelist) {
// TODO Auto-generated method stub
//当前节点是否越界,不再MAZE数组范围内了,注意二位数组的长度计算方法及含意
//MAZE。length表示行的长度
//MAZE[0]。length表示列的长度
if(x<0 || x>=MAZE.length || y<0 || y>=MAZE[0].length) {
return false;
}
//当前节点是否为障碍节点
if(MAZE[x][y]==1) {
return false;
}
//判断当前节点是否在 openlist中
if(containgrid(openlist, x, y)) {
return false;
}
//判断当前节点是否在 closelist中
if(containgrid(closelist, x, y)) {
return false;
}
return true;
}
//判断当前链表中是否包含当前的节点
private static boolean containgrid(List<Grid> grids, int x, int y) {
// TODO Auto-generated method stub
for(Grid grid : grids) {
if((grid.x==x) && (grid.y==y)) {
return true;
}
}
return false;
}
//寻找当前链表中的节点F值 最小的那个节点,并返回这个节点。
private static Grid findMinGrid(ArrayList<Grid> openlist) {
// TODO Auto-generated method stub
Grid tempgrid=openlist.get(0);
for(Grid grid : openlist) {
if(grid.f<tempgrid.f) {
tempgrid=grid;
}
}
return tempgrid;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
int b1=0,b2=0;//起始坐标
int c1=0,c2=6;
Grid startgrid=new Grid(b2,b1);
System.out.println("起点坐标为:"+"("+b1+","+b2+")");
Grid endgrid=new Grid(c2,c1);
System.out.println("终点坐标为:"+"("+c1+","+c2+")");
Grid resultgrid=aStarSearch(startgrid,endgrid);
//创建回溯链表
ArrayList<Grid> path=new ArrayList<Grid>();
while(resultgrid!=null) {
path.add(new Grid(resultgrid.x, resultgrid.y));
resultgrid=resultgrid.parent;
}
//打印输出当前寻路路径
int count=0;
for(int i=0; i<MAZE.length; i++) {
for(int j=0; j<MAZE[0].length; j++) {
if(containgrid(path, i, j)) {
System.out.print("走, ");
count++;
}
else
{
System.out.print(MAZE[i][j]+ ", ");
}
}
System.out.println();
}
System.out.println("最短路径长度为:"+count);
}
}
尝试改变启发式算法提高迷宫搜索速度
A算法的估价函数可表示为:f’(n) = g’(n) + h’(n)这里,f’(n)是估价函数,g’(n)是起点到节点n的最短路径值,h’(n)是n到目标的最短路经的启发值。由于这个f’(n)其实是无法预先知道的,所以我们用前面的估价函数f(n)做近似。g(n)代替g’(n),但 g(n)>=g’(n)才可(大多数情况下都是满足的,可以不用考虑),h(n)代替h’(n),但h(n)<=h’(n)才可(这一点特别的重要)。可以证明应用这样的估价函数是可以找到最短路径的,也就是可采纳的。我们说应用这种估价函数的最好优先算法就是A算法。
分析不同启发式函数对迷宫寻路速度的提升效果
g(n)和h(n)求解方法不同将直接影响A*算法的效率,好的解决方法不仅能够使路径变短,而且在求解过程中所搜索和产生的节点数也会尽量的少;而比较差的解决方法则可能导致所找到的路径未必是最短的,尽管它在求解过程中所搜索和产生的节点数也比较少。