【保姆级手写理解——灰色预测理论以及python实现】

写在前面

近日了解了一下灰色预测算法的原理，经过了不少的数理推导过程，因此本期的博客希望以一种“手写”的方式带领读者们感受这个国产玄学方法的推导过程。另外本文参照的是清风的数模新版视频课件第12讲预测模型，感兴趣的朋友们可以查找相关资料对灰色预测进行进一步的深入了解。

此外本文代码只是清风灰色预测模型中GM(1,1)和新陈代谢GM(1,1)模型的python版本复现。推荐使用anaconda中的Spyder软件进行验证！

笔者简介:CCNU计科，爱好游戏王，日漫op以及周董的歌，还有偶像梅老板。

灰色建模初衷

“由于数据列的离散性，信息时区内将出现空集（不包含信息的定时区），因此只能按近似的微分方程条件，建立近似的，不完全确定的微分方程模型”

我们应该怎么理解呢？简而言之，我们就是要对数列建立近似的微分方程模型，但是由于微分方程的适合函数首先要满足可微的条件，但是一个时间序列的数据不是连续的，可导不一定连续，连续一定不可导！，参照高数的概念理解我们知道可导和可微是大致一致的。不可导的函数也就不可微分。

因此我们要想建立灰色预测模型，得到的只能是一个近似的微分方程。在《灰色系统理论教程》中我们称之为"灰色微分方程"。

OLS原理（普通最小二乘法）

现在假设你开始对一系列的时间序列数据进行拟合和预测，我们需要研究一组变量xi和yi之间的联系。现在无论时间序列多么松散，你想用一条直线来预测，所以你自信的写了这个公式:

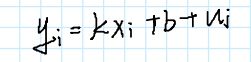
嗯?为什么后面要加一个ui呢?你说，这个ui就是衡量我的函数得到的预测值与序列实际值之间的差距，还可以叫做“残差”。

“另外，为了使得这个ui最小，我考虑使用类似损失函数的概念思想，来确定k和b的预测值。我还看到了argmin的一个概念:使目标函数f(x)取最小值时的变量值”!因此我写得表达式如下:

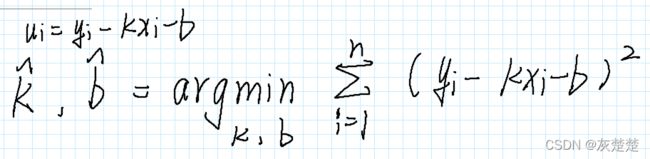
现在我们要利用向量化的思想，将这个表达式表示为矩阵乘积的形式，这有何难？你也刷刷几笔潇洒地写了出来:

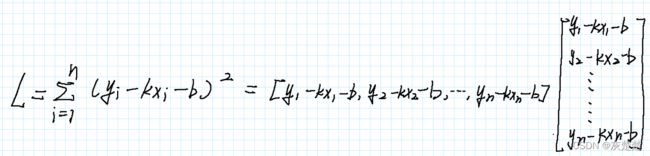
这个时候，你说，我们该怎么求解k和b呢？先不着急，咱们好不容易见到线性代数，和它好好玩玩呗。于是我们可以将矩阵再矩阵化:

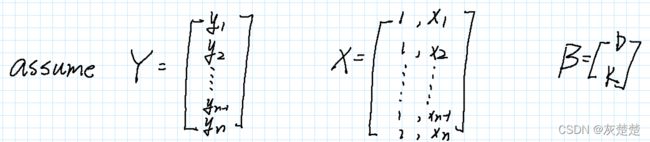
如上假设后，我们就可以利用Y,X,beta 将我们的损失函数表达式表示:


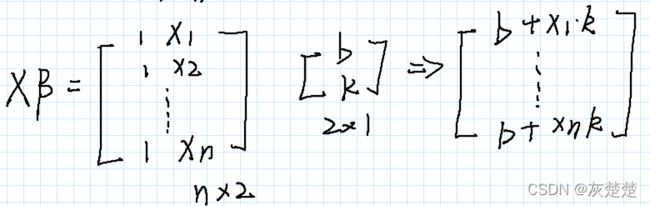
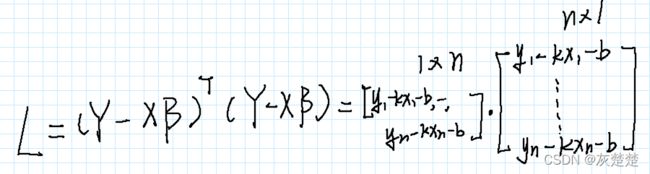
这时候，你说，线性代数的转置罢了，我来，于是乎我们展开表达式如下:

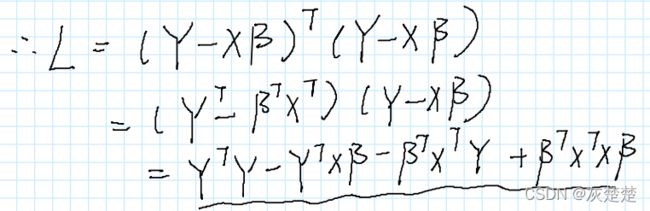
请记住，我们这里面的beta包含的其实就是要求解的两个参数，我们应该怎么求呢，显然，利用L对于beta的偏导数等于0，这样的话我们可以建立beta和X,Y的关系表达式从而得到L的极小值，但是但是，这里是矩阵的求导，我们该怎么办呢？

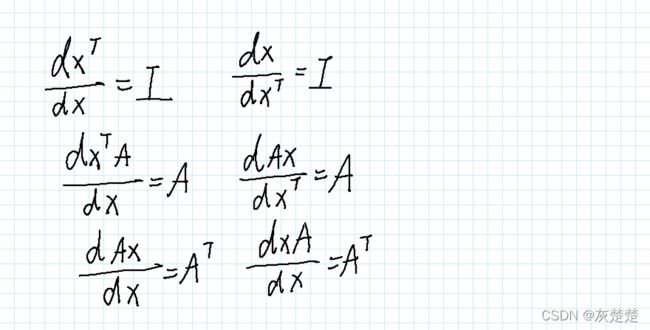
以上是常用的矩阵求导公式，可以记忆一下，详细的证明请参考以下链接:
(矩阵求导理论推导过程的链接文章)
于是我们利用上述的表达式开始求导计算:

在假设可逆成立的前提下，我们可以得到beta的表达式如下:

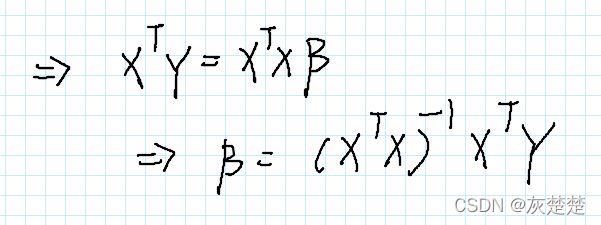
由此我们就可以计算出所求的参数k和b，这也就是GM(1,1)模型的开端。

GM(1,1)原理介绍

现在我们已经知道了k和b怎么求，问题是什么作为我们的自变量x与y呢?现在我们看看一组时间序列数据:

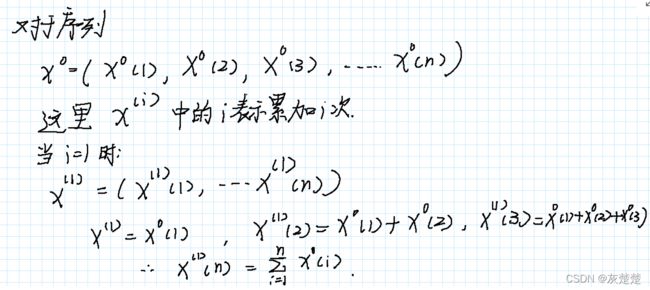
我们研究的是序列的累加问题，由上述公式我们可以得到x0序列的第一次累加和序列，紧随其后的就是求得x1的紧邻均值序列z1：

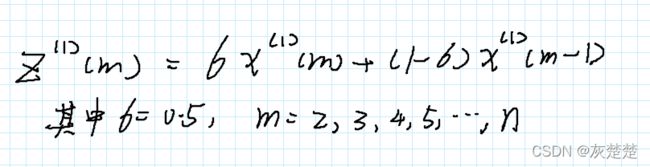
灰色预测的思路就是将z1作为自变量，x0作为因变量,建立一个函数关系表达式:

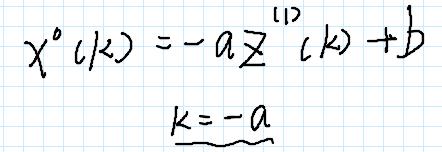
接下来我们将x0转换成为x1的差的形式表达,可以手写如下:

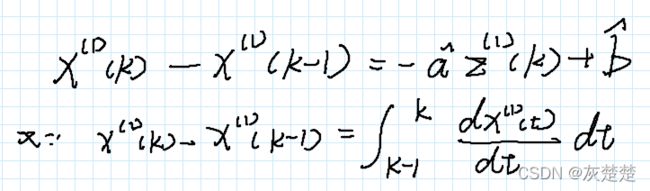
利用牛顿–莱布尼兹公式我们可以将x1表示成如上的积分形式，这时候我们再带入z1的表达式形式:

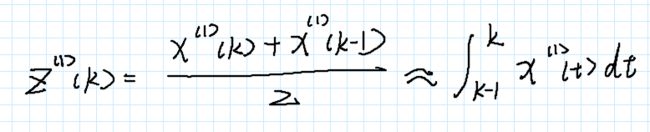
等等，为什么会是这样的形式呢?也许我们需要简单的画个图理解一下:

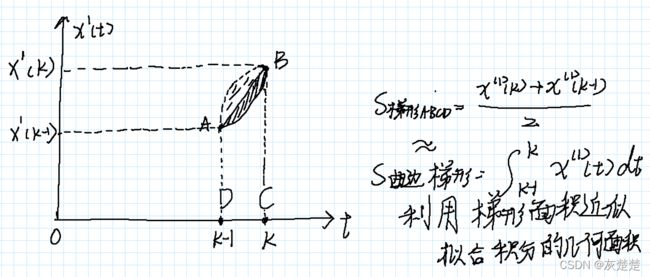
类比手写的方法，我们利用积分的表达形式近似拟合梯形的面积大小也就是紧邻均值z1，从而我们可以得到如下的等式:
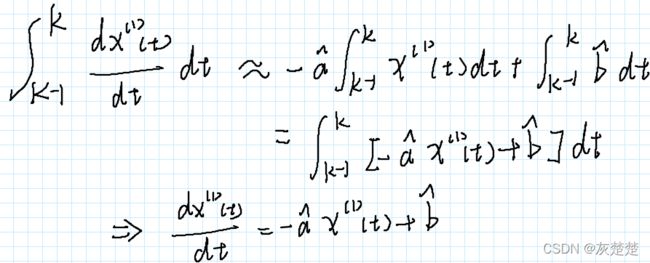这是我们箭头所指向的就是x1关于时间的微分方程模式:

d x(1)(t) / dt = - a * x(1)(t) + b

这就被称为GM(1,1)模型的白化方程,而我们用来回归x0和z1的方程则被称为灰色微分方程。

发展系数与预测情形的探究

如果我们得到了白化微分方程和其初始值，现在要求解此微分方程，步骤如下:

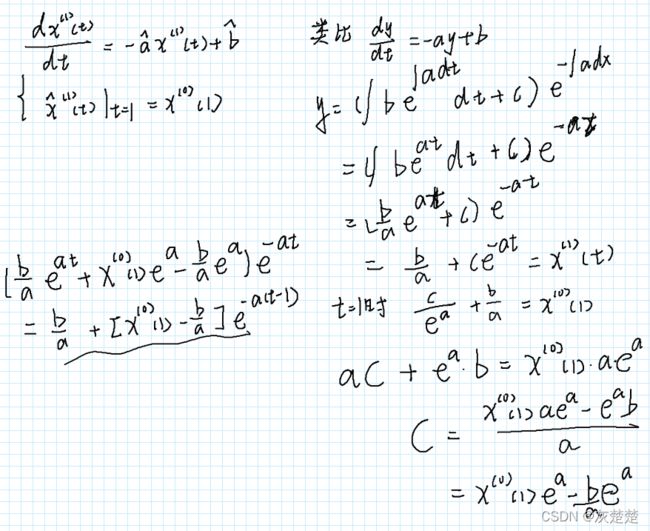
又因为累加数列和原始时间序列的关系，我们将x1转化成为x0的表达形式:(注意更正:图中m=1,2,3,4,…,n-1)

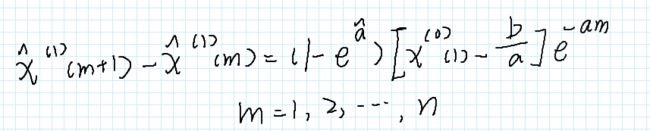
若要对原始数据进行预测的话，只需要上等式取m>=n即可。

GM(1,1)模型的评价

对于利用GM(1,1)模型对未来数据与测试，我们一般利用以下两种方法检验GM模型对于原始数据的拟合程度(也就是对原始数据换元的效果)

残差检验

级比偏差检验

GM(1,1)模型的拓展

什么时候使用?(智者看法)

借用清风的看法总结如下:

1.数据是按照年份度量的非负数据。

2.数据能经过准指数规律检验。

3.数据的期数较短且和其他数据之间的关联性不强。如果数据期数较长，一般用传统的时间序列模型会比较合适。

代码区

GM(1,1)和新陈代谢型GM(1,1)的实现。在Spyder中一个一个**# In[]元胞板块点击右键运行即可**(中间有输入数据的部分输入即可)

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
import pandas as pd
# In[]
def gm11(x,n):
    nn=len(x)
    x1=np.cumsum(x)#第一次累加
    z1=(x1[:len(x1)-1]+x1[1:])*1.0/2.0 #紧邻均值
    yy=x[1:]
    xx=z1
    k = ((nn-1)*np.sum(xx*yy)-np.sum(xx)*np.sum(yy))/((nn-1)*np.sum(xx*xx)-np.sum(xx)*np.sum(xx))
    b = (np.sum(xx*xx)*np.sum(yy)-np.sum(xx)*np.sum(xx*yy))/((nn-1)*np.sum(xx*xx)-np.sum(xx)*np.sum(xx))
    a=-k
    print(a,b)
    
    if np.abs(a)>2:
        print("没有意义")
    elif np.abs(a)<=2:
        print("有意义")
        if 0.3<-a<=0.5:
            print("适用于短期预测")
        elif 0.5<-a<=0.8:
            print("对于短期数据谨慎使用!")
        elif 0.8<-a<=1.0:
            print("应该对此模型进行修正!")
        elif -a>1.0:
            print("不宜使用GM(1,1)模型预测!")
        else:
            print("适用于中期和长期预测")
            
    x0_hat=np.zeros(nn)
    x0_hat[0]=x[0]
    
    for m in range(nn-1):
        x0_hat[m+1]=(1-np.exp(a))*(x[0]-b/a)*np.exp(-a*m)#预测的x0
    result=np.zeros(n)
    
    for i in range(n):
        result[i]=(1-np.exp(a))*(x[0]-b/a)*np.exp(-a*(nn+i))
        
    absolute_residuals = x[1:] - x0_hat[1:]#计算绝对残差和相对残差
    relative_residuals = np.abs(absolute_residuals) / x[1:]
    
    class_ratio = x[1:]/x[:len(x)-1] #计算级比和级比偏差
    eta = np.abs(1-(1-0.5*a)/(1+0.5*a)*(1/class_ratio))
    
    return result,x0_hat,relative_residuals,eta
# In[]
def metabolism_gm11(x0,predict_num):
    result=np.zeros(predict_num)
    for i in range(predict_num):
        temp=gm11(x0,1)
        result[i]=temp[0][0]
        x0=x0[1:]
        x0=np.append(x0,temp[0][0])
    return result,temp[1],temp[2],temp[3]

# In[]

print("请输入一系列数据(少于10个):")
arr = input("")    
num = [float(n) for n in arr.split()]   
data=np.array(num)
print(data)

# In[]

print("输入数据检验:")
data1=np.cumsum(data)
rho=data[1:]/data1[:-1]
print(f"光滑比例小于0.5的数据占比为{100*np.sum(rho<0.5)/(len(data)-1)}%")
print(f"除去前两个时期光滑比小于0.5的数据占比为{100*np.sum(rho[2:]<0.5)/(len(data)-3)}")
if 100*np.sum(rho<0.5)/(len(data)-1) >60  and 100*np.sum(rho[2:]<0.5)/(len(data)-3) > 90:
    print("可以")
else:
    print("不可以")


# In[]
originlen=len(num)
second=np.arange(len(num)+3)+1#这里的3也就是预测天数，可以自行修改
result1=gm11(data,3)#这里的3也就是预测天数，可以自行修改
a=result1[0]#预测结果

print(result1[0])
print(f"拟合效果评价{np.mean(result1[2])}")

if 0.1<np.mean(result1[2])<0.2:
    print("达到一般要求")
elif np.mean(result1[2])<=0.1:
    print("拟合效果非常不错!")
else:
    print("垃圾")
print(f"平均级比偏差{np.mean(result1[3])}")


if 0.1<np.mean(result1[3])<0.2:
    print("达到要求一般")
elif np.mean(result1[3])<=0.1:
    print("拟合效果非常不错!")
else:
    print("垃圾")
    
num1=num[:]
for i in range(len(a)):
    num.append(a[i])
print(num)

plt.plot(second,num)
plt.xlabel("样本数加预测周期数")
plt.ylabel("数值")
plt.title("灰色预测GM(1,1)原始版")
plt.grid()
plt.show()

# In[]
result2=metabolism_gm11(data, 3)
b=result2[0]

print(result2[0])
print(f"拟合效果评价{np.mean(result2[2])}")

if 0.1<np.mean(result2[2])<0.2:
    print("达到一般要求")
elif np.mean(result2[2])<=0.1:
    print("拟合效果非常不错!")
else:
    print("垃圾")
    
    
print(f"平均级比偏差{np.mean(result2[3])}")
if 0.1<np.mean(result2[3])<0.2:
    print("达到要求一般")
elif np.mean(result2[3])<=0.1:
    print("拟合效果非常不错!")
else:
    print("垃圾")
    
for i in range(len(b)):
    num1.append(b[i])
print(num1)
# In[]
plt.plot(second,num1)
plt.grid()
plt.xlabel("样本数加预测周期数")
plt.ylabel("数值")
plt.title("新陈代谢灰色预测GM(1,1)原始版")
plt.show()