【深度学习】基本的CNN算子

CNN是经典的深度学习神经网络。从LeNet-5中涉及到的算子开始，尝试将CNN网络分解来看，在具体分析针对性的网络结构前，有助于我们见微知著，更直观地把握住模型演化的规律。

因为经典网络LeNet-5涵盖的是卷积神经网络中最基本的卷积层、激活层、池化层和全连接层，故本文欲以此为例，对CNN网络中这几个基本的层算子先进行分析，以抓住CNN网络的核心。随着卷积神经网络的发展，又有反卷积层、批量归一化（BN）层和Shortcut等层提出，这些新提出的层算子使得深度神经网络在解决图像处理和其他复杂问题上更快速、更高效，在此先按下不表。

下面这幅图来自：LeNet-5网络详解

在CNN中，特定层的特征值仅连接到前一层中的局部空间区域，并且在图像的整个空间占用中具有一致的共享参数集，即局部感知和共享参数， 其模拟了人类识别物体时人脑的工作原理——单个皮层神经元只对空间中某个受限区域的刺激做出反应（即感受野）。

卷积算子

卷积运算的目的是从图像中提取信息或特征。 任何一个图像都可以看作一个数值矩阵，而矩阵中的一组特定的数字可以构成一个特征。卷积运算的目的是扫描这个矩阵，并尝试为图像挖掘相关的或可解释性特征。因为特征映射是基于核和原输入图像上对应像素之间的对应元素相乘获得的，所以每次改变核的数值都会产生不同的特征映射。

卷积算子中重要的概念有：

1. 卷积核（Kernel）。图像处理时，对输入图像中一个小区域像素加权平均后成为输出图像的一种操作。其中，权值由一个函数定义，这个函数便被称为卷积核，直观理解就是一个滤波矩阵。 普遍使用的卷积核大小为3×3、5×5等。
2. 填充（Padding）。填充是指处理输入特征图（Feature Map）边界的方式。为了不丢弃原图信息，让更深层的输入依旧保持有足够大的信息量，往往会先对输入特征图边界外进行填充（一般填充为0），再执行卷积操作。Padding操作可以使输出特征图的尺寸不会太小，或者与输入特征图的尺寸一致。
3. 步长（Stride）。步长即卷积核遍历输入特征图时每步移动的像素数。如步长为1，则每次移动1个像素；步长为2，则每次移动2个像素（即跳过1个像素）。
4. 输出特征图尺寸。定义输入特征图尺寸为$I$，卷积核尺寸为$K$，滑动步长为$S$，填充像素数为$P$，输出特征图尺寸为$O$，则

$$O=\lfloor \frac{I-K+2P}{S}\rfloor +1$$

下面以3×3的数据矩阵 $I$ 采用3×3的卷积核$K$ 为例，来说明卷积算子的具体运算过程：

下面展示了使用一个卷积核来得到一个特征图的过程，实际应用中，会使用多个卷积核得到多个输出特征图。用不同颜色框表示从输入特征图矩阵中依次提取出和卷积核一样大小的块数据。为了提高卷积操作的运算效率，需要进行img2col（图像矩阵转换成列）操作，即把这些不同颜色框内的数据向量化，共有3×3个向量，最后得到9个向量化的数据矩阵。于此同时，将卷积核展成行，准备与图像矩阵展成的列进行矩阵相乘。如下图所示

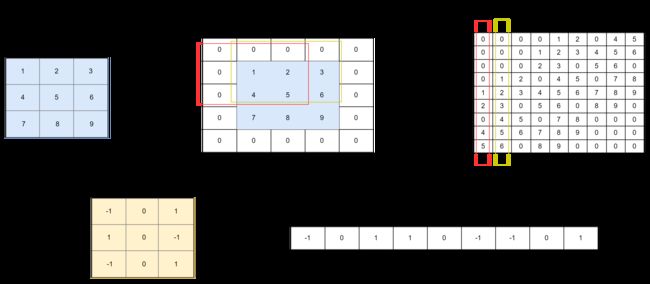
通过矩阵乘法，将得到特征矩阵的输出，最后进行col2img（矩阵转特征图）操作，将生成的列向量转成矩阵输出，从而得到特征图。如下图所示

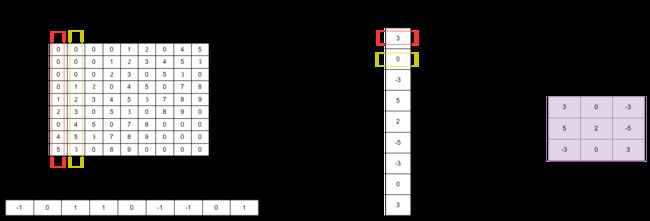
以上就是卷积算子通过img2col方式完成特征图矩阵卷积的具体过程。如果按照数学中的步骤做卷积，则在操作时读取的内存是不连续的，这样会增加时间成本。而卷积对应元素相乘再相加的做法跟向量内积很相似，所以通过img2col将矩阵卷积转化为矩阵乘法来实现，可大大提高矩阵卷积的速度。

这里只给出了一个卷积核，一个卷积核只会生成一个特征图，而在实际应用中，为了增强卷积层的表达能力，会使用很多个卷积核以得到多个特征图（如LeNet-5中就选择了6个卷积核）。卷积核很多时，如果一个一个计算会很浪费时间和内存，但是如果把这些卷积核全部按行排列，再与输入特征图转成的列向量作矩阵相乘操作，会一次得出所有的输出特征图，这样可大大提高特征图矩阵卷积的速度。

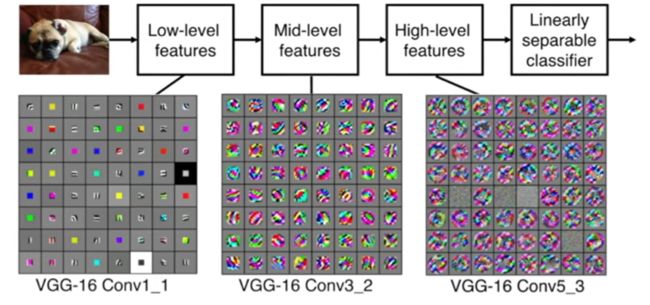
另外值得关注的是，对于卷积逐层提取特征的可视化解释 ，Matthew D. Zeiler和Rob Fergus的论文《Visualizing and Understanding Convolutional Networks》对此有一个很好的说明，下面这张图片来自李飞飞的cs231n课程介绍CNN的部分：其反映的正是卷积逐层从浅层特征（如边缘）到深层特征（如类别）的过程。

激活算子

激活算子一般接在卷积层或全连接层后，其可以激活神经网络某一部分神经元，并将激活信息向后传入下一层的神经网络。激活算子的意义是为高度线性的神经网络引入非线性运算，让神经网络具备强大的拟合能力。激活算子不会改变数据的维度，即输入和输出的维度是相同的。激活算子一般用特定函数表示，并成为激活函数。 激活函数的种类很多，下面列举一些常见的基本函数

函数名称	Sigmoid 函数	Tanh 函数	ReLU 函数	Softmax 函数
计算公式	$$S(x)=\frac{1}{1+e^x}$$	$$tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$$	$$ReLU(x)=max(x,0)$$	$$\sigma (z{)}_j=\frac{e^{z_j}}{{\sum }_i{e}^{z_i}}{z}^i表示第i个输出值$$

其中ReLU函数是神经网络中经常使用的激活函数，基于ReLU，有LeakyReLU、ELU、SeLU等一系列变式；Softmax作为一种特殊的激活函数，往往用于分类型神经网络的输出层，旨在输出输入样本属于各个类别的概率。

激活函数设计需考虑的因素：

1. 非线性：当激活函数是非线性的，一个两层神经网络可以证明是一个通用函数近似值，如果失去了非线性，整个网络就相当于一个单层的线性模型。
2. 连续可微性：这个属性对基于梯度优化方法是必要的，如果选择了一些具有局部不可微的函数，则需要强行定义此处的导数。
3. 有界性：如果激活函数有界的，基于梯度的训练方法往往更稳定；如果是无界的，训练通常更有效率，但是训练容易发散，此时可以适当减小学习率。
4. 单调性：如果激活函数是单调的，与单层模型相关的损失函数是凸的。
5. 平滑性：有单调导数的平滑函数已经被证明在某些情况下泛化效果更好。

池化算子

池化算子是神经网络中的池化层算子，作为一种下采样算子，旨在通过降低特征图的分辨率获得具有空间不变性的特征。池化算子在整个网络结构中起到二次提取特征的作用，它的每个神经元对局部接收域进行池化操作，从而降低特征图尺寸和网络模型的计算量 。常用的池化算子有

1. 平均池化算子：对局部感受野中的所有值求均值并作为采样值
2. 最大池化算子：取局部感受野中的最大值作为采样值

假设输入矩阵大小为2，池化算子的 stride = 2, pad = 0，下图展示了这两者的区别

全连接算子

卷积层、池化层和激活层（如ReLU层）通常交织在神经网络中以提高网络的表达能力。激活层通常在卷积层之后，与传统神经网络中非线性激活函数通常在线性点积后一样。因此，卷积层和激活层通常一个接一个地黏在一起，一些神经架构（如AlexNet）就因此没有显式地显示激活层，因为它们被认为总是粘在线性卷积层的末段。在两组或三组卷积层和激活层之后，可能有一个最大池化层。这样的模式重复三次后，在最后加一个全连接层，构成的神经网络就类似于
$$CRCRPCRCRPCRCRPF$$

与多层感知器类似，全连接层中的每个神经元与其上一层中的所有神经元相连，据此，全连接算子可以整合卷积层或池化层中具有类别区别性的局部信息。在全连接网络中，将所有二值图像的特征图拼接为一维特征并作为全连接特征图拼接为一维特征并作为全连接层的输入，全连接层对输入进行加权求和后送入激活层。

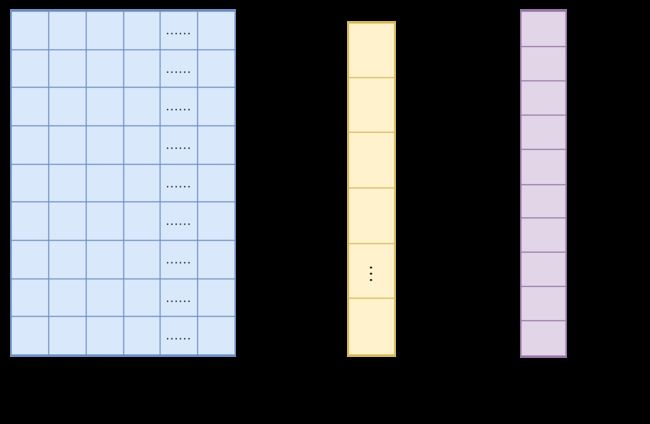
下面展示了全连接层的过程

X是全连接层的输入，也就是特征； W是全连接层的参数，也称为权值。特征X是全连接层前面多个卷积层和池化层处理后得到的。假如全连接层前面连接的是一个卷积层，这个卷积层输出了100个特征（即特征图通道为100），每个特征的大小为4×4，在将100个特征输入给全连接层之前Flatten层会将这些特征拉平成N行1列的一维向量，此时，$N=100\times 4\times 4=1600$，则特征向量X为1600行1列的一维向量。

全连接层的参数W是深度神经网络训练过程中全连接层寻求的最优权值，可表示为T行N列的二维向量，其中T表示类别数。例如，需要解决的是7分类问题，则T=7，其他分类数以此类推。通过$W\times X=Y$，得到T行1列的一维向量，即为全连接层的输出。

---

[1]《神经网络与深度学习》第8章 卷积神经网络，机械工业出版社
[2]《深度神经网络FPGA设计与实现》第3章 深度神经网络基础层算子介绍，西安电子科技大学出版社
[3]《深度学习案例精粹》第7章 卷积神经网络，人民邮电出版社