多任务学习 (Multitask Learning) 汇总

1 前言

        多任务学习（Multi-task learning）是和单任务学习（single-task learning）相对的一种机器学习方法。在机器学习领域，标准的算法理论是一次学习一个任务，也就是系统的输出为实数的情况。复杂的学习问题先被分解成理论上独立的子问题，然后分别对每个子问题进行学习，最后通过对子问题学习结果的组合建立复杂问题的数学模型。多任务学习是一种联合学习，多个任务并行学习，结果相互影响。

        拿大家经常使用的school data做个简单的对比，school data是用来预测学生成绩的回归问题的数据集，总共有139个中学的15362个学生，其中每一个中学都可以看作是一个预测任务。单任务学习就是忽略任务之间可能存在的关系分别学习139个回归函数进行分数的预测，或者直接将139个学校的所有数据放到一起学习一个回归函数进行预测。而多任务学习则看重任务之间的联系，通过联合学习，同时对139个任务学习不同的回归函数，既考虑到了任务之间的差别，又考虑到任务之间的联系，这也是多任务学习最重要的思想之一。

        在机器学习中，我们通常关心优化某一特定指标，不管这个指标是一个标准值，还是企业KPI。为了达到这个目标，我们训练单一模型或多个模型集合来完成指定得任务。然后，我们通过精细调参，来改进模型直至性能不再提升。尽管这样做可以针对一个任务得到一个可接受得性能，但是我们可能忽略了一些信息，这些信息有助于在我们关心的指标上做得更好。具体来说，这些信息就是相关任务的监督数据。通过在相关任务间共享表示信息，我们的模型在原始任务上泛化性能更好。这种方法称为多任务学习（Multi-Task Learning），是本博文的关注点。

        多任务学习有很多形式，如联合学习（Joint Learning），自主学习（Learning to Learn），借助辅助任务学习（Learning with Auxiliary Tasks）等，这些只是其中一些别名。概括来讲，一旦发现正在优化多于一个的目标函数，你就可以通过多任务学习来有效求解（Generally, as soon as you find yourself optimizing more than one loss function, you are effectively doing multi-task learning (in contrast to single-task learning)）。在那种场景中，这样做有利于想清楚我们真正要做的是什么以及可以从中得到一些启发。

        即使对于最特殊的情形下你的优化目标只有一个，辅助任务仍然有可能帮助你改善主任务的学习性能。Rich Caruana 在文献[1]中总结了：“多任务学习通过使用包含在相关任务的监督信号中的领域知识来改善泛化性能”。通过学习本博文，我们将尝试对多任务学习的研究近况做一个简要的回顾，尤其是针对深度神经网络的多任务学习。首先，我们探讨了多任务学习的灵感来源。接下来，介绍多任务学习的两种最常见的方法。接着描述了使得多任务学习在实践中有效的机制。在总结较为高级的基于神经网络的多任务学习方法之前，我们回顾了以往多任务学习文献中的一些背景知识。本文接着介绍了近年来提出的一些给力的基于深度神经网络的多任务学习方法。最后，我们探讨了经常使用的辅助任务的类型以及对于多任务学习讲好的辅助任务所具备的特征。

        多任务学习早期的研究工作源于对机器学习中的一个重要问题，即“归纳偏置(inductive bias)”问题的研究。机器学习的过程可以看作是对与问题相关的经验数据进行分析，从中归纳出反映问题本质的模型的过程。归纳偏置的作用就是用于指导学习算法如何在模型空间中进行搜索，搜索所得模型的性能优劣将直接受到归纳偏置的影响，而任何一个缺乏归纳偏置的学习系统都不可能进行有效的学习。不同的学习算法(如决策树，神经网络，支持向量机等)具有不同的归纳偏置，人们在解决实际问题时需要人工地确定采用何种学习算法，实际上也就是主观地选择了不同的归纳偏置策略。一个很直观的想法就是，是否可以将归纳偏置的确定过程也通过学习过程来自动地完成，也就是采用“学习如何去学(learning to learn)”的思想。多任务学习恰恰为上述思想的实现提供了一条可行途径，即利用相关任务中所包含的有用信息，为所关注任务的学习提供更强的归纳偏置。

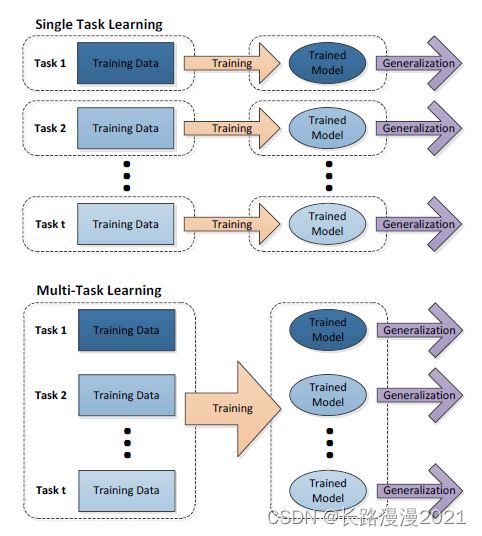
        看上面单任务学习和多任务学习的结构对比，可以发现单任务学习时，各个任务之间的模型空间（Trained Model）是相互独立的；而多任务学习时，多个任务之间的模型空间（Trained Model）是共享的。

        目前多任务学习方法大致可以总结为两类，一是不同任务之间共享相同的参数（common parameter），二是挖掘不同任务之间隐藏的共有数据特征（latent feature）。

---

2 动机

        我们提出多任务学习的出发点是多种多样的：

• （1）从生物学来看，我们将多任务学习视为对人类学习的一种模拟。为了学习一个新的任务，我们通常会使用学习相关任务中所获得的知识。例如，婴儿先学会识别脸，然后将这种知识用来识别其他物体。
• （2）从教学法的角度来看，我们首先学习的任务是那些能够帮助我们掌握更复杂技术的技能。这一点对于学习武术和编程来讲都是非常正确的方法。具一个脱离大众认知的例子，电影Karate Kid中Miyagi先生教会学空手道的小孩磨光地板以及为汽车打蜡这些表明上没关系的任务。然而，结果表明正是这些无关紧要的任务使得他具备了学习空手道的相关的技能。
• （3）从机器学习的角度来看，我们将多任务学习视为一种归纳迁移（inductive transfer）。归纳迁移（inductive transfer）通过引入归纳偏置（inductive bias）来改进模型，使得模型更倾向于某些假设。举例来说，常见的一种归纳偏置（Inductive bias）是$L_1$正则化，它使得模型更偏向于那些稀疏的解。在多任务学习场景中，归纳偏置（Inductive bias）是由辅助任务来提供的，这会导致模型更倾向于那些可以同时解释多个任务的解。接下来我们会看到这样做会使得模型的泛化性能更好。

---

3 深度学习中两种多任务学习模式

        工业界离散特征（ID类等）往往会转换成embedding，而推荐模型中embedding部分就占据着相当大的参数规模和计算量。做多任务时，如果各任务都需要embedding映射，那么每个任务都有一个独立的sparse映射表会非常的占用资源，所以底层参数（embedding、nn）共享在多任务学习中很是常见。

        前面我们讨论了多任务学习的理论源泉。为了使得多任务学习的思想更加具体，我们展示在基于深度神经网络的多任务学习中常用两种方法：隐层参数的硬共享与软共享。

• （1）参数的硬共享机制： 参数的硬共享机制是神经网络的多任务学习中最常见的一种方式，这一点可以追溯到文献[2]。一般来讲，它可以应用到所有任务的所有隐层上，而保留任务相关的输出层。硬共享机制降低了过拟合的风险。事实上，文献[3]证明了这些共享参数过拟合风险的阶数是N，其中N为任务的数量，比任务相关参数的过拟合风险要小。直观来将，这一点是非常有意义的。越多任务同时学习，我们的模型就能捕捉到越多任务的同一个表示，从而导致在我们原始任务上的过拟合风险越小。(此方法已经有快30年<1993>）
• （2）参数的软共享机制： 每个任务都由自己的模型，自己的参数。我们对模型参数的距离进行正则化来保障参数的相似。文献[4]使用L2距离正则化，而文献[5]使用迹正则化（trace norm）。用于深度神经网络中的软共享机制的约束很大程度上是受传统多任务学习中正则化技术的影响。我们接下来会讨论。（现代研究重点倾向的方法）
• （3）自定义共享：不同任务的底层模块不仅有各自独立的输出，还有共享的输出。

---

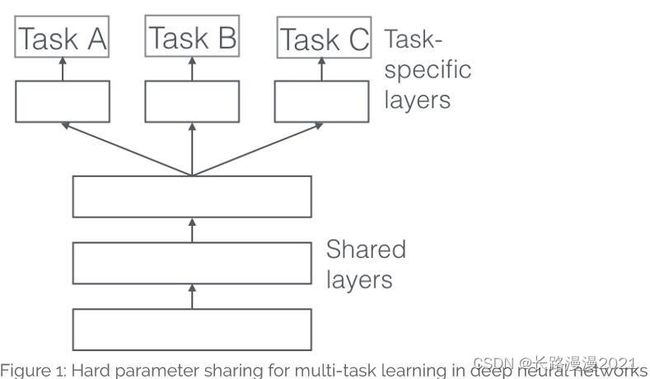
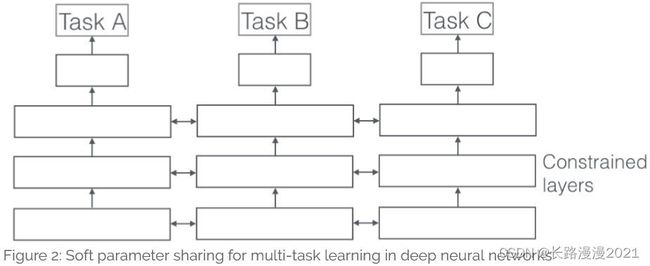
4 多任务学习为什么会有效？

        即使从多任务学习中获得归约偏置的解释很受欢迎，但是为了更好理解多任务学习，我们必须探究其深层的机制。大多数机制早在1998年被Caruana提出。为了便于距离说明，我们假设有两个相关的任务A与B，两者共享隐层表示F。

• （1）隐式数据增加机制。 多任务学习有效的增加了训练实例的数目。由于所有任务都或多或少存在一些噪音，例如，当我们训练任务A上的模型时，我们的目标在于得到任务A的一个好的表示，而忽略了数据相关的噪音以及泛化性能。由于不同的任务有不同的噪音模式，同时学习到两个任务可以得到一个更为泛化的表示（As different tasks have different noise patterns, a model that learns two tasks simultaneously is able to learn a more general representations.）。如果只学习任务A要承担对任务A过拟合的风险，然而同时学习任务A与任务B对噪音模式进行平均，可以使得模型获得更好表示F。
• （2）注意力集中机制。 若任务噪音严重，数据量小，数据维度高，则对于模型来说区分相关与不相关特征变得困难。多任务有助于将模型注意力集中在确实有影响的那些特征上，是因为其他任务可以为特征的相关与不相关性提供额外的证据。
• （3）特征信息窃取。 对于任务B来说很容易学习到某些特征G，而这些特征对于任务A来说很难学到。这可能是因为任务A与特征G的交互方式更复杂，或者因为其他特征阻碍了特征G的学习。通过多任务学习，我们可以允许模型窃听（eavesdrop），即使用任务B来学习特征G。最简单的实现方式是使用hints[6]，即训练模型来直接预测哪些是最重要的特征。
• （4）表示偏置机制。 多任务学习更倾向于学习到一类模型，这类模型更强调与其他任务也强调的那部分表示。由于一个对足够多的训练任务都表现很好的假设空间，对来自于同一环境的新任务也会表现很好，所以这样有助于模型展示出对新任务的泛化能力[7]
• （5）正则化机制。 多任务学习通过引入归纳偏置（inductive bias）起到与正则化相同的作用。正是如此，它减小了模型过拟合的风险，同时降低了模型的Rademacher复杂度，即拟合随机噪音的能力。

---

5 传统方法中多任务学习

        为了更好地了解深度神经网络中的 MTL，我们将研究关于 MTL 在线性模型、核函数方法和贝叶斯算法方面的论文。特别地，我们将讨论一直以来在多任务学习的历史中普遍存在的两个主要思想：通过范数正则化制造各任务间的稀疏性；对任务间的关系进行建模。

        请注意，许多 MTL 的论文具有同构性假设：它们假设所有任务与单个输出相关，例如，多类 MNIST 数据集通常被转换为 10 个二进制分类任务。最近的方法更加接近实际，对问题进行异构性假设，即每个任务对应于一组唯一的输出。

5.1 块稀疏（block-sparse）正则化

        为了更好地与下面的方法衔接，我们首先介绍一些符号。我们有$T$个任务。对于每个任务$t$，我们有一个模型$m_t$，其参数$a_t$的维度是 $d$。我们可以将参数作为列向量写出$a_t=[a_{1,t}...a_{d,t}{]}^{\top }$。我们现在逐列地将这些列向量$a_1,...,a_T$进行堆叠，形成矩阵 $A\in R^{d\times T}$。$A$的第$i$行包含与每个任务的模型的第$i$个特征对应的参数$a_{i,.}$，而$A$的第$j$列包含对应于第$j$个模型的参数 $a_{.,j}$。

        许多现有的方法对模型的参数做了稀疏性假设。例如，假设所有模型共享一小组特征 [8]。对我们任务的参数矩阵$A$来说，这意味着除了几行之外，所有数据都是 0，对应于所有任务只共同使用几个特性。为了实现这一点，他们将 $L_1$ 范数推广到 MTL。回想一下，$L_1$ 范数是对参数之和的约束，这迫使除几个参数之外的所有参数都为 0。这也被称为 lasso（最小绝对收缩与选择算子）。

        在单任务中，$L_1$ 范数根据相应任务 $t$ 的参数向量 $a_t$ 被计算，在 MTL 中，我们在任务参数矩阵 $A$ 中计算它。为了做到这一点，我们首先对每行 $a_i$ 计算出包含与第 $i$ 个特征相对应的参数的 $L_q$ 范数，其产生向量 $b=[\Vert a_1{\Vert }_q...\Vert a_d{\Vert }_q]\in R^d$。然后，我们计算该向量的 $L_1$ 范数，这迫使 $b$（即 A 矩阵的行）中除少数元素（entry）外，所有元素都为 0。

        可以看到，根据我们希望对每一行的约束，我们可以使用不同的 $Lq$。一般来说，我们将这些混合范数约束称为 $L_1/L_q$ 范数，也被称为块稀疏正则化，因为它们导致 $A$ 的整行被设置为 0。[9] 使用 $L_1/L_{\infty }$ 正则化，而 Argyriou 等人（2007）使用混合的 $L_1/L_2$ 范数。后者也被称为组合 lasso（group lasso），最早由[10]提出。

        Argyriou 等人（2007）也表明，优化非凸组合 lasso 的问题可以通过惩罚 $A$ 的迹范数（trace norm）来转化成凸问题，这迫使 $A$ 变成低秩（low-rank），从而约束列参数向量 $a_{.,1}，...，a_{.,t}$ 在低维子空间中。[11]进一步使用组合 lasso 在多任务学习中建立上限。

        尽管这种块稀疏正则化直观上似乎是可信的，但它非常依赖于任务间共享特征的程度。[12] 显示，如果特征不重叠太多，则 $L_l/L_q$ 正则化可能实际上会比元素一般（element-wise）的 $L_1$ 正则化更差。

        因此，[13] 通过提出一种组合了块稀疏和元素一般的稀疏（element-wise sparse）正则化的方法来改进块稀疏模型。他们将任务参数矩阵 $A$ 分解为两个矩阵 $B$ 和 $S$，其中 $A=B+S$。然后使用 $L_1/L_{\infty }$ 正则化强制 $B$ 为块稀疏，而使用 lasso 使 $S$ 成为元素一般的稀疏。最近，[14] 提出了组合稀疏正则化的分布式版本。

5.2 学习任务的关系

        尽管组合稀疏约束迫使我们的模型仅考虑几个特征，但这些特征大部分用于所有任务。所有之前的方法都基于假设：多任务学习的任务是紧密相关的。但是，不可能每个任务都与所有任务紧密相关。在这些情况下，与无关任务共享信息可能会伤害模型的性能，这种现象称为 负迁移（negative transfer）。

        与稀疏性不同，我们希望利用先验信息，指出相关任务和不相关任务。在这种情况下，一个能迫使任务聚类的约束可能更适合。[15] 建议通过惩罚任务列向量 $a_{.,1}，...，a_{.,t}$ 的范数与它们具有以下约束形式的方差来强加聚类约束：

$$\Omega =\Vert \bar{a}{\Vert }^2+\frac{\lambda }{T}\sum _{t=1}^T{\Vert a_{\cdot ,t}-\bar{a}\Vert }^2$$
其中
$$\bar{a}=\sum _{t=1}^T{a}_{\cdot ,t}/T$$

        为参数向量的均值。这个惩罚项强制将任务参数向量 $a_{.,1}，...，a_{.,t}$ 向由 λ 控制的均值聚类。他们将此约束应用于核函数方法，但这同样适用于线性模型。

        [16] 也提出了对于 SVM 的类似约束。这个约束受到贝叶斯方法的启发，并试图使所有模型接近平均模型。由于损失函数的平衡制约，使每个 SVM 模型的间隔（margin）扩大并产生类似于平均模型的结果。

        [17]在聚类的数量 $C$ 已知的假设下，通过形式化对 $A$ 的约束，使聚类正则化更加明确。然后他们将惩罚项分解为 3 个独立的范数：

• 衡量列参数向量平均大小的全局惩罚项：
  $${\Omega }_{mean}(A)=\Vert \bar{a}{\Vert }^2$$

• 衡量类间距离的类间方差（between-cluster variance）：
  $${\Omega }_{between}(A)=\sum _{c1}^C{T}_c{\Vert {\bar{a}}_c-\bar{a}\Vert }^2$$

        其中$T_c$是第 $c$ 个类中任务的数量，${\bar{a}}_c$是第 $c$ 个类中任务参数向量的均值向量。

• 衡量类内数据紧密度的类内方差（within-cluster variance）：
  $${\Omega }_{within}(A)=\sum _{c1}^C\sum _{t\in J(c)}{\Vert a_{\cdot ,t}-\bar{a}\Vert }^2$$

        其中 $J(c)$ 是第 $c$ 个类中任务的集合。

        最终的约束形式是这 3 个范数的加权和：

$$\Omega (A)={\lambda }_1{\Omega }_{mean}(A)+{\lambda }_2{\Omega }_{between}(A)+{\lambda }_3{\Omega }_{within}(A)$$

        由于此约束假设聚类是已知的，所以它们引入了上述惩罚项的凸松弛（convex relaxation），这使算法允许同时学习聚类。

        在另一种情况下，任务可能不在类结构中，但具有其它的结构。[18] 使用扩展组合 lasso 来处理树型结构（tree structure）中的任务，而 [19] 将其应用于具有图结构（graph structure）的任务。

        虽然之前对任务之间关系建模的方法使用了范数正则化，但也存在没有用到正则化的方法：[20] 第一个提出了使用 k-nn 的任务聚类算法，而 [21] 通过半监督学习从多个相关任务中学习通用结构。

        其它 MTL 任务之间关系的建模使用了贝叶斯方法：

• [22] 提出了使用模型参数先验的贝叶斯神经网络方法，来鼓励任务间使用相似的参数。[23] 将高斯过程（Gaussian process/GP）应用于 MTL，该方法利用 GP 推断共享协方差矩阵的参数。由于这在计算上非常昂贵，它们采用稀疏近似方案用来贪心地选择信息量最大的样本。[24] 同样将 GP 应用于 MTL，该方法利用 GP 假设所有模型抽样于同一个普通先验分布。
• [25] 在每个任务特定的层上使用高斯分布作为先验分布。为了鼓励不同任务之间的相似性，他们建议使用任务依赖的平均值，并引入使用混合分布的任务聚类。重要的是，它们首先需要确定聚类和混合分布数量的任务特征。

        基于此，[26] 使用 Dirichlet process 提取分布，并使模型能够学习任务之间的相似性以及聚类的数量。然后，算法在同一个类中的所有任务间共享相同的模型。[27] 提出了一个分层贝叶斯模型，它学习一个潜在的任务层次结构，而 [28] 对于 MTL 使用基于 GP 的正则化，并扩展以前的基于 GP 的方法，以便在更复杂的设置中增加计算的可行性。

        其它方法侧重于 on-line 多任务学习设置：[29] 将一些现有的方法，如 Evgeniou 等人的方法（2005）应用到 on-line 算法。他们还提出了一种使用正则化感知机（perceptron）的 MTL 扩展方法，该算法计算任务相关性矩阵。他们使用不同形式的正则化来偏置该任务相关性矩阵，例如，任务特征向量（characteristic vector）的接近程度或跨度子空间（spanned subspace）的维数。重要的是，与之前的方法类似，它们需要首先确定构成该矩阵的任务特征。[30] 通过学习任务关系矩阵来扩展之前的方法。

        [31] 假设任务形成相互分隔的组，并且每个组中的任务位于低维子空间中。在每个组内，任务共享相同的特征表征，其参数与组分配矩阵（assignment matrix）一起使用代替的最小化方案学习。然而，组之间的完全分隔可能不是理想的方式，因为任务可能分享一些有助于预测的特征。

        [32] 通过假设存在少量潜在的基础任务，反过来允许来自不同组的两个任务重叠。然后，他们将每个实际任务 $t$ 的参数向量 $a_t$ 建模为下面的线性组合：$a_t=L{s}_t$，其中 $L\in R^{k\times d}$ 是包含 $k$ 个潜在任务的参数向量的矩阵，而 $s_t\in R^k$ 是包含线性组合系数的向量。此外，它们约束潜在任务中的线性组合为稀疏；约束在稀疏模式下两个任务之间的重叠然后控制它们之间的共享数量。最后，[33] 学习一个小的共享假设池，然后将每个任务映射到一个假设。

6 深度神经网络的多任务学习的最新进展

        尽管最近的许多深度学习的工作都或显式或隐式使用了多任务学习作为其模型的一部分，但是使用方式仍然没有超出我们前面提到的两种方式：参数的硬共享与软共享。相比之下，仅有少部分的工作专注于提出深度神经网络中好的多任务学习机制。

6.1 深度关系网络（Deep Relationship Networks）

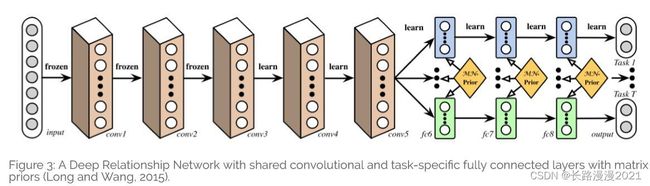
        在用于机器视觉的多任务场景中，已有的这些方法通常共享卷积层，将全链接层视为任务相关的。文献[34]提出了深度关系网络。除了共享层与任务相关层的结构，他们对全连接层添加矩阵先验。这将允许模型学习任务间的关系。这一点与我们之前看过的贝叶斯方法是类似的。然而，问题是这个方法依然依赖于事先预定义的共享结构。这一点对于机器视觉问题已经足够，但是对于新任务有错误倾向。

6.2 完全自适应特征共享（Fully-Adaptive Feature Sharing）

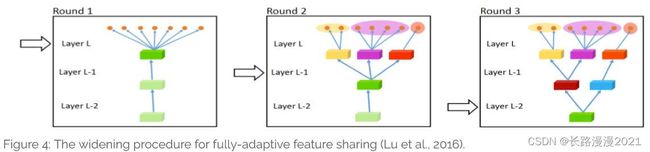
        从另一个极端说起，文献[35]提出了一个自底向上的方法。从瘦网络（thin network）开始，使用对相似任务自动分组的指标，贪心的动态加宽网络。这个加宽的过程动态创建分支，如下图所示。然而这种贪心的做法并不能得到全局的最优。为每个分支分配精确的一个任务，并不能允许模型学到更复杂的任务间的交互。

6.3 十字绣网络（Cross-Stitch Networks）

        文献[36]将两个独立的网络用参数的软共享方式连接起来。接着，他们描述了如何使用所谓的十字绣单元来决定怎么将这些任务相关的网络利用其他任务中学到的知识，并与前面层的输出进行线性组合。这种结构如下图所示，仅在pooling(池化)层与全连接层之后加入十字绣单元。

6.4 低层次监督（Low Supervision）

        相形之下，自然语言处理领域中近年来的多任务学习的工作重点在于找到一个好的层次结构：文献[37]展示了一些NLP中的基本工作，如词性标注，命名实体识别等，应该被作为辅助任务，在较低层次时进行有监督学习。

6.5 联合多任务模型（A Joint Many-Task Model）

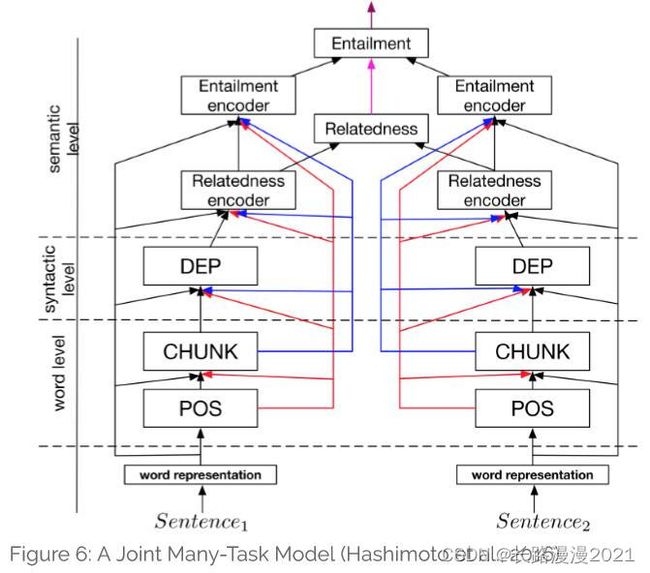
        基于这种发现，文献[38]预先定义了一个包含多个NLP任务的层次结构，如下图所示，并用来做多任务学习的联合模型。

6.6 用不确定性对损失进行加权（Weighting losses with Uncertainty）

        除了学习结构的共享，文献[39]采用一种正交的方法来考虑每个任务的不确定性。他们调整每个任务在代价函数中的相对权重，基于最大化任务相关的不确定性似然函数原理，来得到多任务学习的目标。对每个像素深度回归、语义分割、实例分割等三个任务的框架如下图所示。

6.7 多任务学习中的张量分解（Tensor factorisation for MTL ）

        近来许多工作试图将已有的多任务学习模型推广到深度学习中：文献[40]将已有的一些使用张量分解技术推广到模型参数划分来分解出每层的共享参数于任务的相关系数。

6.8 水闸网络（Sluice Networks）

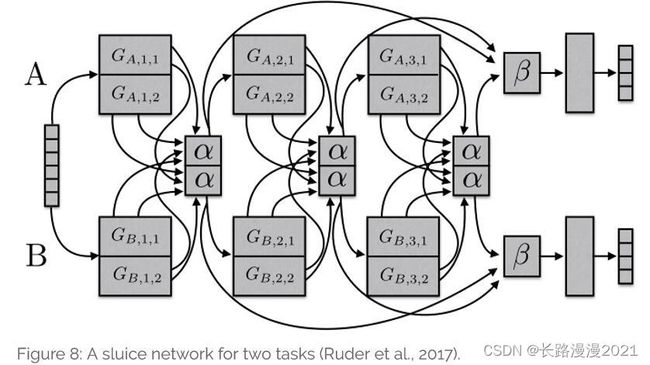
        最后我们说一下文献[41]中提到的水闸网络，它是对多种基于深度神经网络的多任务学习方法的泛化。如下图所示，这个模型可以学习到每层中哪些子空间是必须共享的，以及哪些是用来学习到输入序列的一个好的表示的。

6.9 参数共享+门控——MOE & MMOE模型

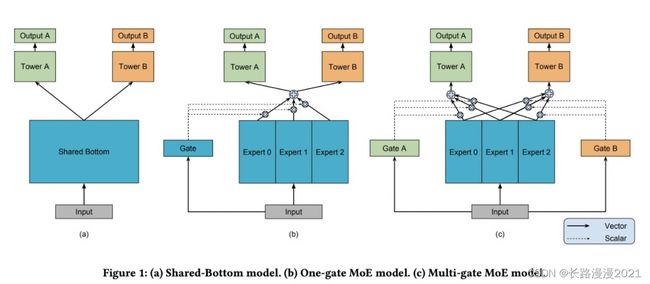
        相关性差的任务之间进行参数共享会产生跷跷板现象，为了解决这个问题，2017年Google第一次提出了MoE模型结构：OUTRAGEOUSLY LARGE NEURAL NETWORKS: THE SPARSELY-GATED MIXTURE-OF-EXPERTS LAYER（2017）。模型包括一个门控网络，输入样本特征，输出对每个Expert的选择得分，并将原来每层所有样本共享的参数，变成多组参数，每组参数被称为一个Expert。这篇工作最开始提出并不是为了解决多任务学习问题，而是实现了一种理论模型：在保证运算效率不大幅提升的前提下，通过多组参数增加模型容量，每个样本激活模型中的一部分参数。

        在此基础上，Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts（KDD 2018）提出了用多专家网络（MMoE）解决多任务学习问题。网络由多个多任务共享的Expert，以及每个任务独有的Gate网络构成。每一个任务$k$的具体输出结果表示如下（$f_i$表示第$i$个专家，$g^k$表示第$k$个任务的门网络）：
$$\begin{array}{c}{y}_k=h^k\left(f^k(x)\right)\\ \text{ where }{f}^k(x)=\sum _{i=1}^n{g}^k(x{)}_i{f}_i(x)\\ g^k(x)=\mathrm{softmax}\left(W_{gk}x\right)\end{array}$$

        通过这种方式，每个Task的门网络可以基于样本信息学习如何选择一组专家进行预测。MMoE通过这种灵活的模型设计，希望模型能够自动根据底层Task的关系学习Expert参数如何分配。例如，当底层任务关系较弱时，模型能够学到让每个Task只激活一个其对应的Expert，相当于将Experts分割给不同的任务。

        原论文的实验有个结论，在相同参数规模下要比share-bottom有明显的提升，对于相关性低的任务联合训练MMoE效果更加明显。

        然而，MMoE由于所有参数都是所有任务共享的，没有显示定义不同任务的私有参数，当不同任务的关系较弱时，可能会导致不同任务的跷跷板现象，即两个任务无法同时达到最好，一个任务效果提升，伴随着另一个任务效果下降。

6.10 CGC & PLE

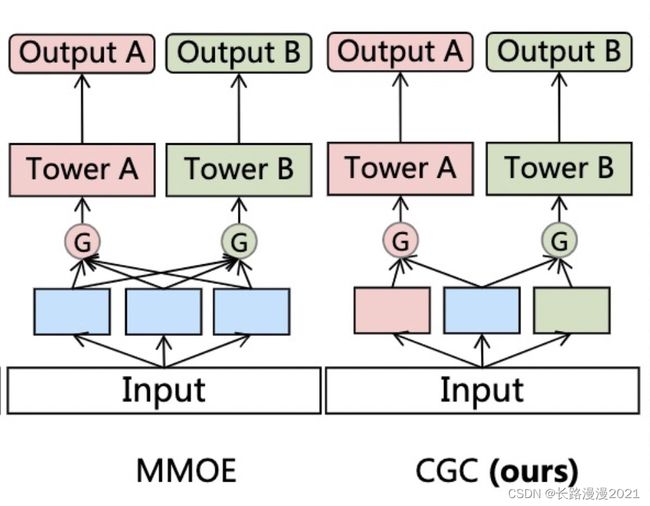
        可以看出CGC（PLE的简单版本）与MMOE主要区别在于，CGC模型中每个任务同时有共享的专家和独有的专家，而MMOE全部是共有的专家，作者认为这样可以拟合任务间复杂的相关性。

        相近的任务共享参数可以提高性能，不相近的任务会引入噪声降低性能，同时有共享参数和独有参数可以缓解这种噪声，即缓解跷跷板现象

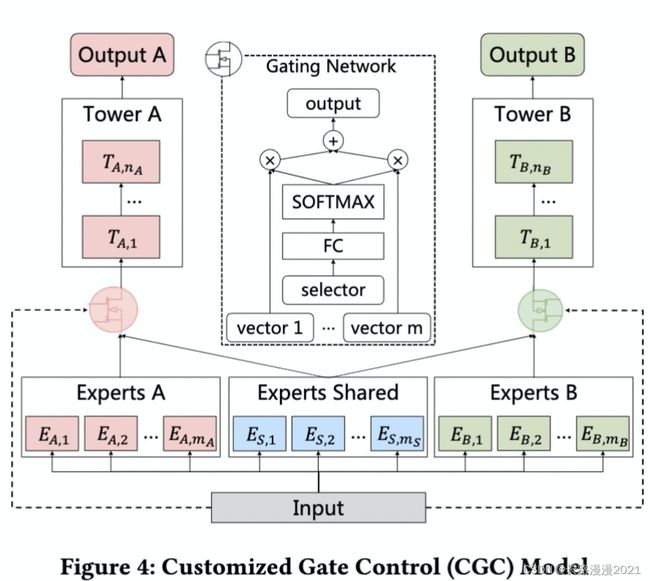
        CGC可以看作是Customized Sharing和MMoE的结合版本。每个任务有共享的Expert和独有的Expert。对任务A来说，将Experts A里面的多个Expert的输出以及Experts Shared里面的多个Expert的输出，通过类似于MMoE的门控机制之后输入到任务A的上层网络中。

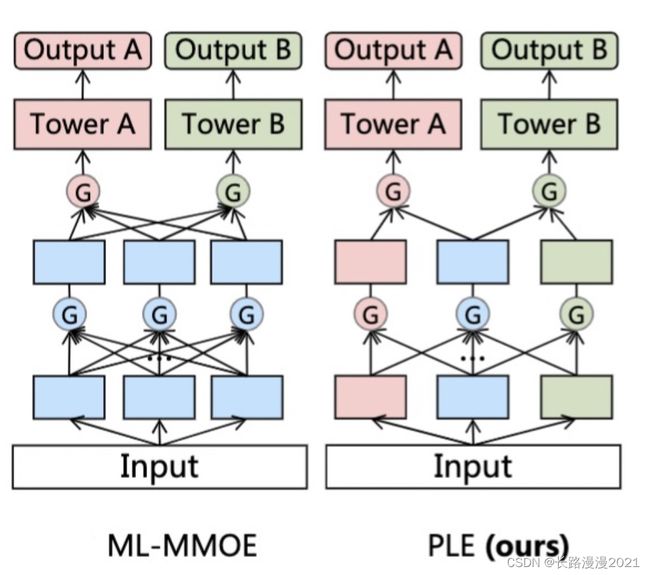
        在CGC的基础上，PLE考虑了不同的Expert之间的交互，可以看作是Customized Sharing和ML-MMOE的结合版本。Progressive Layered Extraction (PLE): A Novel Multi-Task Learning (MTL) Model for Personalized Recommendations（Recsys 2020）提出了PLE方法，将模型参数显示的划分为私有部分和公共部分，提升多任务学习的鲁棒性，缓解私有知识和公共知识之间的负向影响。PLE和MMoE的主要区别在于，将多专家分成公共部分和每个Task独有的部分。同时，论文中指出在网络最初阶段并不能真正确定哪些Expert需要共用哪些Expert独有。因此论文提出了多层次的信息提取方法，在网络的最底层增加多个Extraction Layer全局Gate，用来给所有Expert打分，在上层再区分公共和独有部分。其实可以理解底层先通过MoE不区分公共/私有部分提取基础特征，在上层再逐渐将公共/私有部分区分开。

        与CGC不同的是考虑了不同expert的交互性，在底层的Extraction网络中有一个share gate，他的输入不再是cgc的独有expert和share expert，而是全部expert .

        CGC/PLE作为MMOE/ML-MMOE的升级版，效果要好于MMOE/ML-MMOE

6.11 ESMM

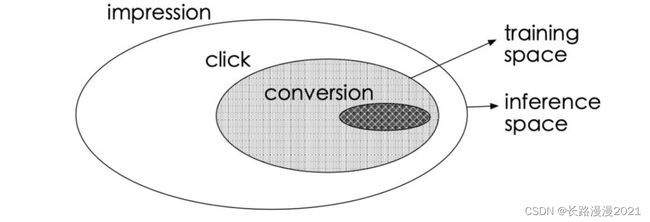
        ESMM是为了解决CVR预估面临的数据稀疏(DS)以及样本选择偏差(SSB)的问题。具体来说样本选择偏差指的是传统cvr用的是点击样本空间做训练集，但是使用时是针对全样本空间。数据稀疏指的是CVR训练数据的点击样本空间(click -> convertion)远小于CTR预估训练使用的曝光样本（show ->click）。

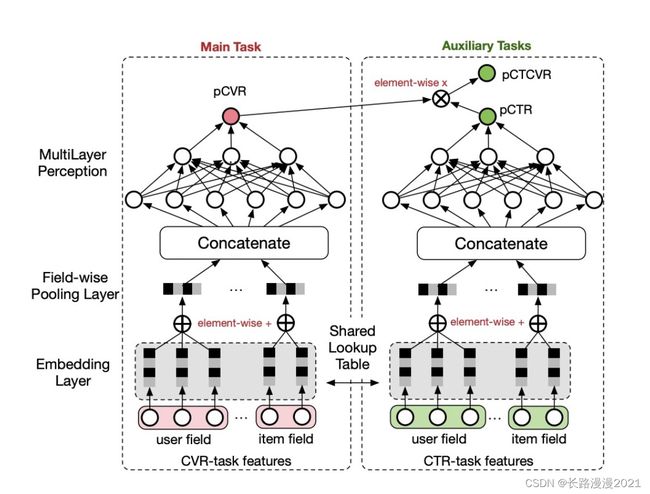
        ESMM 将 pCVR 作为一个中间变量，并将其乘以 pCTR 得到 pCTCVR，而不是直接基于有偏的点击样本子集进行 CVR 模型训练。pCTCVR 和 pCTR 是在全空间中以所有展现样本估计的，因此衍生的 pCVR 也适用于全空间并且缓解了 问题。此外，CVR 任务的特征表示网络与 CTR 任务共享，后者用更丰富的样本进行训练。这种参数共享遵循特征表示迁移学习范式，并为缓解 问题提供了显著的帮助。

$$\begin{array}{c}{p}_{CTR}=p(y=1\mid x)\\ p_{CTCVR}=p(y=1,z=1\mid x)\\ p_{CVR}=\frac{p_{CTCVR}}{p_{CTR}}\end{array}$$

        ESMM的损失函数如下，它由 CTR 和 CTCVR 任务中的两个损失项组成，这些任务通过所有展现次数的样本进行计算。
$$L\left({\theta }_{cvr},{\theta }_{ctr}\right)=\sum _{i=1}^{N}l\left(y_i,f\left(x_i,{\theta }_{ctr}\right)\right)+\sum _{i=1}^{N}l\left(z_i\&y_i,f\left(x_i,{\theta }_{ctr}\right)\cdot f\left(x_i,{\theta }_{cvr}\right)\right)$$

6.12 我的模型中应该共享些什么？

        已经回顾了这些相关工作，现在我们来总结一下在深度多任务学习模型中到底应该共享些什么信息。大多数的多任务学习中，任务都是来自于同一个分布的。尽管这种场景对于共享是有益的，但并不总能成立。为了研发更健壮的多任务模型，我们必须处理那些不相关的任务。

        早期用于深度学习的多任务模型需要预定义任务间的共享结构。这种策略不适合扩展，严重依赖于多任务的结构。早在1997年就已经提出的参数的硬共享技术在20年后的今天仍旧是主流。尽管参数的硬共享机制在许多场景中有用，但是若任务间的联系不那么紧密，或需要多层次的推理，则硬共享技术很快失效。最近也有一些工作研究学习哪些可以共享，这些工作的性能从一般意义上将优于硬共享机制。此外，若模型已知，学习一个任务层次结构的容量也是有用的，尤其是在有多粒度的场景中。

        正如刚开始提到的，一旦我们要做一个多目标的优化问题，那么我们就是在做多任务学习。多任务不应仅仅局限于将所有任务的知识都局限于表示为同一个参数空间，而是更加关注于如何使我们的模型学习到任务间本应该的交互模式（it is thus helpful to draw on the advances in MTL that we have discussed and enable our model to learn how the tasks should interact with each other）。

---

7 辅助任务（Auxiliary Tasks）

        对于同时获得多个任务的预测结果的场景，多任务学习是天然适合的。这个场景在金融或经济的预测中是常见的，比如，我们可能既想知道相关的影响因子，又想知道预测结果。在生物信息学中，我们可能想同时知道多种疾病的症候。但是在大多数情况下，我们仅关注一个任务。本节中，我们将讨论如何找到一个辅助任务来使得多任务学习受益。

7.1 相关任务（Related Tasks）

        使用相关任务作为一个辅助任务，对于多任务学习来说，是一个典型的选择。想要知道什么是“相关任务”，此处我们展示一些直观的例子。Caruana于1997年使用预测不同道路的特征来辅助学习自动驾驶的方向掌控。文献[42]使用头部姿势估计与面部特征属性推断辅助脸部轮廓检测任务。文献[43]同时学习查询分类与网页搜索。文献[44]同时预测图像中物体的类别和位置。文献[45]同时预测文本到语言的过程中音素的持续时间和频率。

7.2 对抗性（Adversarial）任务

        通常情况下，对于一个相关任务来说，不存在标注数据。然而，在一些场合，我们可以用的任务与我们想要实现的目标是相反的。这样的数据是可以用来做对抗损失的。这些损失不是用来做最小化的，而是使用Gradient Reversal Layer来做最大化训练误差的。文献[46]中展示了这种场景在领域自适应方面的成功例子。这种场景中的对抗任务用来预测输入的领域。通过对对抗任务的梯度求逆，对抗任务损失最大化。这样对于主任务是有利的，可以促使模型学习到不用区分两个域的表示。

7.3 提示（Hints）性任务

        如前所述，多任务学习可以学到单任务学不到的特征。使用Hints就是这样一种有效的机制：在辅助任务中预测特征。最近的一个例子是在自然语言处理中，文献[47]在情感分析中将一个输入句子中是否包含正负面情感词作为辅助任务。文献[48]在错误名字识别中将判断一个句子中是否包含名字作为辅助任务。

7.4 注意力集中

        辅助任务可以用来将注意力集中在网络可能忽略的图像的某部分上。例如，对于学习方向掌控的任务中，单一的任务模型通常忽略那些图像的细微之处，如路标等。那么预测路标就可以作为一个辅助任务。迫使模型学会去表示它们，这样的知识可以用于主任务。类似的，对于脸部识别来说，既然这些脸是不同的，我们就可以将预测脸部特征的位置作为辅助任务。

7.5 量化平滑

        对于多任务来讲，优化目标是已经被量化的。通常连续型的是受欢迎的，而可用的标注是离散集合。在大多数情况下，需要人工评价来收集数据，例如，预测疾病的风险或情感分析（正面、负面、中立），由于目标函数是光滑的，所以使用较少量的量化辅助任务会使学习变得容易。

7.6 预测输入

        在一些情况下使用某些特征作为输入并不会对预测目标输出有益。然而，它们可能能指导监督学习的过程。在这些情形下，特征是作为输出的一部分，而非输入。文献[49]展示了这些问题在实际应用中的场景。

7.7 用未来预测现在

        许多场景中一些特征仅在做出预测后才可用。例如，在自动驾驶中，一旦汽车经过障碍物或路标，便可以对它们做出准确的度量。Caruana于1997年举了一个肺炎的例子，只有事发后才能又额外的诊断案例可用。对于这些例子来讲，这些额外的数据由于在输入的时刻并不可用，所以并不能作为特征。然而，可以用作辅助任务来为模型传授额外的知识以辅助训练。

7.8 表示学习

        多任务学习中辅助任务的目标在于使得模型学习到共享的表示，以帮助主任务的学习。我们目前所讨论到的辅助任务都是隐式的在做这件事情。由于它们和主任务密切相关，所以在学习的同时可能允许这些模型学到有利于主任务的表示。一个更为显式的做法是利用一个辅助任务专门来学习一个可以迁移的表示。Cheng等人2015年的一个工作以及文献[50]所采用的语言模型目标就起到了这样的作用。类似的，autoencoder也是可以用来做辅助任务的。

---

8 为什么辅助任务对主任务是有益的？

        虽然在实际当中我们可能仅仅关心一种辅助任务，但是前面我们已经讨论了在多任务学习中可能用的各种辅助任务。尽管我们并不知道在实际中哪种会起作用。寻找辅助任务的一个基本假设是：辅助任务应该是与主任务密切相关的，或者是能够对主任务的学习过程有益的。

        然而，我们并不知道什么样的两个任务是相关的或相似的。Caruana在1997年给出的定义是：若两个任务使用相同的特征来做决策，那么两个任务是相似的。Baxer于2000年补充道：理论上讲相关的任务共享同一个最优的假设类，也就是同样的归纳偏置（inductive bias）。文献[51]提出若两个任务中的数据都产生自由同一类变换F得到固定的概率分布，那么两个任务是F相关的。尽管可以使用于同一个分类问题，但是不能用于处理不同问题的任务。Xue等人2007年提出若两个任务的分类边界（参数向量）是闭合的，那么两个任务是相似的。

        虽然早期在理解任务相关性的理论定义方面取得了一些进展，但是近期的成果却没有。任务相似性不是二值的，而是一个范围。更相似的两个任务在多任务学习中受益更大，而反之亦然。使得我们的模型能够学习到共享哪些参数可能只是暂时克服了理论上的缺失，以及更好的利用联系不紧密的任务。然而，我们也很需要对任务相似性的理论认知，来帮助我们了解如何选择辅助任务。

        文献[52]发现具有完备且统一的标注分布的辅助任务对于序列标注主任务应该更有益，这一点在实验中已经得到验证。此外，文献[53]发现non-plateauing的辅助任务也会为plateauing的主任务带来改善。

        然而这些实验都是具有范围局限性的。近期的这些研究成果只是为我们进一步理解神经网络中的多任务学习提供了一些线索。

---

9 结论

9.1 多任务学习与其他学习算法之间的关系

        多任务学习（Multitask learning）是迁移学习算法的一种，迁移学习之前介绍过。定义一个一个源领域source domain和一个目标领域（target domain），在source domain学习，并把学习到的知识迁移到target domain，提升target domain的学习效果（performance）。

        多标签学习（Multilabel learning）是多任务学习中的一种，建模多个label之间的相关性，同时对多个label进行建模，多个类别之间共享相同的数据/特征。

        多类别学习（Multiclass learning）是多标签学习任务中的一种，对多个相互独立的类别（classes）进行建模。这几个学习之间的关系如下图所示：

9.2 多任务学习在实际使用的时候有什么技巧和注意事项

        想强调一下，在一头扎入多任务模型共享参数改进、loss设计的时候不要忘记了深度学习/机器学习最纯真的东西：

        数据！洗掉你的脏数据！

        NLP领域大家都专注于几个数据集，很大程度上这个问题比较小，但推荐系统的同学们，这个问题就更常见了。

        静下心来理解你的数据、特征的含义、监督信号是不是对的，是不是符合物理含义的（比如你去预测视频点击，结果你的APP有自动播放，自动播放算点击吗？播放多久算点击？）。

        对于想快速提升效果的同学，也可以关注以下几点：

• 如果MTL中有个别任务数据十分稀疏，可以直接尝试一下何凯明大神的Focal loss！笔者在短视频推荐方向尝试过这个loss，对于点赞/分享/转发这种特别稀疏的信号，加上它说不定你会啪一下站起来的。
• 仔细分析和观察数据分布，如果某个任务数据不稀疏，但负例特别多，或者简单负例特别多，对负例进行降权/找更难的负例也可能有奇效果哦。正所谓：负例为王。
• 另外一个其实算trick吧？将任务A的预测作为任务B的输入。实现的时候需要注意：任务B的梯度别再直接传给A的预测了。

        最后的最后是：读一读机器学习/深度学习训练技巧，MTL终归是机器学习，不会逃离机器学习的范围的。该搜的超参数也得搜，Dropout，BN都得上。

        无论是MTL，还是single task先把baseline做高了做对了，走在正确的道路上，你设计的模型、改正的loss，才有置信的效果～～。

        本文关注了多任务学习的历史以及在深度神经网络中多任务学习的最新进展。尽管多任务学习频繁使用，但是近20年的参数硬共享机制仍旧是神经网络中多任务学习的主要范式。学习共享哪些信息的工作看起来更具前景。同时，我们对于任务的相似性，任务间的关系，任务的层次，以及多任务学习的收益等的理解仍旧是有限的，我们需要学习更多以理解深度神经网络中多任务学习的泛化能力。

---

10 参考文献

[1] Caruana. R. (1998). Multitask Learning. Autonomous Agents and Multi-Agent Systems. 27(1). 95-133.
[2] Caruana. R. Multitask Learning: A Knowledge based Source of Inductive Bias. Proceedings of the Tenth International Conference on Machine Learning. 1993.
[3] Baxter, J. (1997) A Bayesian / Information Theoretic Model of Learning to Learn via Multiple Task Sampling. Machine Learning. 28, 7-39.
[4] Duong, L., Cohn. et.al. 2015. Low Resource Dependency Parsing Cross-Lingual Parameter Sharing in a Neural Network Parser. ACL2015.
[5] Yang, Y. et. al. 2017. Trace Norm Regularized Deep Multi-Task Learning. ICLR2017 workshop.
[6] Abu-Mostafa, et. al. 1990. Learning from Hints in Neural Networks, Journal of Complexity.
[7] Baxter, J. 2000. A Model of Inductive Bias Learning. Journal of Aritificial Intelligence Research.
[8] Argyriou, A. 2007. Multi-Task Feature Learning. NIPS2007.
[9] C. Zhang and J. Huang. 2008. Model Selection Consistency of the Lasso Selection in High Dimensional Linear Regression. Annals of Statistics. 2008.
[10] Yuan, Ming and Yi Lin. 2006. Model Selection and Estimation in Regression with Grouped Variables. Journal of the Royal Statistical Society. 2006.
[11] Lounici. K, et.al. 2009. Taking Advantage of Sparsity in Multi-task Learning. stat.2009.
[12] Negahban, S. et. al. 2008. Joint Support Recovery under High Dimensional Scaling: Benefits and Perils of L1,\inf-regularization. NIPS2008.
[13] Jalali, A. et.al. 2010. A Dirty Model for Multi-Task Learning. NIPS2010.
[14] Liu, S. et.al. 2016. Distributed Multi-Task Relationship Learning. AISTATS2016.
[15] Evgeniou, T. et. al. 2005. Learning Multiple Tasks with Kernel Methods. Journal of Machine Learning Research 2005.
[16] Evgeniou, T. et. al. 2004. Regularized Multi-Task Learning. KDD2004.
[17] Jacob, L. et. al. 2009. Clustered Multi-Task Learning: A Convex Formulation . NIPS2009.
[18] Kim, S. and Xing, Eric P. 2010. Tree-Guided Group Lasso for Multi-Task Regression with Structured Sparsity. ICML2010.
[19] Chen, X. et. al. 2010. Graph Structured Multi-Task Regression and An Efficient Optimization Method for General Fused Lasso.
[20] Thrun, S. et. al.1996. Discovering Structure in Multiple Learning Tasks: The TC Algorithm. ICML1998.
[21] Ando, R, K. et. al. 2005. A Framework for Learning Predictive Structures from Multiple Tasks and Unlabeled Data. JMLR2005.
[22] Heskes, T. 2000. Empirical Bayes for Learning to Learn. ICML2000.
[23] Lawrence, N.D. et. al. 2004. Learning to Learn with the informative vector machine. ICML2004.
[24] Yu, K. et. al. 2005. Learning Gaussian Processes from Multiple Tasks, ICML2005.
[25] Bakker, B. et. al. 2003. Task Clustering and Gating for Bayesian Multi-Task Learning. JMLR2003.
[26] Xue, Y. et. al. 2007. Multi-Task Learning for Classification with Dirichlet Process Priors. JMLR2007.
[27] Daume III, H. et. al. 2009. Bayesian Multitask Learning with Latent Hierarcies.
[28] Zhang, Y. et.al. 2010. A Convex Formulation for Learning Task Relationships in Multi-Task Learning. UAI2010.
[29] Cavallanti, G. et. al. 2010. Linear Algorithms for Online Multitask Classification. JMLR2010.
[30] Saha, A. et. al. 2011. Online Learning of Multiple Tasks and their Relationships. JMLR2011.
[31] Kang, Z. et. al. 2011. Learning with Whom to Share in Multi-task Feature Learning. ICML2011.
[32] Kumar, A. et. al. 2012. Learning Task Grouping and Overlap in Multi-Task Learning. ICML2012.
[33] Crammer, K. et. al. 2012. Learning Multiple Tasks Using Shared Hypotheses. NIPS2012.
[34] Long, M. et. al. 2015. Learning Multiple Tasks with Deep Relationship Networks.
[35] Lu, Y. et. al. 2016. Fully-Adaptive Feature Sharing in Multi-Task Networks with Applications in Person Attriute Classification.
[36] Misra, I. et. al. Cross-Stitch Networks for Multi-Task Learning, CVPR2016.
[37] Sogaard, A. et. al. Deep Multi-Task Learning with Low Level Tasks Supervised at Lower Layers. ACL2016.
[38] Hashimoto , K. 2016. A Joint Multi-Task Model: Growing A Neural Network for Multiple NLP Tasks.
[39] Kendail, A. et. al. 2017. Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics.
[40] Yang, Y. et. al. 2017. Deep Multi-Task Representation Learning: A Tensor Factorization Approach. ICLR2017.
[41] Ruder, S. 2017. Sluice Networks: Learning What to Share between Loosely Related Tasks.
[42] Zhang, Z. 2014. Facial Landmark Detection by Deep Multi-Task Learning. ECCV2014.
[43] Liu, X. et. al. 2015. Representation Learning Using Multi-Task Deep Neural Networks for Semantic Classification and Information Retrieval.
[44] Girshick, R. 2015. Fast R-CNN. ICCV2015.
[45] Arik, S. O. et. al. 2017. Deep Voice: Real-time Neural Text-to-Speech. ICML2017.
[46] Ganin, T. 2015. Unsupervised Domain Adaptation by Backpropagation. ICML2015.
[47] Yu, J. 2016. Learning Sentence Embeddings with Auxiliary Tasks for Cross Domain Sentiment Classification. EMNLP 2016.
[48] Cheng, H. 2015. Open-Domain Name Error Detection Using a Multi-Task RNN. EMNLP2015.
[49] Caruana, R. et. al. 1997. Promoting Poor Features to Supervisors: Some Inputs work Better as outputs. NIPS1997.
[50] Rei, M. 2017. Semi-supervised Multitask Learning for Sequence Labeling, ACL2017.
[51] Ben-David, S. et. al. 2003. Exploiting Task Relatedness for Multiple Task Learning. Learning Theory and Kernel Machines.
[52] Alonso, H. M. et. al. 2017. When is Multi-Task Learning Effective? Multitask Learning for Semantic Sequence Prediction Under Varying Data Conditions. EACL2017.
[53] Bingel, J. et. al. 2017. Identifying Beneficial Task Relations for Multi-Task Learning in Deep Neural Networks, EACL2017.

---

        这部分主要来自机器之心的一篇文章，一文读懂深度神经网络多任务学习

---

参考博文

• 共享相关任务表征，一文读懂深度神经网络多任务学习：https://mp.weixin.qq.com/s?__biz=MzA3MzI4MjgzMw==&mid=2650728311&idx=1&sn=62b2dcc82657d1ce3bf91fd6a1197699
• Multi-task Learning(Review)多任务学习概述：https://zhuanlan.zhihu.com/p/59413549
• 多任务学习-Multitask Learning概述：https://zhuanlan.zhihu.com/p/27421983
• 浅谈多任务学习（Multi-task Learning）：https://zhuanlan.zhihu.com/p/348873723
• 一文梳理多任务学习(MMoE/PLE/DUPN/ESSM等)：https://www.mdnice.com/writing/97259273dc1347c586be466995327c14
• 一文梳理多任务学习(MMoE/PLE/DUPN/ESSM等)：https://zhuanlan.zhihu.com/p/363059498