深入浅出了解GNN的几种变体

接上篇博客，这周主要学习了GraphSAGE，GAT，R-GCN 三种GNN的变体模型，从空域的角度出发，对节点的嵌入表征进行了深入的研究。（本文作为笔者的学习笔记，如有错误，希望各位读者批评指正） - - 更新时间:2020年11月8日

[学习笔记(1)]深入浅出了解GCN原理(公式+代码)
[学习笔记(2)]深入浅出了解GNN的几种变体

  再上一章的内容里，我们主要从频域的角度推导出了图卷积的一般表达式，通过简化最终得到了图卷积公式（1），从空域视角来看，其本质就是一个 迭代式地聚合邻居节点的过程，这种模型聚合的设计，大大加强了 大规模图数据的适应性。基于此思想的设计，一些GNN的变体框架也相继提出，这些框架从更加统一的层面，抽象出了GNN的表达式。本章我们简单介绍几种 GNN的变体，这些变体从空域卷积出发，对节点的embedding以及边关系的信息归纳有了更强大的表达能力。

$$H^{(l+1)}=\sigma ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)})（1）$$

GraphSAGE(SAmple and aggreGatE）

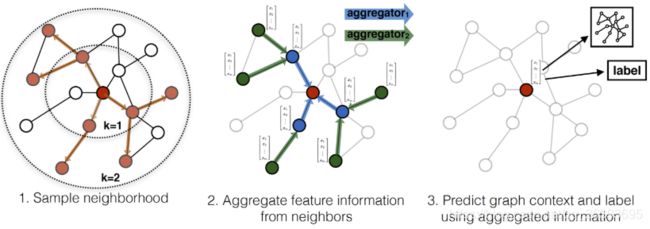
  GraphSAGE是基于之前图嵌入Transductive学习的一些缺点，提出的一个Inductive的算法，目前为止，大多数现有的使用图卷积网络生成节点嵌入的方法仅应用于具有固定图的转换，其本质上都是transductive.（直推式）的方式，对于每个节点的嵌入，使用全局的节点信息，每次迭代所有的训练样本贡献一次梯度，而无法做到min-batch的训练方式，这在很多实际大规模数据的应用场景下是无法实现的。同时这种方式，对于 "unseen"的节点 并不能很好的表示，每次增加新的节点，图结构就会发生变换，为了与新加入的节点对齐，得到修正后的embedding，需要重新训练整个新的数据集。基于以上几点的考虑，作者推出了GraphSAGE (SAmple and aggreGatE)，一种Inductive的方式对node嵌入学习。

聚合函数

  在GCN的模型中，节点在第K层的特征，只与其邻居K-1层的特征有关，这种局部特性，使得节点在每一层的特征，只与其K阶子图有关，运用在大规模的图数据中，我们就只需要考虑每个节点的K阶邻居即可，而不需要一次性训练全局的信息。

Fig1 GraphSAGE 采样与聚合方法可视化

  考虑现实世界中，数据节点的度往往呈指数级增长，这样会使得计算和存储代价变的不可控制，所以GraphSAGE采用有放回的均匀随机采样，从而固定选择邻接节点的数量，事实上我们还可以采用其他形式的分布，或者自适应的方式来选取邻接节点。

这里先直接附上论文中的算法步骤,算法的具体实施流程如下所示：
  Embedding generation (i.e., forward propagation) algorithm ，该流程描述了如何使用聚合函数对节点的邻居信息进行聚合，从而生成目标节点的embedding。

每一次的迭代，每层的源节点都会从它的局部邻居聚合信息，迭代次数越多，聚合节点的信息范围就越广。直接看上述流程可能还不是很清楚，接下来我会贴出代码和注释，并对算法流程中的聚合与连接操作进行讲解。

我们来看看聚合操作，GraphSAGE聚合节点的操作需要满足以下三点：

• 聚合操作后维度保存一致
• 聚合的节点需要具有排列不变性。我们了解的图像和序列数据，前者包含空间顺序，后者包含时序顺序，而图数据本身是无序的数据结构
• 聚合操作必须可导

论文中，作者主要提出了三种聚合方式：
由于原文中的公式我自认为写的不是很清楚，感兴趣的读者可以自行阅读原文 (Inductive Representation Learning on Large Graphs)。这里我根据代码中给出的计算方法，重新写了计算表达公式，将三种形式的聚合以及两种连接方式统一到了一个表达式：

$$Ag{g}^{sum}:h_v^K=\sigma (\{h_v^{K-1}\cdot {\theta }_1^{d\times m}\}\cup Aggregate\{h_u^{K-1},\forall u\in \mathcal{N}(v)\}\cdot {\theta }_2^{d\times m}).(2)$$
其中：

• 第K次迭代的源节点$h_v^K$ 的embedding由第k-1次迭代的节点$h_v^{K-1}$ 与其采样的邻居节点$h_u^{K-1}$聚合表示后的连接得到。
• 聚合$Aggregate$操作可分为MEAN,MAX和LSTM三种聚合方式
• $\cup$分为两种连接方式，一种是SUM 直接相加，另一种是CONCAT 特征维度上拼接，这种连接方式可以看作是不同搜索深度或GraphSAGE算法层之间的 Skip connection(跳跃连接) 的简单形式，它可以显著提高模型性能。
• $\sigma$是sigmoid函数，做非线性变换
• $\theta$是可学习的参数矩阵

简单补充说明下文中提到的三种Aggregate操作：
Mean aggregator.：
平均聚合算子，逐元素求和取平均，这种操作是GCN中图卷积传导的线性近似。
LSTM aggregator
LSTMs 的聚合器有加更强大的表达能力，但是，LSTMs不是symmetric的，不具有permutation invariant(排列不变性)，因为LSTM的输入是以序列的方式处理，具有时序性。因此，需要先对邻居节点顺序随机打乱，然后将邻居序列的embedding作为LSTM的输入。
Pooling aggregator
类似于图像中的池化操作，elementwise级别的 max-pooling操作来跨邻集聚合信息。

参数学习

基于图的有监督学习方式，这里就不过多说明，通过GraphSAGE得到的节点embedding，配合下游多个任务使用。监督学习的形式可根据任务的不同设置不同的目标函数即可，比如节点分类任务可使用交叉熵损失函数。

基于图的无监督学习方式，倾向于使得相邻的顶点有相似的表示，同时也会使相互远离的顶点的表示差异变大：
$$J_g(z_u)=-log(\sigma (z_u^T{z}_v))-Q\cdot {\mathbb{E}}_{v_n\sim P_n(v)}log(\sigma (-z_u^T{z}_{v_n}))(3)$$

• $v$是$u$通过定长随机游走可达的邻居，$Z_v,Z_u$是GraphSAGE得到的节点embedding
• $P_n(v)$是一个负采样分布
• $Q$定义为负采样个数

节点表示$z_u$是从包含在节点的本地邻居的特征中生成的，而不是为每个节点训练一个唯一的嵌入表示。节点之间的相似度，通过点积来表示。这个表达式作为无监督学习的方式，可为下游任务作为一个预训练的服务，在有监督学习中的任何一个损失函数都可以将其替换。

代码

代码部分主要参考GraphSage示例
  首先需要对邻居节点采样，我们维护一个节点及其邻居对应关系的表，比如{0:[2,4],1:[2,5]…} ，每个节点都列出其对应的邻居。我们通过sampling和multihop_sampling来实现批次的邻居节点采样操作。

def sampling(src_nodes, sample_num, neighbor_table):
    """根据源节点采样指定数量的邻居节点，注意使用的是有放回的采样；
    某个节点的邻居节点数量少于采样数量时，采样结果出现重复的节点
    
    Arguments:
        src_nodes {list, ndarray} -- 源节点列表
        sample_num {int} -- 需要采样的节点数
        neighbor_table {dict} -- 节点到其邻居节点的映射表
    
    Returns:
        np.ndarray -- 采样结果构成的列表
    """
    results = []
    for sid in src_nodes:
        # 从节点的邻居中进行有放回地进行采样
        res = np.random.choice(neighbor_table[sid], size=(sample_num, ))
        results.append(res)
    return np.asarray(results).flatten()


def multihop_sampling(src_nodes, sample_nums, neighbor_table):
    """根据源节点进行多阶采样
    
    Arguments:
        src_nodes {list, np.ndarray} -- 源节点id
        sample_nums {list of int} -- 每一阶需要采样的个数
        neighbor_table {dict} -- 节点到其邻居节点的映射
    
    Returns:
        [list of ndarray] -- 每一阶采样的结果
    """
    sampling_result = [src_nodes]
    for k, hopk_num in enumerate(sample_nums):
        hopk_result = sampling(sampling_result[k], hopk_num, neighbor_table)
        sampling_result.append(hopk_result)
    return sampling_result

其次是网络中的Aggregator的聚合操作，接收采样后的neighor_feature，shape=(batch_size，neighor_nums,feature_dim)，对其在第二个维度neighor_nums上聚合.

class NeighborAggregator(nn.Module):
    def __init__(self, input_dim, output_dim, 
                 use_bias=False, aggr_method="mean"):
        """聚合节点邻居

        Args:
            input_dim: 输入特征的维度
            output_dim: 输出特征的维度
            use_bias: 是否使用偏置 (default: {False})
            aggr_method: 邻居聚合方式 (default: {mean})
        """
        super(NeighborAggregator, self).__init__()
        self.input_dim = input_dim
        self.output_dim = output_dim
        self.use_bias = use_bias
        self.aggr_method = aggr_method
        self.weight = nn.Parameter(torch.Tensor(input_dim, output_dim))
        if self.use_bias:
            self.bias = nn.Parameter(torch.Tensor(self.output_dim))
        self.reset_parameters()
    
    def reset_parameters(self):
        init.kaiming_uniform_(self.weight)
        if self.use_bias:
            init.zeros_(self.bias)

    def forward(self, neighbor_feature):
        if self.aggr_method == "mean":
            aggr_neighbor = neighbor_feature.mean(dim=1) #聚合
        elif self.aggr_method == "sum":
            aggr_neighbor = neighbor_feature.sum(dim=1)
        elif self.aggr_method == "max":
            aggr_neighbor = neighbor_feature.max(dim=1)
        else:
            raise ValueError("Unknown aggr type, expected sum, max, or mean, but got {}"
                             .format(self.aggr_method))
        
        neighbor_hidden = torch.matmul(aggr_neighbor, self.weight)
        if self.use_bias:
            neighbor_hidden += self.bias

        return neighbor_hidden

    def extra_repr(self):
        return 'in_features={}, out_features={}, aggr_method={}'.format(
            self.input_dim, self.output_dim, self.aggr_method)

聚合后的数据，执行Skip connection的连接，如上文提到的sum或concatenate操作。

class SageGCN(nn.Module):
    def __init__(self, input_dim, hidden_dim,
                 activation=F.relu,
                 aggr_neighbor_method="mean",
                 aggr_hidden_method="sum"):
        """SageGCN层定义

        Args:
            input_dim: 输入特征的维度
            hidden_dim: 隐层特征的维度，
                当aggr_hidden_method=sum, 输出维度为hidden_dim
                当aggr_hidden_method=concat, 输出维度为hidden_dim*2
            activation: 激活函数
            aggr_neighbor_method: 邻居特征聚合方法，["mean", "sum", "max"]
            aggr_hidden_method: 节点特征的更新方法，["sum", "concat"]
        """
        super(SageGCN, self).__init__()
        assert aggr_neighbor_method in ["mean", "sum", "max"]
        assert aggr_hidden_method in ["sum", "concat"]
        self.input_dim = input_dim
        self.hidden_dim = hidden_dim
        self.aggr_neighbor_method = aggr_neighbor_method
        self.aggr_hidden_method = aggr_hidden_method
        self.activation = activation
        self.aggregator = NeighborAggregator(input_dim, hidden_dim,
                                             aggr_method=aggr_neighbor_method)
        self.weight = nn.Parameter(torch.Tensor(input_dim, hidden_dim))
        self.reset_parameters()
    
    def reset_parameters(self):
        init.kaiming_uniform_(self.weight)

    def forward(self, src_node_features, neighbor_node_features):
        neighbor_hidden = self.aggregator(neighbor_node_features)
        self_hidden = torch.matmul(src_node_features, self.weight)
        
        if self.aggr_hidden_method == "sum": # 两种连接方式
            hidden = self_hidden + neighbor_hidden
        elif self.aggr_hidden_method == "concat":
            hidden = torch.cat([self_hidden, neighbor_hidden], dim=1)
        else:
            raise ValueError("Expected sum or concat, got {}"
                             .format(self.aggr_hidden))
        if self.activation:
            return self.activation(hidden)
        else:
            return hidden

    def extra_repr(self):
        output_dim = self.hidden_dim if self.aggr_hidden_method == "sum" else self.hidden_dim * 2
        return 'in_features={}, out_features={}, aggr_hidden_method={}'.format(
            self.input_dim, output_dim, self.aggr_hidden_method)

设置好一层的SAG后，我们封装多层的GraphSage模型，这里默认参数设置的是两层，也可以设置多层，但文章中作者表示一般2层就能达到很好的效果了.

• num_neighbors_list=[10,10] # 每阶采样邻居的节点数设置为10
• num_layers=len(num_neighbors_list)=2，SAG卷积层数

class GraphSage(nn.Module):
    def __init__(self, input_dim, hidden_dim,
                 num_neighbors_list):
        super(GraphSage, self).__init__()
        self.input_dim = input_dim
        self.hidden_dim = hidden_dim
        self.num_neighbors_list = num_neighbors_list
        self.num_layers = len(num_neighbors_list)
        self.gcn = nn.ModuleList()
        self.gcn.append(SageGCN(input_dim, hidden_dim[0]))
        for index in range(0, len(hidden_dim) - 2):
            self.gcn.append(SageGCN(hidden_dim[index], hidden_dim[index+1]))
        self.gcn.append(SageGCN(hidden_dim[-2], hidden_dim[-1], activation=None))

    def forward(self, node_features_list):
        hidden = node_features_list# [[0],[1],[2]]
        for l in range(self.num_layers):#2
            next_hidden = []
            gcn = self.gcn[l]
            for hop in range(self.num_layers - l):
                src_node_features = hidden[hop]
                src_node_num = len(src_node_features)
                neighbor_node_features = hidden[hop + 1] \
                    .view((src_node_num, self.num_neighbors_list[hop], -1)) # 这里形状需要reshape下
                h = gcn(src_node_features, neighbor_node_features)
                next_hidden.append(h)
            hidden = next_hidden
        return hidden[0]

    def extra_repr(self):
        return 'in_features={}, num_neighbors_list={}'.format(
            self.input_dim, self.num_neighbors_list
        )

为了读者更好的理解，这里我举个例子来说明迭代部分的代码，以上述参数为例:

1、首先输入一个mini_batch数据，shape=(batch_size,k)

2、 对其进行邻接采样得到neighbors_feature，由于我们是两层的，所以采样两次,每个源节点得到10个邻居节点.[(batch_size,k),(batch_size * 10,k),(batch_size * 10*10,k)]

3、在迭代阶段，第K层节点由第K-1层的邻居节点聚合连接得到.
起始$hidden=[(batch,k_0{)}^{(0)},(batch\ast 10,k_0{)}^{(0)},(batch\ast 10\ast 100,k_0{)}^{(0)}]$
第一次迭代后：$hidden=[(batch,k_1{)}^{(1)},(batch\ast 10,k_1{)}^{(1)}]$
第二次迭代后:$hidden=[(batch,k_2{)}^{(2)}]$

于是我们就得到了batch节点经过两次迭代聚合后的embedding表达，embedding的维度为$k_2$。

总结

  GraphSAGE解决了小批量训练的问题，对于新加入的节点也能很好的适应并跟新，使得我们在大型的图结构数据中将模型落地成为可能，同时GraphSAGE更重要的作用是通过聚合邻居节点，对图节点进行有效的嵌入表示，为下游任务注入了先验知识。

GAT(Graph Attention Networks)

  介绍了上面Inductive的学习方式来对节点聚合，接下来介绍的是图注意力网络GAT(Graph Attention Networks),它通过注意力机制来对邻居节点聚合，实现了对邻居权重的自适应分配，这一机制与CV和NLP领域中多头的self-Attention是一致的，这也是在2018年大红大紫的Bret模型能够强力有效提取词嵌入表达的主要原因之一，GAT可以说是注意力机制在图数据当中的应用。想详细了解注意力机制的读者，可阅读这篇：Attention Is All You Need
  注意力机制的三要素有Query, Source 和 Attention Value,我们可以很自然地想到,将Query设置为当前中心节点，Source设置为邻居节点，而Value就是聚合后的节点表征。
定义节点$v_i$在第$l$层的特征表示为$h_i$,$h_i\in R^{d(l)}$,$d(l)$为该层的特征维度，聚合后的新节点为$h_i^{{}^{\prime }}$。

Fig2 左图：权重a_ij（由节点j到节点i）的计算过程 右图：多头的注意力机制聚合示意图(3种不同颜色的箭头表示3头的注意力机制)

邻居节点$v_j$聚合到$v_i$的权重系数$e_{ij}$为：
$$e_{ij}=a(W{h}_i,W{h}_j)$$
输入是节点集合$h=\{h_1,h_2...h_N\}$,$h_i\in {\mathbb{R}}^F$
输出是新的节点集合$h^{{}^{\prime }}=\{h_1^{{}^{\prime }},h_2^{{}^{\prime }}...h_N^{{}^{\prime }}\}$ ,$h_i^{{}^{\prime }}\in {\mathbb{R}}^{F^{{}^{\prime }}}$
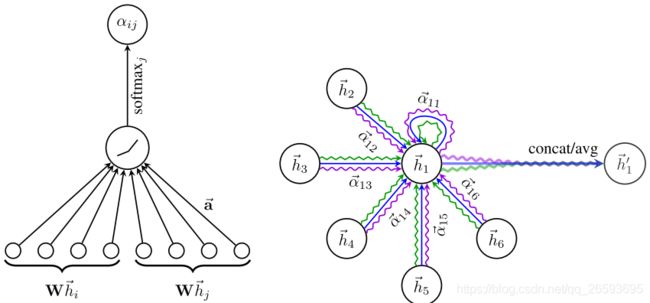
$W\in {\mathbb{R}}^{F\times F^{{}^{\prime }}}$是该层节点特征变换的权重参数.$a(\cdot )$是计算两个节点相关度的函数,比如使用内积作为相关度，文章作者选择了一个单层的全连接层，||表示拼接操作。如Fig2 的左图所示，图中的$a\in {\mathbb{R}}^{2F^{{}^{\prime }}}$，注意：对于节点$v_i$来说，$v_i$也是自己的邻居。
$$e_{ij}=LeakyReLU(a^T[W{h}_i||W{h}_j])(4)$$
为了使不同节点间的权重系数易于比较，我们使用softmax函数对所有计算出的权重进行归一化:
$$a_{ij}={softmax}_i(e_{ij})=\frac{exp(e_{ij})}{{\sum }_{v_k\in {\mathcal{N}}_{v_i}}exp(e_{ik})}(5)$$
$a_{ij}$就是我们的所求，即聚合的权重系数，softmax函数保证了所有系数的和为1，将公式（4）与公式（5）合并，得到计算权重系数完整的表达式:
$$a_{ij}=\frac{exp(LeakyReLU(a^T[W{h}_i||W{h}_j]))}{{\sum }_{v_k\in {\mathcal{N}}_{v_i}}exp(LeakyReLU(a^T[W{h}_i||W{h}_j])}(6)$$
计算完上述归一化注意力系数后，再计算与之对应的特征的线性组合，作为每个节点的最终输出特征。
应用非线性激活函数:
$$h_i^{{}^{\prime }}=\sigma \left(\sum _{v_j\in \mathcal{N}(v_i)}{a}_{ij}W{h}_j\right)(7)$$
更近一步提高注意力层的表达能力，加入多头的注意力机制，对于上式调用K租相互独立的注意力机制，最后将输出拼接在一起，如Fig2 中右图所示：
$$h_i^{{}^{\prime }}=|{|}_{k=1}^K\sigma (\sum _{v_i\in \mathcal{N}(v_i)}{a}_{ij}^{(k)}{W}^k{h}_j)(7)$$
如果是最后一层的话可直接取每一头的平均进行聚合。

总结

  GAT这是一种新型的卷积式神经网络，它利用自注意力机制对邻居节点的重要性加以预测，使模型具有更好的性能和鲁棒性。GAT在计算上不需要昂贵的matrix运算，其得到F’个特征需要的算法复杂度为$O(|V|F{F}^{{}^{\prime }}+|E|F^{{}^{\prime }})$，可并行运算图中的所有节点，对于邻居节点的信息抽取能力比LSTM要好。
优点：

• 模型有效，且鲁棒性好
• 不用一次计算整张图，可批次和并行训练
• 具有很强的可解释性

R-GCNs(Relational Graph Convolutional Networks)

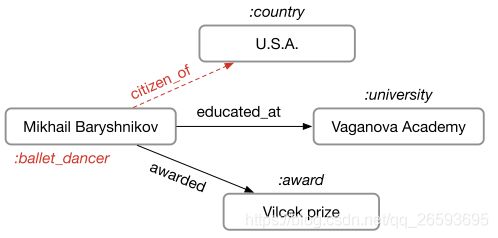
  上面两种模型主要是应用于同构图和无向图的聚合模型，而接下来介绍的R-GCN针对的是异构图与有向图的数据结构，它可以解决关系型数据的知识推理问题，在知识图谱(Knowledge Graph)中有广泛的应用前景。
关系型数据：

• 有权有向
• 节点自身属性

知识推理：

• 实体属性推理
• 连边关系预测

Fig3 关系型数据：节点是标记实体，边是标记的关系类型，红色显示的边和节点标签是需要推断的缺失信息

核心公式给出如下:
$$h_i^{i+1}=\sigma (\sum _{r\in \mathcal{R}}\sum _{j\in {\mathcal{N}}_i^r}\frac{1}{c_{i,r}}{W}_r^{(l)}{h}_j^{(l)}+W_0^{(l)}{h}_i^{(l)})(8)$$

• ${\mathcal{N}}_i^r$表示与节点$v_i$具有$r$关系的邻居节点集合
• $c_{i,r}$是归一化因子，可学习也可自行设定，如$c_{i,r}=|{\mathcal{N}}_i^{(r)}|$

基于上述公式描述，我们可以得到以下信息：

• 每层节点特征都是由上一层节点特征和节点的关系（边）得到；
• 节点的邻居节点特征和自身特征进行加权求和得到新的特征；
• 保留了节点自身的信息考虑自环
• 与 GCN 不同的地方在于 R-GCN 会考虑边的类型和方向

下图 Fig4 描述了R-GCN聚合邻居操作的示意图

Fig4 R-GCN模型中跟新单个节点实体(红色)的示意图

这里对于每种关系，我们用rel_i表示，同时，考虑关系的正向与反向，关系分为in 和out（有向性），每种关系$r$对应一组邻接的实体节点集合 {$v_j$}

模型需要学习关系映射矩阵$W_r$,在一个典型的关系图数据中，往往包含大量错综复杂的关系，如果为每一种关系都学习一组权重，那么R-GCN的参数将会非常庞大，同时由于不同关系的节点数量不一，重要程度不同，这大大增加了过拟合的风险，为了避免这种情况，作者提出了两种分离的正则化方法。
1、对$W_r$进行基函数分解（basis decomposition) ，其本质就一组基的线性组合,即:
$$W_r^{(l)}=\sum _{b=1}^B{a}_{rb}^{(l)}{V}_b^{(l)}(9)$$

• $V_b^{(l)}\in R^{d^{(l+1)}\times d^{(l)}}$为基
• $a_{rb}^{(l)}$为分解系数
• B为超参，控制基的个数

2、块分解（block diagonal decomposition）：
$$W_r^{(l)}=\underset{b=1}{\overset{B}{⨁}}{Q}_{br}^{(l)}(10)$$

• $W_r^{(l)}$是块对角阵$diag(Q_{1r}^{(l)},...,Q_{Br}^{(l)})$其中$Q_{br}^{(l)}\in {\mathbb{R}}^{d^{(l+1)/B}\times (d^{(l)}/B)}$

公式（10）的块分解可以看作是对每种关系类型的权值矩阵的稀疏性约束，即假设潜在的特征可以被分组到一组变量中，这些变量在组内比在组间耦合得更紧密。

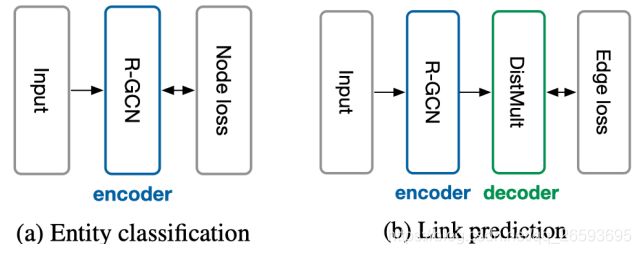
任务

  R-GCN可以作为node的编码层，通过聚合提取图谱中实体之间的关系，为下游任务提供节点嵌入表示。知识推理主要包括两类任务，Entity classificatio(实体分类)与关系预测(Link prediction)，由于本次主要介绍GCN的几种变体，这里就不对如何做推断任务过多展开，感兴趣的读者可以阅读原文Modeling Relational Data with Graph Convolutional Networks。

Fig5 实体分类(左)与关系预测(右)模型结构图

关系图卷积的相关代码可参考Graph Convolutional Networks for relational graphs,是基于keras框架和Theano后台实现的，上手还是非常简单的。

总结

  R-GCN将图卷积运用到关系型数据当中，对异构图和有向图中节点之间的关系进行了有效的定义，解决了利用GCN来处理图结构中不同边关系对节点的影响。但是对于真实场景下的关系图是非常复杂的，文章中虽然对关系矩阵做了分解，降低了学习参数量，但是没有很好地考虑一些超级节点和无效关系的处理，未来的工作可以针对这部分展开，增加模型的泛化能力和鲁棒性。

思考

  上述介绍的几种GNN变体，对于节点的嵌入表示研究了不同的聚合方式，其结构的本质都是消息传播（邻居节点根据一定的规则将特征或者信息，注入到目标节点上，就是所谓的信息传递机制）。通过消息传递的方式，能将节点信息更准确的表达，将节点之间隐藏的关系信息注入到节点当中，为下游任务提供了有效的先验知识。通用的GNN模型扩展框架主要有3种类型分别是：消息传播神经网络(Message Passing Neural Network,MPNN)、非局部神经网络(Non-Local Neural Network,NLNN)、图网络(Grap Network,GN), 之后有时间，将会总结这三种通用框架的一般形式。

参考文献

[1] M. Schlichtkrull, T. N. Kipf, P. Bloem, R. van den Berg, I. Titov, and M. Welling, “Modeling Relational Data with Graph Convolutional Networks,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 10843 LNCS, no. 1, pp. 593–607, 2018.

[2] M. Schlichtkrull, T. N. Kipf, P. Bloem, R. van den Berg, I. Titov, and M. Welling, “Modeling Relational Data with Graph Convolutional Networks,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 10843 LNCS, no. 1, pp. 593–607, 2018.

[3] M. Schlichtkrull, T. N. Kipf, P. Bloem, R. van den Berg, I. Titov, and M. Welling, “Modeling Relational Data with Graph Convolutional Networks,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 10843 LNCS, no. 1, pp. 593–607, 2018.

[4] 《深入浅出图神经网络：GNN原理解析》刘忠雨，李彦霖，周洋， 机械工业出版社

[5] CSDN博客：GraphSAGE：Inductive Representation Learning on Large Graphs 论文详解 NIPS 2017