基于HMM+维特比算法的词性标注实验 附完整C++实现代码

一、理论描述

1.在特定条件下，系统在时间t的状态只与其在时间t-1的状态相关 。这一随机过程称为马尔可夫过程。

2.一个马尔可夫模型由三个部分组成：若干个状态；初始概率；转移概率矩阵。马尔可夫模型中，每个状态代表了一个可观察到的事件，因此如果知道某一事件的观察序列，可应用马尔可夫模型这一统计模型。

3.当事件是不可直接观测到的，就称事件是隐状态。而可观察事件的状态为可观察状态。隐马尔可夫模型用于估算可观察事件背后的事件的概率，被认为是解决大多数自然语言处理问题最快速、有效的方法; 成功解决了复杂的语音识别、机器翻译等 问题;

4.一个隐马尔可夫模型由五部分组成：状态集合（观测序列）；输出结果（隐状态序列）；转移概率分布；发射概率分布；初始状态；

5.隐马尔可夫模型的三个主要应用：（1）. 给定一个隐马尔科夫模型M=(A,B)，如何有效计算某个观测序列O出现的概率，即计算P(O|M) (A表示转移概率，B表示发射概率) ；（2）. 给定一个观测序列O和一个HMM模型M，寻找最好的隐序列Q以便最好的解释观测值 (解码) （3）. 依据给定的观测序列O以及HMM模型中的状态集合，学习最佳HMM参数模型A和B(学习)
针对寻找最佳隐序列（HMM的第二个应用），引入Viterbi算法：依据最后一个时刻中概率最高的状态，逆向通过找其路径中的上一个最大部分最优路径，从而找到整个最优路径。

二、算法描述

本文实现隐马尔可夫模型+维特比算法，具体算法描述如下：
对本题给出的表格数据进行Laplace方法进行平滑处理后得到转移矩阵及发射矩阵

转移矩阵：

发射矩阵

将矩阵及初始概率的值以数组方式存放

定义转移概率矩阵tp，发射概率矩阵ep，数组viterbi[6][6]计算维特比算法中每个状态节点的概率值

计算转移概率分布和发射概率分布

先由初始概率发射概率 计算出第一个单词标注为第i种词性的概率值viterbi[0][i]
Viterbi[0][i]=1.0original_p[i]ep[i][ind[0]];
//第i种词性的初始概率由第i种词性转移到第0个单词的发射概率

然后在两层循环里
for(int i=0;i<6;i++){
for(int j=0;j<6;j++){
}
}
计算每一个状态节点的值viterbi[i][j] 表示为第i个单词标注为第j种词性的概率
由隐马尔可夫模型，系统在第i天的状态与系统在第i-1天的状态有关；
第三层循环枚举前一天的所有词性标注结果的情况k(0<=k<6)，计算viterbi[i-1][k]tp[k][j];//第i-1个单词标注为词性k的最大概率值由词性k转移到词性j的转移概率
得到的k个值取最大值mp，并记录对应的索引mp_id
用该最大值乘以由词性j到第i个单词的发射概率ep[j][ind[i]]作为当前状态节点的最大概率值
Viterbi[i][j]=mp*ep[j][ind[i]];
并记录路径（当前状态的前一列保存的节点为词性k）

最后一列的k种概率值 取最大者作为答案，此时的答案即为得到的该最大概率隐序列的概率值ans；
ans_id为该隐序列的最后一个元素。
通过path数组的向前回溯即可得到隐序列的倒数第二个元素、倒数第三个元素…
反向存储在output数组中 最后正向输出答案即可

三、详例描述
以“The bear is on the move”为例，详细描述维特比算法如下：

‘The’被标注为词性AT、BEZ、IN、NN、VB、PERIOD的概率分别为：
0.19998
9.92753e-06
1.82083e-05
0.000367647
0.00159574
2.04847e-06
‘bear’被标注为AT的概率（状态viterbi[1][0]）
Max=0;
for(int k=0;k<6;k++){
Max=max(Max,viterbi[0][k]*tp[k][0]);//前一个单词（第0个）被标记为词性k的概率viterbi[0][k]由词性k到当前状态的词性（AT的索引为0）的转移概率tp[k][0]
}
Viterbi[1][0]=Maxep[0][ind[1]]
取其中的最大值并乘上由当前状态的词性（当前状态的词性为AT——索引为0）转移到当前状态的单词(当前为第1个单词（从0开始）——索引为ind[1])的发射概率

上述为第0行第1列状态节点的计算过程，其含义是单词bear被标注为词性AT的最大概率.

四、软件演示
将作业的实验结果截图，并对结果进行阐述和分析。
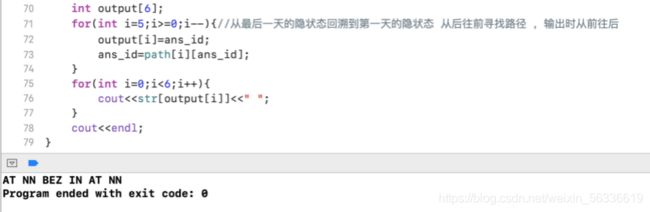
针对本题目例句输出词性标注序列如下：
The bear is on the move
AT NN BEZ IN AT NN

五、本次作业中存在的问题和总结

（一）本次作业中存在哪些问题，可以在此列出来；

1.编程语言的选择：一开始选择的是Python语言，因为Python自带的argmax()函数可以返回最大值的索引值，十分方便。但是概率分布矩阵中的值是小数，Python默认的数据类型是float,遇到了’float’ object is not subscriptable 的报错。转换成double类型后遇到‘IndexError: invalid index to scalar variable.’的报错，因此最后选择了C++语言完成本次作业;

2.一开始输出答案序列出错了，犯了很愚蠢的错误想当然地
for(int i=0;i<6;i++){
Cout< }
作为答案，后来联想到维特比算法和算法课上学习的动态规划上求最短路径问题的算法很相似，path[][]数组的想法也是运用之前算法课的动态规划思维而设的，因此应该和动态规划问题一样不断的更新一个指针p
While(p!=-1){//初始化next数组的值为-1 因此循环到p==-1时代表已经遍历到起点 应该结束
cout< p=next[p];
}

（二）本次作业中有哪些可以分享的，可以在此列出来。
如何通俗地讲解 viterbi 算法？https://www.zhihu.com/question/20136144

详细实现代码：

#include
using namespace std;
//Laplace方法进行数据平滑处理后的转移矩阵和发射矩阵
int transistion_matrix[6][6]={{1,1,1,48637,1,20},{1974,1,427,188,1,39},{43323,1,1326,17315,1,186},{1068,3721,42471,11774,615,21393},{6073,43,4759,1477,130,1523},{8017,76,4657,1330,955,1}};

int emission_matrix[6][8]={{1,1,1,1,1,1,69017,1},{1,10066,1,1,1,1,1,1},{1,1,1,5485,1,1,1,1},{11,1,37,1,383,109,1,1},{44,1,134,1,1,5,1,1},{1,1,1,1,1,1,1,48810}};
//初始概率
double original_p[6]={0.2,0.1,0.1,0.2,0.3,0.1};
int transistion_sum[6],emission_sum[6];
int ind[6]={6,0,1,3,6,2};//待标注句子“The bear is on the move”共6个单词 第i个单词的下标索引值ind[i]

string str[6]={"AT","BEZ","IN","NN","VB","PERJOD"};

double tp[6][6],ep[6][8];//tp转移概率矩阵 ep发射概率矩阵
double viterbi[6][6];//待标注句子共有6个单词，语料库共有6种词性 共36个状态节点
int path[6][6];//记录路径
int main()
{
    for(int i=0;i<6;i++){
        for(int j=0;j<6;j++){
            transistion_sum[i]+=transistion_matrix[i][j];
        }
    }
    for(int i=0;i<6;i++){
        for(int j=0;j<8;j++){
            emission_sum[i]+=emission_matrix[i][j];
        }
    }
    //转移概率及发射概率的计算
    for(int i=0;i<6;i++){//转移概率矩阵 每行概率和为1
        for(int j=0;j<6;j++){
            tp[i][j]=1.0*transistion_matrix[i][j]/transistion_sum[i];
        }
    }
    for(int i=0;i<6;i++){//发射概率矩阵 每行概率和为1
        for(int j=0;j<8;j++){
            ep[i][j]=1.0*emission_matrix[i][j]/emission_sum[i];
        }
    }
    //HMM + VERTEBI 算法
    for(int i=0;i<6;i++){//计算第一列的节点的值 初始概率*发射概率
        viterbi[0][i]=1.0*original_p[i]*ep[i][ind[0]];//第一列对应的单词（句子的第0个单词）the的下表索引值是6 ind[0]==6
    }
    for(int i=1;i<6;i++){//第i列 句子的第i个单词的词性
        for(int j=0;j<6;j++){//可标注的词性共6种可选
            double mp=0;//temporary maxmium
            int mp_id=-1;
            for(int k=0;k<6;k++){//遍历更新最大值
                if(viterbi[i-1][k]*tp[k][j]>mp){
                    mp=viterbi[i-1][k]*tp[k][j];
                    mp_id=k;
                }
            }
            viterbi[i][j]=mp*ep[j][ind[i]];//记录前向最大概率值
            path[i][j]=mp_id;
        }
    }
    

    double ans=0;
    int ans_id=0;最后一个单词的词性
    
    for(int i=0;i<6;i++){
        if(viterbi[5][i]>ans){
            ans=viterbi[5][i];
            ans_id=i;
        }
    }
    
    int output[6];
    for(int i=5;i>=0;i--){//从最后一天的隐状态回溯到第一天的隐状态 从后往前寻找路径 ，输出时从前往后
        output[i]=ans_id;
        ans_id=path[i][ans_id];
    }
    for(int i=0;i<6;i++){
        cout<<str[output[i]]<<" ";
    }
    cout<<endl;
}

/*
 The bear is on the move
 AT  NN  BEZ IN AT  NN
 
 */