多层神经网络
为了解决线性不可分的问题,可以在输入层和输出层之间增加隐含层。
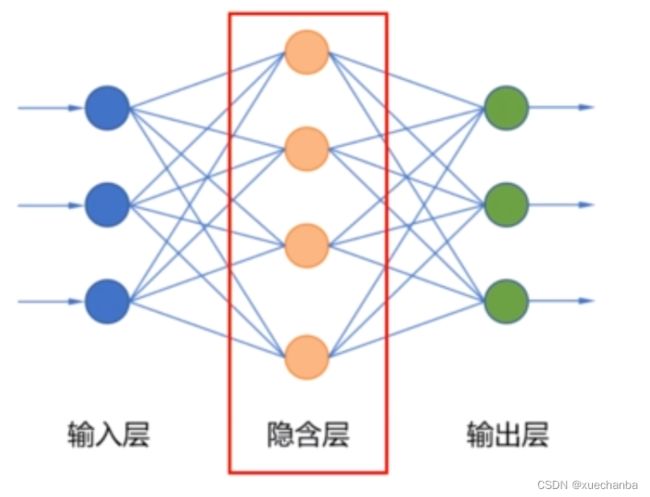
隐含层和输出层一样,也是具有计算能力的功能神经元。这种增加了隐含层的神经网络就被称为多层神经网络。
在前面说过,与或非运算的结果都是线性可分的。可以通过下图第四个小图所示的感知机来实现。
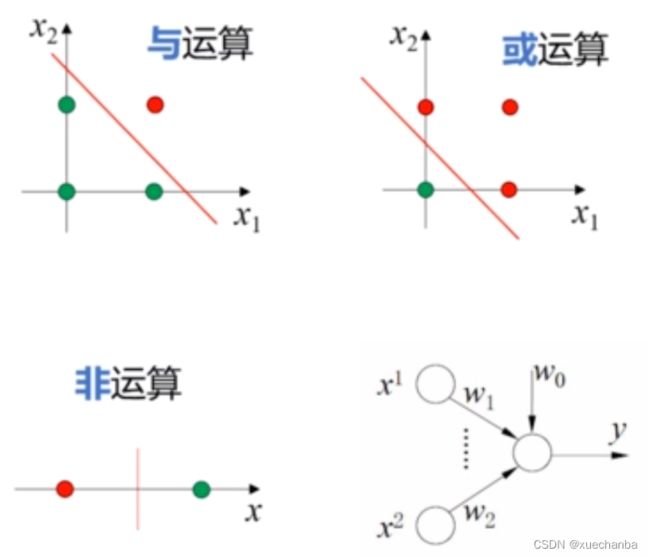
给出合适的权值向量 W ,就可以实现与运算、或运算、非运算。
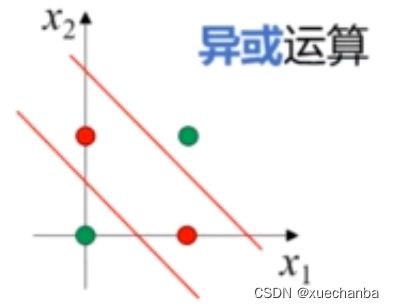
而异或运算
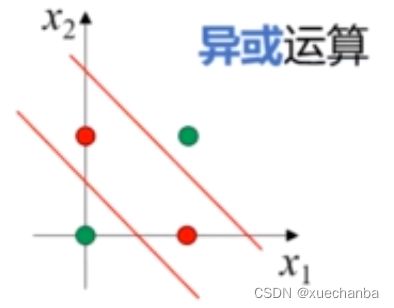
则是非线性可分的。至少需要两条直线采可以将其分开。
为了实现对异或结果的分类,可以构建如下图所示的含有隐藏层的神经网络。
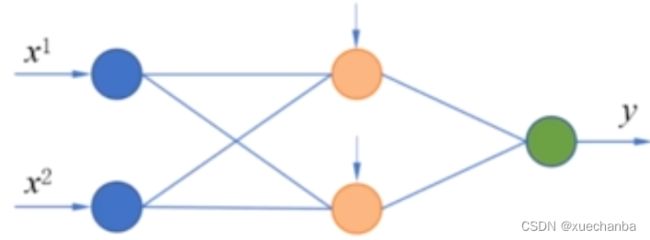
它其实是由
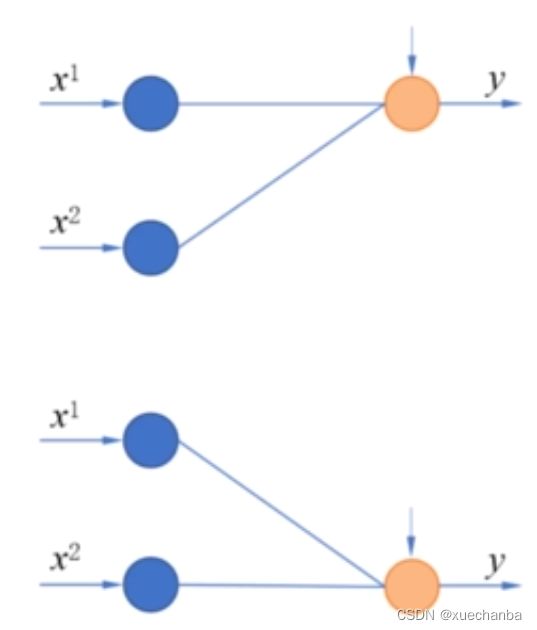
这样的两个感知机组合在一起构成的神经网络。
先来看第一个感知机,
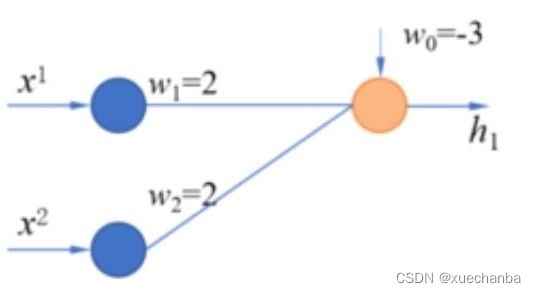
它的两个权值都是2,阈值为-3,这是线性模型的表达式 z1 和感知机的表达式 h1
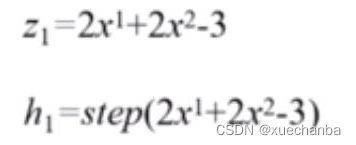
当输入(x1,x2)后,得到 z1 和 h1 的结果。

根据上面的输入和输出,可以发现,全1得1,有0得0,从而总结出,这其实就是一个与运算。从而,
![]()
下图为对应的四个点的坐标和分类决策边界。
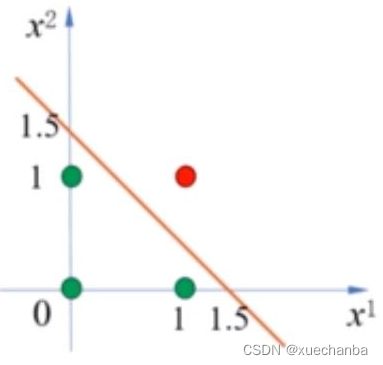
下图为第二个感知机,
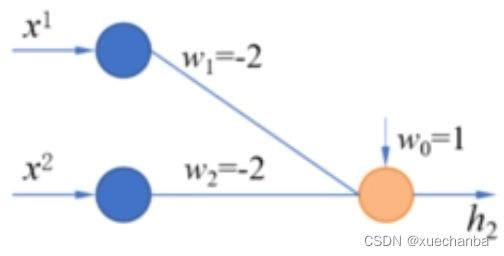
它的两个权值都是-2,阈值为1,这是线性模型的表达式 z1 和感知机的表达式 h1
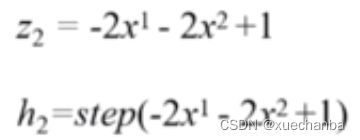
当输入(x1,x2)后,得到 z1 和 h1 的结果。
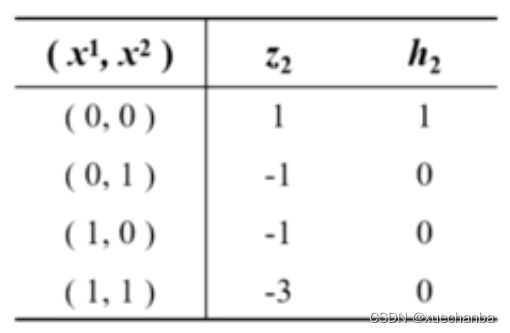
根据上面的输入和输出,可以发现,这其实就是或非运算。从而,
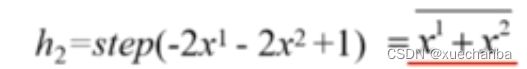
下图为对应的四个点的坐标和分类决策边界。
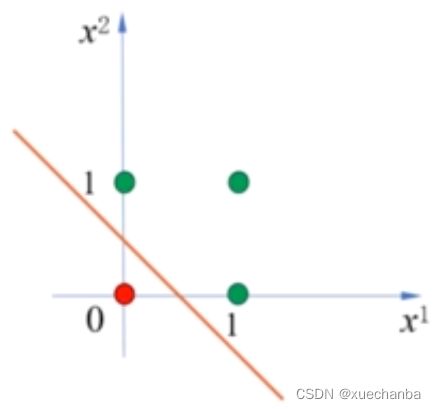
下面,将上面的两个感知机组合在一起,它们的权值和阈值不变,
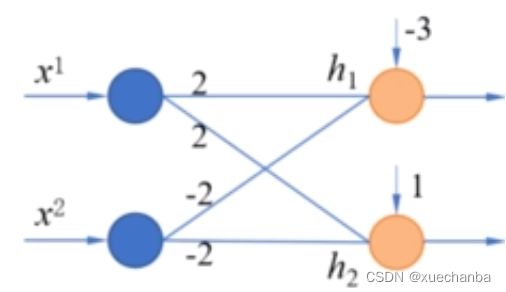
这两个神经元的输出再作为下一层神经元的输入
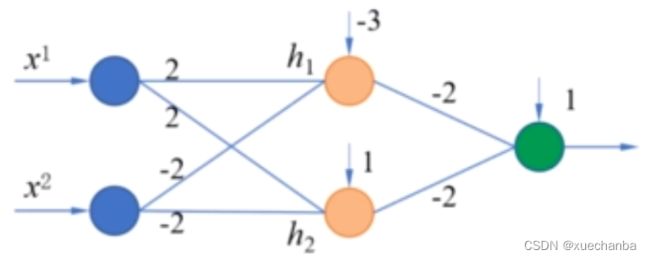
增加的这一层权值和阈值与第二个感知机一样,因此它也是实现或非运算。

当输入(x1,x2)为(0,0)或 (1,1) 时,输出为0,当输入(x1,x2)为(1,0)或 (0,1) 时,输出为1。
从而这两类点也就被分开了,而且符合异或运算的规则。
在这个神经网络中,
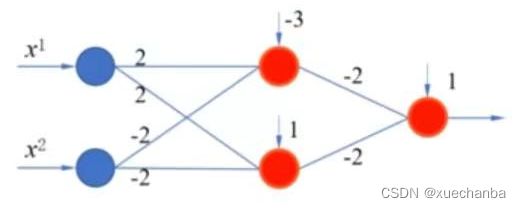
一共使用了3个有计算能力的神经元,

那么为什么增加隐含层就可以分开这两类点呢?
因为一个感知机对应一条直线,在这个问题中,使用一个直线无法将两类点给分开,但是使用两根直线就可以。
因此,首先使用两个感知机分别实现两个线性分类器,
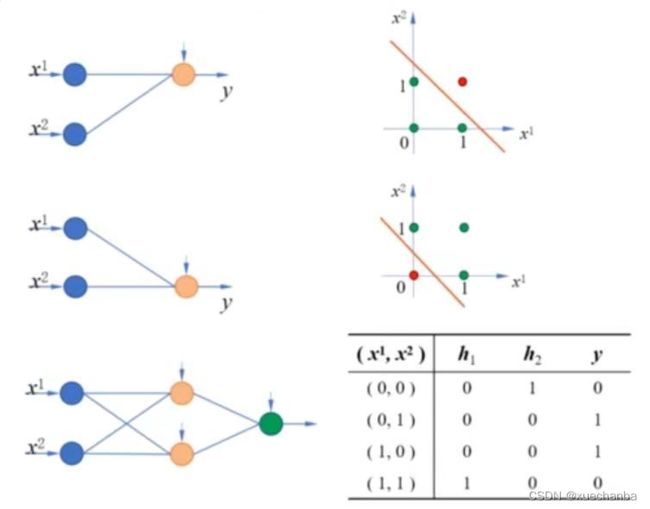
第一个感知机实现了与运算,第二个感知机则实现了或非运算,接着再它们的后面再连接一个神经元,对它们的结果再进行一次或非运算,就得到了异或运算的结果。
使用逻辑代数运算,也可以得到同样的结果。
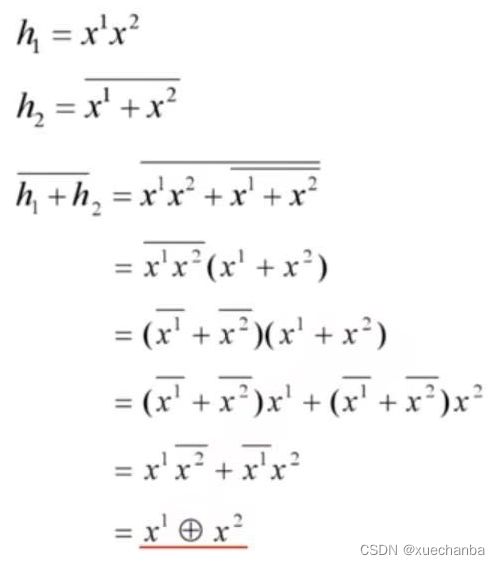
也可以使用其他的逻辑代数运算来实现,例如先实现或运算,再进行与非运算,最后再对它们的结果进行一次与运算。
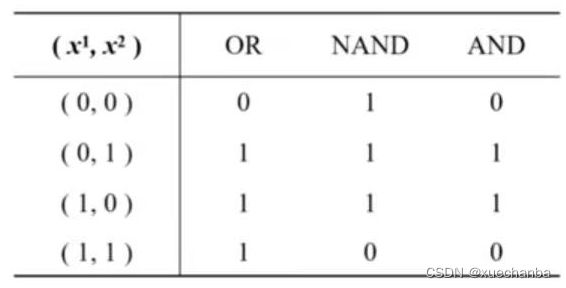
因此,可以调整调整神经网络中的权值参数,使得这三个神经元分别实现
或运算、与非运算和与运算。
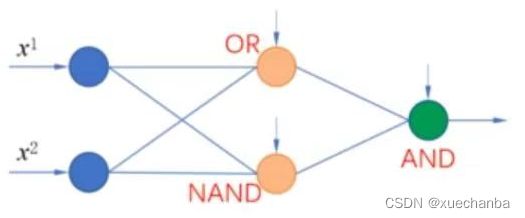
最终,可实现异或运算。
更多的线性不可分数据集,需要弯曲的边界线,
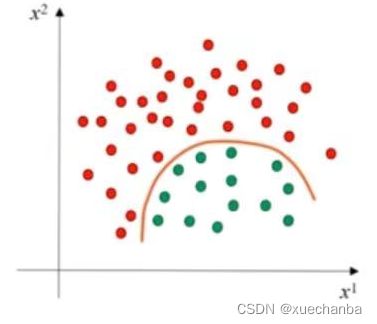
才能将它们区分开来。
这种弯曲的分界线,可以看作是
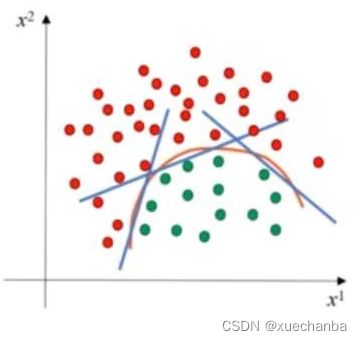
多条直线组合的结果。
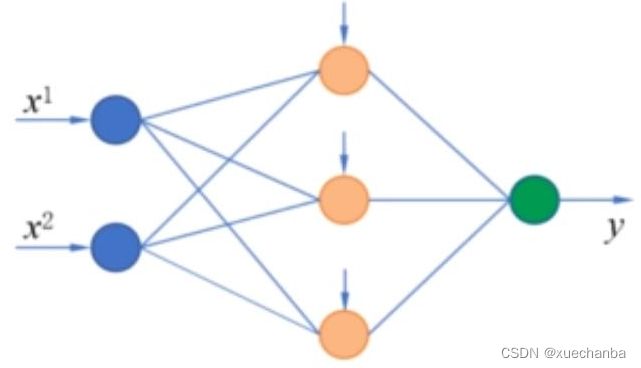
只要有足够多的直线,拼在一起,就可以表示出更复杂的边界,其中,每一条直线可以通过一个感知机来实现,在它们的后面再加上一个神经元把这些直线组合起来,就可以实现对非线性问题的分类了。
再来看下图,
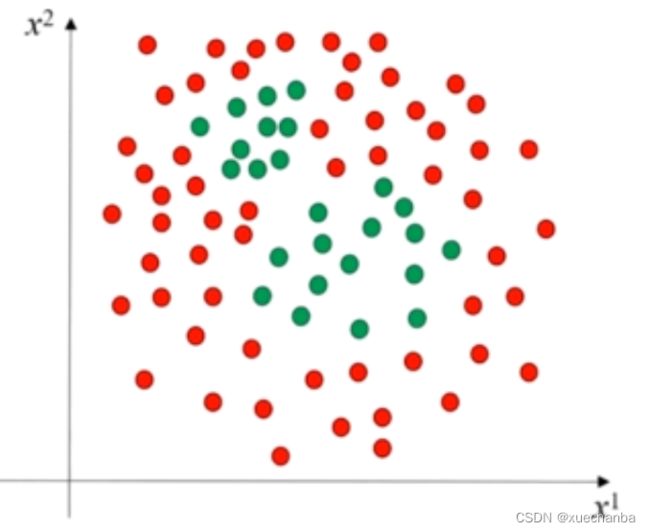
可以通过一个六边形区域将绿色的点区分开来。
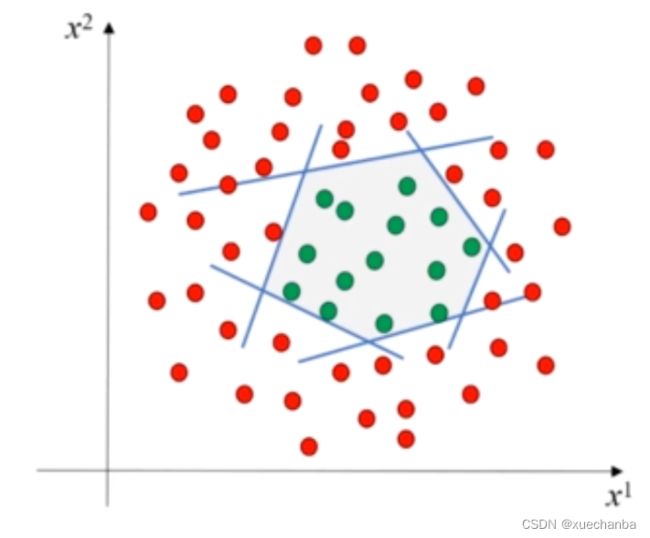
因此,可以设计一个这样的神经网络来进行实现。
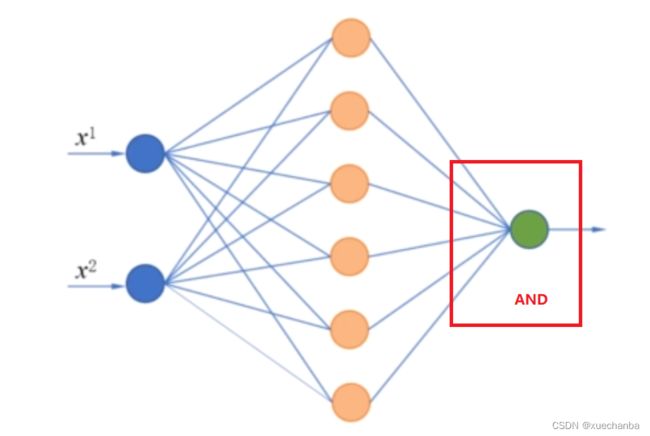
隐含层中有六个神经元,其中每条神经元就对应一条分类直线,输出层神经元使用与逻辑将它们连接起来,就可以实现对这个非线性数据集的分类。
为了更加的简洁,在这个图中,我们没有标记出表示阈值的箭头。只要知道每个神经元都有阈值这个参数就可以了。
如果情况再复杂一些,比如下图所示的数据集,通过神经网络可以将它们区分开来吗?
首先,来看下数据的分布,
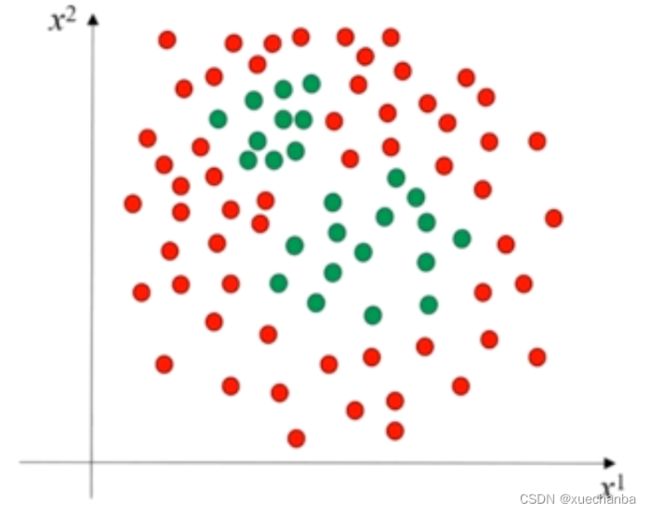
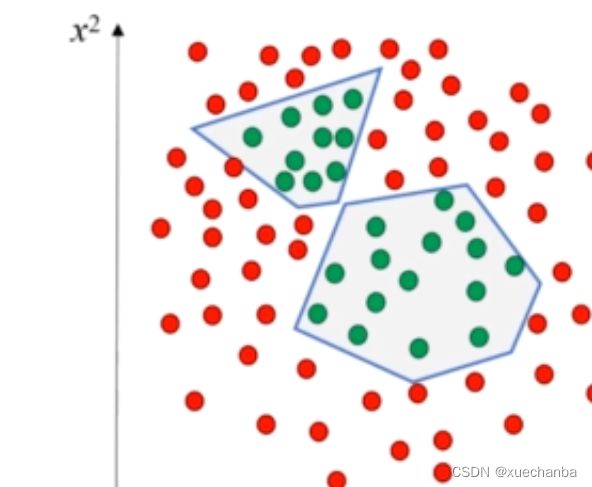
为了实现对这个数据集的分类,
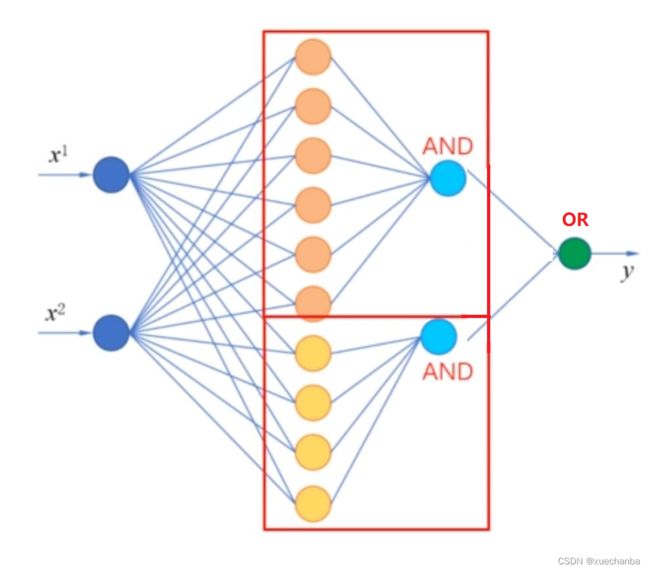
这个神经网络需要两个隐含层分别构成一个六边形的分类器和一个四边形的分类器,最后再需要一个神经元实现逻辑或,把它们组合在一起,就实现了对这个数据集的分类。
在理论上,如果神经网络中有足够多隐含层,每个隐含层中有足够多的神经元,神经网络就可以表示任意复杂的函数或空间分布。
特别需要说明的是,在上面举这么多例子的目的是为了说明为什么在神经网络中增加隐含层就能够实现非线性分类,在实际应用中,是完全不需要这样刻意精确的设计神经网络隐含层的结构和它的权值的,通常只需要经验大概确定隐含层的层数和每层中神经元的个数,然后使用训练数据集通过迭代算法自动的去寻找使得网络性能最佳的权值,如果训练效果不好,就试着去改变隐含层的层数,或者改变其中的神经元个数,再进行训练,直到得到满意的结果为止。
神经网络中的层数和每层中神经元的个数是比较灵活地,在这个例子中,如果只使用一个隐含层,只要这层中有足够多的神经元也可以得到比较好的效果。比如下图是由10个神经元构成的十边形区域,实现了对数据集的分类。
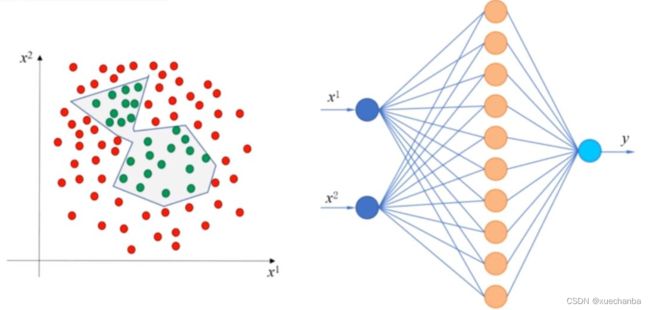
因此,有人把神经网络形容成一个黑盒,我们只需要把数据喂进去,并且告诉它,我们想要的结果,它就会根据学习算法,自动更新所有连接上的权值,尝试去拟合我们所期望的输出。所有这些神经元,最后实现了一个复杂的函数,来完成我们的任务。而这个复杂的函数,究竟是什么,每个神经元究竟实现了一个什么样的运算,我们是不需要知道的,这就像教一个小孩识字,我们只需要每天反复的给他看十次卡片,并告诉他这些字是什么,经过一点时间之后,他就认识这些字了,我们的目的也就达到了,而在他的大脑中,每一个神经元是怎样被激发,神经元之间又是如何连接的,我们可以不去关心。
在前面看到的这些神经网络,都是前馈式神经网络,
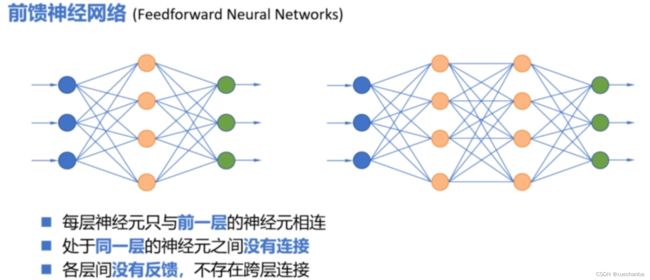
在这种网络结构中,神经元分层排列,每层神经元只与前一层的神经元相连。接收前一层的输出作为本层的输入,同一层的神经元之间互相没有连接,各层间的信息传送没有反馈,也不存在跨层连接。
观察这些神经网络,还可以发现另外一个特点,
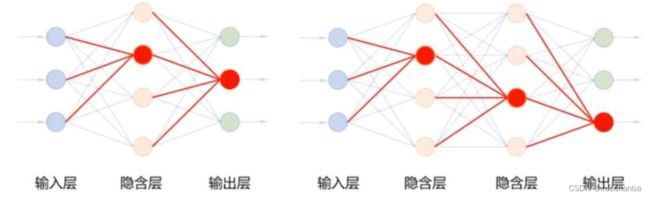
每一层中的任何一个节点都和它后面一层中的所有节点连接。
此外,如果第 n 层中的每个节点,都接收来自 n-1 层中所有节点的输入。
那么,这种网络结构就被称之为全连接网络。
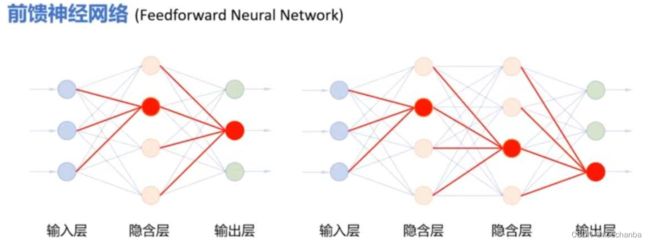
再来区分下前面说的两个多层神经网络,如下图所示。
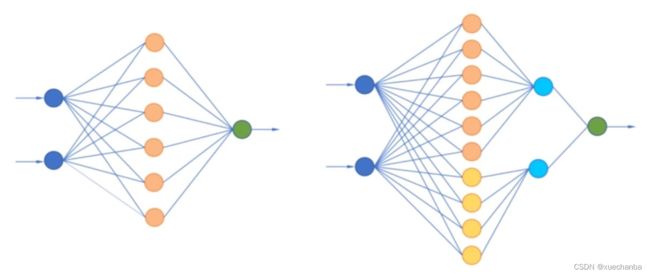
第一个是前馈式神经网络同时也是全连接网络,而第二个只是前馈式神经网络,而不是全连接网络。
其实,在我们设计神经网络时,如果网络规模不大,可以把它们都设计成全连接网络,在使用数据集训练之后,其中不需要的连接权值就会接近为0,就好像没有连接一样。
总结:人工神经网络只是借鉴了生物神经网络中最基本的特征——神经元以及神经元之间的连接而设计的一种可以通过计算机处理和优化的数学模型,与人类大脑相比,人工神经网络的规模和结构都要简单的多。