NLP学习—22.Transformer的代码实现
文章目录
-
-
- 引言
- 一、准备工作
- 二、背景介绍
- 三、模型结构
-
- 1.Encoder-Decoder结构
- 2.Encoder and Decoder Stacks
-
- 2.1 Encoder
- 2.2 decoder
- 3.Attention
-
- 3.1self-attention
- 3.2 Multi-Head Attention
- 3.3 Attention在模型中的应用
- 4.Feed-Forward
- 5.Embeddings
-
- 5.1 Positional Encoding
- 6.完整模型
- 四、模型训练
- 五、Example
-
- Transformer理论部分
- Transformer代码实现
- 基于Transformer的机器翻译实战
引言
Transformer是如今几乎所有的预训练模型的基本结构。也许我们平时更多的是关注如何更好的利用已经训练好的GPT、BERT等模型进行fine-tune,但是同样重要的是,我们需要了解这些强力的模型具体是如何构建的。所以本文我们主要研究如何在PyTorch框架下用代码实现 “Attention is All You Need” 论文中原始Transformer的结构。
一、准备工作
本文的测试环境是Python 3.6+和PyTorch 1.6
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import math, copy, time
import matplotlib.pyplot as plt
import seaborn
seaborn.set_context(context="talk")
%matplotlib inline
二、背景介绍
当谈及序列模型(sequence modeling),我们首先想到的就是RNN及其变种,但是RNN模型的缺点也非常明显:需要顺序计算,从而很难并行。因此出现了Extended Neural GPU、ByteNet和ConvS2S等网络模型。这些模型都是以CNN为基础,这比较容易并行,但是和RNN相比,它较难学习到长距离的依赖关系。
本文的Transformer使用了Self-Attention机制,它在编码每一词的时候都能够注意(attend to)整个句子,从而可以解决长距离依赖的问题,同时计算Self-Attention可以用矩阵乘法一次计算所有的时刻,因此可以充分利用计算资源。
三、模型结构
1.Encoder-Decoder结构
序列转换模型是基于Encoder-Decoder结构的。所谓的序列转换模型就是把一个输入序列转换成另外一个输出序列,它们的长度很可能是不同的。比如基于神经网络的机器翻译,输入是法语句子,输出是英语句子,这就是一个序列转换模型。类似的包括文本摘要、对话等问题都可以看成序列转换问题。我们这里主要关注机器翻译,但是任何输入是一个序列输出是另外一个序列的问题都可以考虑使用Encoder-Decoder结构。
Encoder将输入序列 ( x 1 , . . , x n ) (x_1,..,x_n) (x1,..,xn)编码成一个连续的序列 z = ( z 1 , . . , z n ) z=(z_1,..,z_n) z=(z1,..,zn)。而Decoder根据 z z z来解码得到输出序列 y = ( y 1 , . . , y m ) y=(y_1,..,y_m) y=(y1,..,ym)。Decoder是自回归的(auto-regressive),它会把前一个时刻的输出作为当前时刻的输入。Encoder-Decoder结构对应的代码如下:
class EncoderDecoder(nn.Module):
"""
A standard Encoder-Decoder architecture. Base for this and many other models.
将encoder的最后一个Block分别传给decoder中的每一个block,然后decoder进行输出生成。
"""
def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
super(EncoderDecoder, self).__init__()
self.encoder = encoder
self.decoder = decoder
self.src_embed = src_embed
self.tgt_embed = tgt_embed
self.generator = generator
def forward(self, src, tgt, src_mask, tgt_mask):
"""
Take in and process masked src and target sequences.
"""
return self.decode(self.encode(src, src_mask), src_mask, tgt, tgt_mask)
def encode(self, src, src_mask):
return self.encoder(self.src_embed(src), src_mask)
def decode(self, memory, src_mask, tgt, tgt_mask):
return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)
class Generator(nn.Module):
"""
Define standard linear + softmax generation step.
映射到vocab维度并做softmax得到生成每个词的概率
"""
def __init__(self, d_model, vocab):
super(Generator, self).__init__()
self.proj = nn.Linear(d_model, vocab)
def forward(self, x):
return F.log_softmax(self.proj(x), dim=-1)
EncoderDecoder定义了一种通用的Encoder-Decoder架构,具体的encoder、decoder、src_embed、target_embed和generator都是构造函数传入的参数。这样我们做实验更换不同的组件就会更加方便。
解释一下各种参数的意义:encoder、encoder分别代表编码器和解码器;src_embed、tgt_embed分别代表将源语言、目标语言的ID序列编码为词向量(embedding)的方法;generator则是根据解码器当前时刻的隐状态输出当前时刻的词,上面已给出具体的实现方法(即Generator类)。
Transformer模型也遵循着Encoder-Decoder的架构。它的Encoder是由N=6个相同的EncoderLayer组成,每个EncoderLayer包含一个Self-Attention Sublayer层和一个Feed-Forward Sublayer层;而它的Decoder也是由N=6个相同的DecoderLayer组成,每个DecoderLayer包含一个Self-Attention Sublayer层、一个Encoder-Decoder-Attention Sublayer层和一个Feed-Forward Sublayer层。下面展示Transformer整体架构:
2.Encoder and Decoder Stacks
2.1 Encoder
前面提到Encoder是由N=6个相同结构的EncoderLayer堆叠而成,所以我们定义Encoder的代码如下:
def clones(module, N):
"""
Produce N identical layers.
"""
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
class Encoder(nn.Module):
"""
Core encoder is a stack of N layers.
"""
def __init__(self, layer, N):
super(Encoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, mask):
"""
Pass the input (and mask) through each layer in turn.
"""
for layer in self.layers:
x = layer(x, mask)
return self.norm(x)
也就是Encoder会把传入的layer深拷贝N次,然后让传入的Tensor依次通过这N个layer,最后再通过一层 Layer Normalization。
class LayerNorm(nn.Module):
"""
Construct a layernorm module, see https://arxiv.org/abs/1607.06450 for details.
"""
def __init__(self, features, eps=1e-6):
super(LayerNorm, self).__init__()
self.a_2 = nn.Parameter(torch.ones(features))
self.b_2 = nn.Parameter(torch.zeros(features))
self.eps = eps
def forward(self, x):
mean = x.mean(-1, keepdim=True)
std = x.std(-1, keepdim=True)
return self.a_2 * (x - mean) / (std + self.eps) + self.b_2
按照原论文,每一个EncoderLayer的每一个子层(sub-layer)的输出应该是
L a y e r N o r m ( x + S u b l a y e r ( x ) ) LayerNorm(x+Sublayer(x)) LayerNorm(x+Sublayer(x)),其中Sublayer(x)是对子层结构实现的抽象函数。这里稍微做了一些修改,首先在每一个子层的输出之后加了一个Dropout层,另外一个不同就是把LayerNorm层放到前面了。也就是现在每一个子层实际的输出是:
x + D r o p o u t ( S u b l a y e r ( L a y e r N o r m ( x ) ) ) x+Dropout(Sublayer(LayerNorm(x))) x+Dropout(Sublayer(LayerNorm(x)))
为了加快残差连接的速度,模型中所有的子层(sub-layer),包括Embedding层,将它们的输出维度均设置为 d m o d e l = 512 d_{model}=512 dmodel=512。所以我们有如下代码:
class SublayerConnection(nn.Module):
"""
A residual connection followed by a layer norm.
Note for code simplicity the norm is first as opposed to last.
"""
def __init__(self, size, dropout):
super(SublayerConnection, self).__init__()
self.norm = LayerNorm(size)
self.dropout = nn.Dropout(dropout)
def forward(self, x, sublayer):
"""
Apply residual connection to any sublayer with the same size.
"""
return x + self.dropout(sublayer(self.norm(x)))
上面提到EncoderLayer是由Self-Attention、Feed-Forward这两个子层构成,所以有如下代码:
class EncoderLayer(nn.Module):
"""
Encoder is made up of self-attn and feed forward.
"""
def __init__(self, size, self_attn, feed_forward, dropout):
super(EncoderLayer, self).__init__()
self.self_attn = self_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 2)
self.size = size
def forward(self, x, mask):
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
return self.sublayer[1](x, self.feed_forward)
2.2 decoder
Decoder也是由 N = 6 N=6 N=6个相同结构的DecoderLayer堆叠而成。
class Decoder(nn.Module):
"""
Generic N layer decoder with masking.
"""
def __init__(self, layer, N):
super(Decoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, memory, src_mask, tgt_mask):
for layer in self.layers:
x = layer(x, memory, src_mask, tgt_mask)
return self.norm(x)
前面讲到,一个DecoderLayer除了有和EncoderLayer一样的两个子层,还多了一个Encoder-Decoder-Attention子层,这个子层会让模型在解码时会考虑最后一层Encoder所有时刻的输出。
class DecoderLayer(nn.Module):
"""
Decoder is made of self-attn, src-attn, and feed forward.
"""
def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
super(DecoderLayer, self).__init__()
self.size = size
self.self_attn = self_attn
self.src_attn = src_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 3)
def forward(self, x, memory, src_mask, tgt_mask):
m = memory
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
return self.sublayer[2](x, self.feed_forward)
多出来的这一层Attention子层(代码中是src_attn)实现和Self-Attention是一样的,只不过src_attn的Query来自于前层Decoder的输出,但是Key和Value来自于Encoder最后一层的输出(代码中是memory);而Self-Attention的Q、K、V则均来自前层的输出。
Decoder和Encoder还有一个关键的不同:Decoder在解码第t个时刻的时候只能使用小于t时刻的输入,而不能使用t+1时刻及其之后的输入。因此我们需要一个函数来产生一个Mask矩阵:
def subsequent_mask(size):
"""
Mask out subsequent positions.
"""
attn_shape = (1, size, size)
subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
return torch.from_numpy(subsequent_mask) == 0
上面代码的意思是先用triu函数产生一个上三角矩阵,再利用matrix == 0得到所需要的下三角矩阵。上三角全部都为0,下三角全部都为1。
plt.figure(figsize=(5,5))
plt.imshow(subsequent_mask(20)[0])
3.Attention
3.1self-attention
Attention(包括Self-Attention和普通的Attention)可以看成一个函数,它的输入是Query,Key和Value,输出是一个Tensor。其中输出是Value的加权平均,而权重则来自Query和Key的计算。
论文中首先提到了Scaled Dot-Product Attention,如下图所示:
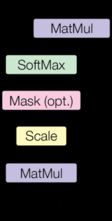
具体计算是先将一组query和所有的keys作点乘运算,然后除以 d k \sqrt{d_k} dk保证后续梯度的稳定性,然后将这些分数进行softmax归一化,作为query和Keys的相似程度,也就是values加权平均的权重,最后将所有values作加权平均作为输出。这里用矩阵直接表示:
![]()
代码如下:
def attention(query, key, value, mask=None, dropout=None):
"""
Compute 'Scaled Dot Product Attention'
"""
d_k = query.size(-1)
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
# 将padding部分赋予很小的数值
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
# 归一化得到attention weight
p_attn = F.softmax(scores, dim=-1)
# dropout
if dropout is not None:
p_attn = dropout(p_attn)
# 返回加权后的vector与attention weight
return torch.matmul(p_attn, value), p_attn
3.2 Multi-Head Attention
论文中非常重要的Multi-Head Attention便是基于Scaled Dot-Product Attention。其实很简单,前面定义的一组Q、K和V可以让一个词attend to相关的词,我们可以定义多组Q、K和V,它们分别可以关注不同的上下文:
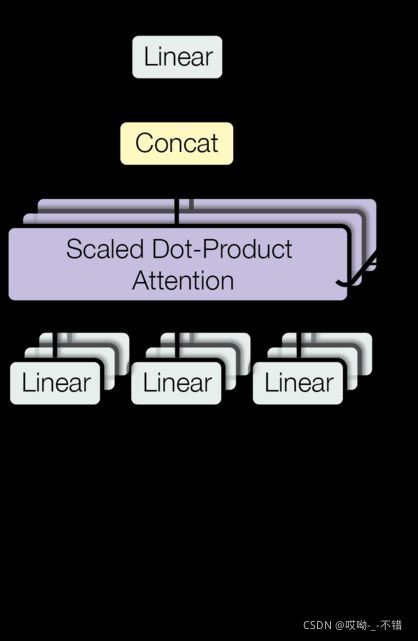
由上图我们可以得到如下计算公式:
M u l t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , . . . , h e a d h ) W O h e a d i = A t t e n t i o n ( Q W i Q , K W i K , V W i V ) MultiHead(Q,K,V)=Concat(head_1,...,head_h)W^O\\head_i=Attention(QW^Q_i,KW^K_i,VW^V_i) MultiHead(Q,K,V)=Concat(head1,...,headh)WOheadi=Attention(QWiQ,KWiK,VWiV)
论文中使用了 h = 8 h=8 h=8个Head,所以此时 d k = d v = d m o d e l / h = 64 d_k=d_v=d_{model}/h=64 dk=dv=dmodel/h=64。虽然此时Head数扩大了8倍,但由于每一个Head的维度缩小了8倍,所以总体的计算成本是基本不变的。
Multi-Head Attention的代码如下:
class MultiHeadedAttention(nn.Module):
"""
Implements 'Multi-Head Attention' proposed in the paper.
"""
def __init__(self, h, d_model, dropout=0.1):
"""
Take in model size and number of heads.
"""
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0
# We assume d_v always equals d_k
self.d_k = d_model // h
self.h = h
self.linears = clones(nn.Linear(d_model, d_model), 4)
self.attn = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
if mask is not None:
# Same mask applied to all h heads.
mask = mask.unsqueeze(1)
nbatches = query.size(0)
# 1) Do all the linear projections in batch from d_model => h x d_k
query, key, value = [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linears, (query, key, value))]
# 2) Apply attention on all the projected vectors in batch.
x, self.attn = attention(query, key, value, mask=mask, dropout=self.dropout)
# 3) "Concat" using a view and apply a final linear.
x = x.transpose(1, 2).contiguous().view(nbatches, -1, self.h * self.d_k)
return self.linears[-1](x)
3.3 Attention在模型中的应用
在Transformer里,有3个地方用到了Multi-Head Attention:
- Decoder的Encoder-Decoder-Attention层。其中query来自于前一层Decoder的输出,而key和value则来自于是Encoder最后一层的输出,这个Attention层使得Decoder在解码时会考虑最后一层Encoder所有时刻的输出,是一种在Encoder-Decoder架构中常用的注意力机制。
- Encoder的Self-Attention层。query,key和value均来自于相同的地方,也就是前层Encoder的输出。
- Decoder的Self-Attention层。query,key和value均来自于相同的地方,也就是前层Decoder的输出,但是Mask使得它不能访问未来时刻的输出。
4.Feed-Forward
除了Attention子层,Encoder和Decoder的每一层还包括一个Feed-Forward子层,也就是全连接层。每个时刻的全连接层是可以独立并行计算的(当然参数是共享的)。全连接层由两个线性变换以及它们之间的ReLU激活组成:
F F N ( x ) = m a x ( 0 , x W 1 + b 1 ) W 2 + b 2 FFN(x)=max(0,xW_1+b_1)W_2+b_2 FFN(x)=max(0,xW1+b1)W2+b2
全连接层的输入和输出都是 d m o d l e = 512 d_{modle}=512 dmodle=512维的,中间隐单元的个数是 d f f = 2048 d_ff=2048 dff=2048。代码实现非常简单:
class PositionwiseFeedForward(nn.Module):
"""
Implements FFN equation.
"""
def __init__(self, d_model, d_ff, dropout=0.1):
super(PositionwiseFeedForward, self).__init__()
self.w_1 = nn.Linear(d_model, d_ff)
self.w_2 = nn.Linear(d_ff, d_model)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
return self.w_2(self.dropout(F.relu(self.w_1(x))))
5.Embeddings
和大部分NLP任务一样,输入的词序列都是ID序列,所以需要有个Embeddings层。
class Embeddings(nn.Module):
def __init__(self, d_model, vocab):
super(Embeddings, self).__init__()
# lut => lookup table
self.lut = nn.Embedding(vocab, d_model)
self.d_model = d_model
def forward(self, x):
return self.lut(x) * math.sqrt(self.d_model)
需要注意的是,在Embeddings层,所有的权重都扩大了 d m o d e l \sqrt{d_{model}} dmodel倍
5.1 Positional Encoding
Transformer是没有考虑词的顺序(位置)关系的。为了解决这个问题引入位置编码(Positional Encoding),论文中使用的公式如下:
![]()
p o s pos pos表示的是在这句话的第几个位置, i i i表示的是在embedding的第几个维度。所以,通过三角函数,可以计算出这句话的每一个位置的每一个维度的值。
例如输入的ID序列长度为10,那么经过Embeddings层后Tensor的尺寸就是(10,512),此时上式中的pos的范围就是0-9;对于不同维度,这里范围是0-511,偶数维使用sin函数,而奇数维使用cos函数。
这种位置编码的好处是: P E p o s + k PE_{pos+k} PEpos+k可以表示成 P E p o s PE_{pos} PEpos的线性函数,这样网络就能容易的学到相对位置的关系。位置编码的代码如下:
class PositionalEncoding(nn.Module):
"""
Implement the PE function.
"""
def __init__(self, d_model, dropout, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
# Compute the positional encodings once in log space.
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, x):
x = x + self.pe[:, :x.size(1)]
return self.dropout(x)
6.完整模型
这里我们定义一个函数,输入是超参,输出是根据超参构建的模型:
def make_model(src_vocab, tgt_vocab, N=6, d_model=512, d_ff=2048, h=8, dropout=0.1):
"""
Helper: Construct a model from hyperparameters.
"""
c = copy.deepcopy
attn = MultiHeadedAttention(h, d_model)
ff = PositionwiseFeedForward(d_model, d_ff, dropout)
position = PositionalEncoding(d_model, dropout)
model = EncoderDecoder(
Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N),
nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
Generator(d_model, tgt_vocab))
# This was important from their code.
# Initialize parameters with Glorot / fan_avg.
for p in model.parameters():
if p.dim() > 1:
# 初始化
nn.init.xavier_uniform_(p)
return model
四、模型训练
首先我们需要一个Batch类,用于提供批次数据,并且构造所需要的掩码:
class Batch(object):
"""
Object for holding a batch of data with mask during training.
"""
def __init__(self, src, trg=None, pad=0):
self.src = src
self.src_mask = (src != pad).unsqueeze(-2)
if trg is not None:
self.trg = trg[:, :-1]
self.trg_y = trg[:, 1:]
self.trg_mask = self.make_std_mask(self.trg, pad)
self.ntokens = (self.trg_y != pad).sum().item()
@staticmethod
def make_std_mask(tgt, pad):
"""
Create a mask to hide padding and future words.
"""
tgt_mask = (tgt != pad).unsqueeze(-2)
tgt_mask = tgt_mask & subsequent_mask(tgt.size(-1))
return tgt_mask
值得注意的是解码阶段的Mask(代码中是trg_mask)需要将未来时刻的输出掩盖掉,这在前面已经实现了相应的函数(即subsequent_mask函数)。
接下来再写出运行一个epoch的训练代码,非常的简单:
def run_epoch(data_iter, model, loss_compute):
"""
Standard Training and Logging Function
"""
start = time.time()
total_tokens = 0
total_loss = 0
tokens = 0
for i, batch in enumerate(data_iter):
out = model.forward(batch.src, batch.trg, batch.src_mask, batch.trg_mask)
loss = loss_compute(out, batch.trg_y, batch.ntokens)
total_loss += loss
total_tokens += batch.ntokens
tokens += batch.ntokens
if i % 50 == 1:
elapsed = time.time() - start
print("Epoch Step: %d Loss: %f Tokens per Sec: %f" % (i, loss / batch.ntokens, tokens / elapsed))
start = time.time()
tokens = 0
return total_loss / total_tokens
对于优化器(optimizer),论文选用了常见的 Adam optimizer ,相应的优化器参数是 β 1 = 0.9 , β 2 = 0.98 , ϵ = 1 0 − 9 \beta_1=0.9,\beta_2=0.98,\epsilon=10^-9 β1=0.9,β2=0.98,ϵ=10−9。特别的,对于比较重要的学习率参数,是随着训练的进行动态变化的,也就是在最开始的 w a r m u p s t e p s warmup_steps warmupsteps步,学习率线性增加;然后再慢慢的非线性降低。论文中 w a r m u p s t e p s = 4000 warmup_steps=4000 warmupsteps=4000
class NoamOpt(object):
"""
Optim wrapper that implements rate.
"""
def __init__(self, model_size, factor, warmup, optimizer):
self.optimizer = optimizer
self._step = 0
self.warmup = warmup
self.factor = factor
self.model_size = model_size
self._rate = 0
def step(self):
"""
Update parameters and rate.
"""
self._step += 1
rate = self.rate()
for p in self.optimizer.param_groups:
p['lr'] = rate
self._rate = rate
self.optimizer.step()
def rate(self, step=None):
if step is None:
step = self._step
return self.factor * (self.model_size ** (-0.5) * min(step ** (-0.5), step * self.warmup ** (-1.5)))
def get_std_opt(model):
return NoamOpt(model.src_embed[0].d_model, 2, 4000,
torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))
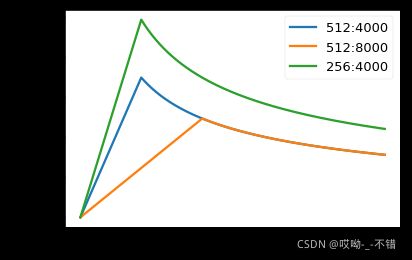
# Three settings of the lrate hyperparameters.
opts = [NoamOpt(512, 1, 4000, None),
NoamOpt(512, 1, 8000, None),
NoamOpt(256, 1, 4000, None)]
plt.plot(np.arange(1, 20000), [[opt.rate(i) for opt in opts] for i in range(1, 20000)])
plt.legend(["512:4000", "512:8000", "256:4000"])
论文中使用到了3种Regularization,一种是Dropout,一种是残差连接,这两种前面已经做出讲解。最后一种是Label Smoothing,虽然Label Smoothing增加了模型训练的困惑度,但是的确使得 accuracy与BLEU上升了,具体实现如下:
class LabelSmoothing(nn.Module):
"""
Implement label smoothing.
"""
def __init__(self, size, padding_idx, smoothing=0.0):
super(LabelSmoothing, self).__init__()
self.criterion = nn.KLDivLoss(reduction='sum')
self.padding_idx = padding_idx
self.confidence = 1.0 - smoothing
self.smoothing = smoothing
self.size = size
self.true_dist = None
def forward(self, x, target):
assert x.size(1) == self.size
true_dist = x.clone()
true_dist.fill_(self.smoothing / (self.size - 2))
true_dist.scatter_(1, target.unsqueeze(1), self.confidence)
true_dist[:, self.padding_idx] = 0
mask = torch.nonzero(target == self.padding_idx)
if mask.size(0) > 0:
true_dist.index_fill_(0, mask.squeeze(), 0.0)
self.true_dist = true_dist
return self.criterion(x, true_dist)
五、Example
论文中要完成的是一个机器翻译任务,但是那可能有点麻烦,所以我们就来完成一个简单的复制任务来检验我们的模型,也就是给定来自一个小型词汇表的token序列,我们的目标是通过Encoder-Decoder结构生成相同的token序列,例如输入是[1,2,3,4,5],那么生成的序列也应该是[1,2,3,4,5]。
任务数据生成代码如下,让src=trg即可。
def data_gen(V, batch, nbatches):
"""
Generate random data for a src-tgt copy task.
"""
for i in range(nbatches):
data = torch.from_numpy(np.random.randint(1, V, size=(batch, 10)))
data[:, 0] = 1
yield Batch(src=data, trg=data, pad=0)
然后是一个计算loss的方法:
class SimpleLossCompute(object):
"""
A simple loss compute and train function.
"""
def __init__(self, generator, criterion, opt=None):
self.generator = generator
self.criterion = criterion
self.opt = opt
def __call__(self, x, y, norm):
x = self.generator(x)
loss = self.criterion(x.contiguous().view(-1, x.size(-1)), y.contiguous().view(-1)) / norm
loss.backward()
if self.opt is not None:
self.opt.step()
self.opt.optimizer.zero_grad()
return loss.item() * norm
在预测阶段是一个自回归模型,为了简单我们直接使用Greedy Search(一般情况下是使用Beam Search),也就是每一个时刻都取概率最大的词作为输出。
def greedy_decode(model, src, src_mask, max_len, start_symbol):
memory = model.encode(src, src_mask)
ys = torch.ones(1, 1, dtype=torch.long).fill_(start_symbol)
for i in range(max_len - 1):
out = model.decode(memory, src_mask, ys, subsequent_mask(ys.size(1)))
prob = model.generator(out[:, -1])
# 选择概率最大的值输出
_, next_word = torch.max(prob, dim=1)
# 得到下一个词
next_word = next_word.item()
# 拼接
ys = torch.cat([ys, torch.ones(1, 1, dtype=torch.long).fill_(next_word)], dim=1)
return ys
最后,将这个例子运行起来,我们便可以看到,几分钟的时间内Transformer已经能够完美的完成这个复制任务!
# Train the simple copy task.
V = 11
# 标签平滑
criterion = LabelSmoothing(size=V, padding_idx=0, smoothing=0.0)
# 构造模型
model = make_model(V, V, N=2)
# 模型优化器
model_opt = NoamOpt(model.src_embed[0].d_model, 1, 400,
torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))
# 训练验证15轮
for epoch in range(15):
model.train()
run_epoch(data_gen(V, 30, 20), model, SimpleLossCompute(model.generator, criterion, model_opt))
model.eval()
print(run_epoch(data_gen(V, 30, 5), model, SimpleLossCompute(model.generator, criterion, None)))
# This code predicts a translation using greedy decoding for simplicity.
print()
print("{}predict{}".format('*' * 10, '*' * 10))
# 预测
model.eval()
src = torch.tensor([[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]])
src_mask = torch.ones(1, 1, 10)
print(greedy_decode(model, src, src_mask, max_len=10, start_symbol=1))
Epoch Step: 1 Loss: 3.023465 Tokens per Sec: 403.074173
Epoch Step: 1 Loss: 1.920030 Tokens per Sec: 641.689380
1.9274832487106324
Epoch Step: 1 Loss: 1.940011 Tokens per Sec: 432.003378
Epoch Step: 1 Loss: 1.699767 Tokens per Sec: 641.979665
1.657595729827881
Epoch Step: 1 Loss: 1.860276 Tokens per Sec: 433.320240
Epoch Step: 1 Loss: 1.546011 Tokens per Sec: 640.537198
1.4888023376464843
Epoch Step: 1 Loss: 1.682198 Tokens per Sec: 432.092305
Epoch Step: 1 Loss: 1.313169 Tokens per Sec: 639.441857
1.3485562801361084
Epoch Step: 1 Loss: 1.278768 Tokens per Sec: 433.568756
Epoch Step: 1 Loss: 1.062384 Tokens per Sec: 642.542067
0.9853351473808288
Epoch Step: 1 Loss: 1.269471 Tokens per Sec: 433.388727
Epoch Step: 1 Loss: 0.590709 Tokens per Sec: 642.862135
0.5686767101287842
Epoch Step: 1 Loss: 0.997076 Tokens per Sec: 433.009746
Epoch Step: 1 Loss: 0.343118 Tokens per Sec: 642.288427
0.34273059368133546
Epoch Step: 1 Loss: 0.459483 Tokens per Sec: 434.594030
Epoch Step: 1 Loss: 0.290385 Tokens per Sec: 642.519464
0.2612409472465515
Epoch Step: 1 Loss: 1.031042 Tokens per Sec: 434.557008
Epoch Step: 1 Loss: 0.437069 Tokens per Sec: 643.630322
0.4323212027549744
Epoch Step: 1 Loss: 0.617165 Tokens per Sec: 436.652626
Epoch Step: 1 Loss: 0.258793 Tokens per Sec: 644.372296
0.27331129014492034
参考
- The Annotated Transformer
- Transformer代码实现
如果对您有帮助,麻烦点赞关注,这真的对我很重要!!!如果需要互关,请评论或者私信!
![]()