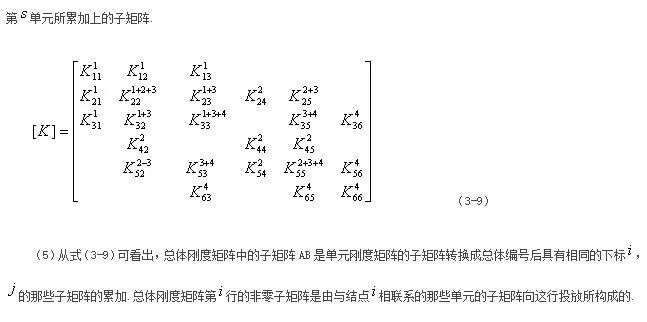
python symbols函数_有限元平面四边形等差单元python编程
Part I : 平面四边形等差单元理论部分:
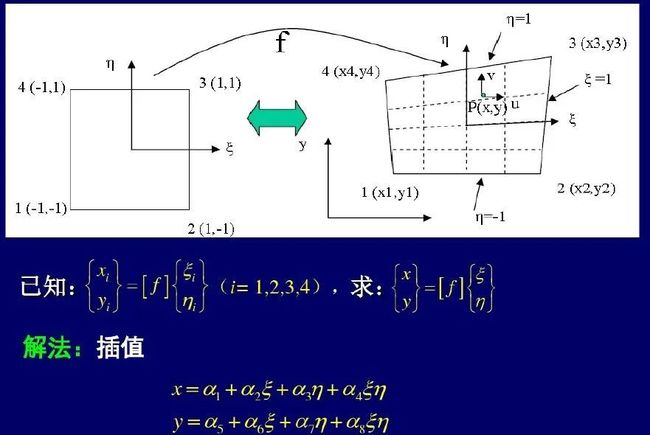
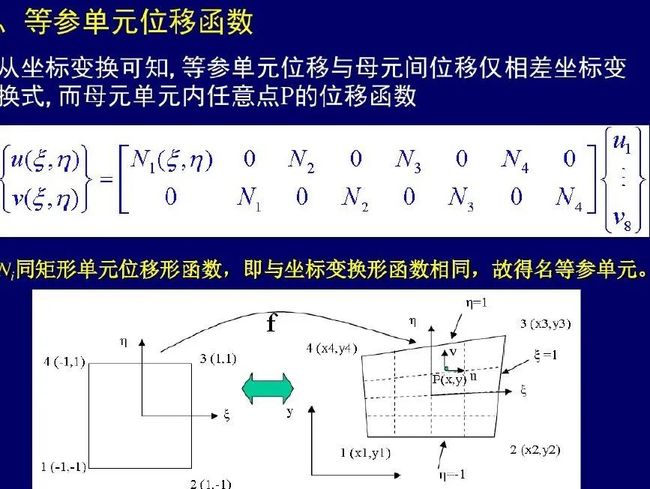
平面四边形等差单元 是由矩形单元 作等参变换(坐标映射)而来。
四边形等参单元的刚度矩阵是二重积分式,我想用Maple求解析解,算了很久也没有算出结果。所有我的编程思路是先用 sympy 求出 单元刚度矩阵的符号解,再用lambdify函数将符号解的单元刚度矩阵的各元素转为普通的python函数,最后用scipy进行二重数值积分。Part II : 四边形等参单元的刚度矩阵的python代码:
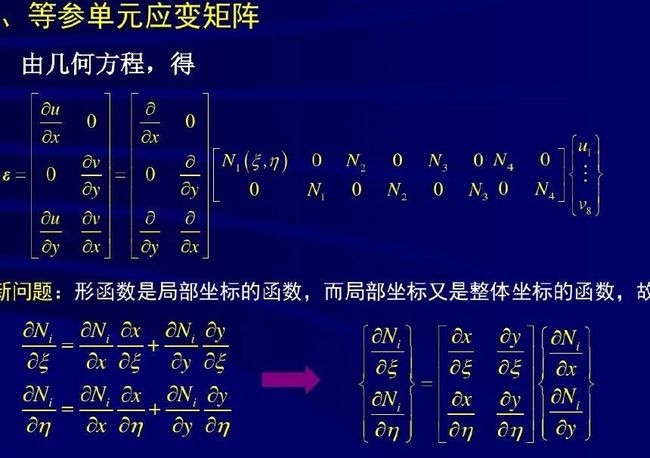
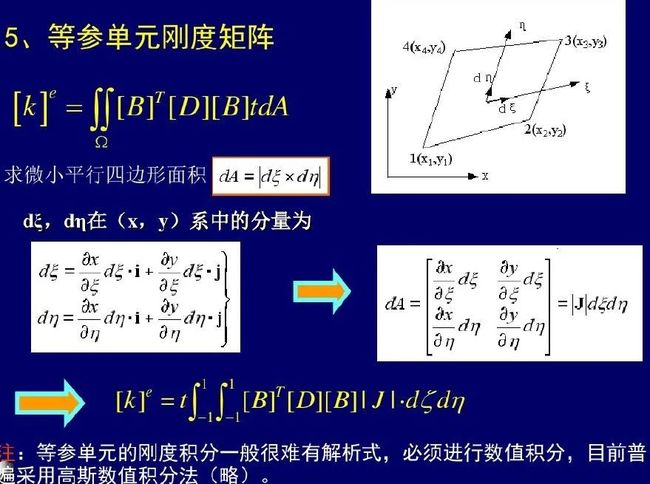
import numpy as npfrom scipy.integrate import dblquadfrom sympy import symbols, Matrix, diff,simplifyfrom sympy.utilities.lambdify import lambdifyclass Quad8():# 四边形平面应力单元,4个节点,8个自由度 def __init__(self,nodes,t=1,E=20000, nu=0.25): self.nodes = nodes self.x1 = self.nodes[0,0] self.x2 = self.nodes[1,0] self.x3 = self.nodes[2,0] self.x4 = self.nodes[3,0] self.y1 = self.nodes[0,1] self.y2 = self.nodes[1,1] self.y3 = self.nodes[2,1] self.y4 = self.nodes[3,1] self.t = t self.E = E self.nu = nu #定义积分变量 self.xi = symbols("xi") self.eta = symbols("eta") self.calculate_shapeFunc() self.calculate_abcd() self.calculate_J() self.calculate_B() self.calculate_D() self.calculate_Ke() def calculate_shapeFunc(self):#四边形单元形函数 self.N1 = 0.25* (1 - self.xi)*(1 - self.eta) self.N2 = 0.25* (1 + self.xi)*(1 - self.eta) self.N3 = 0.25* (1 + self.xi)*(1 + self.eta) self.N4 = 0.25* (1 - self.xi)*(1 + self.eta) def calculate_abcd(self):#系数 self.a = 0.25* (self.y1*(self.xi-1)-self.y2*(1+self.xi)+self.y3*(1+self.xi)-self.y4*(self.xi-1)) self.b = 0.25* (self.y1*(self.eta-1)+self.y2*(1-self.eta)+self.y3*(1+self.eta)-self.y4*(1+self.eta)) self.c = 0.25* (self.x1*(self.eta-1)-self.x2*(self.eta-1)+self.x3*(1+self.eta)-self.x4*(1+self.eta)) self.d = 0.25* (self.x1*(self.xi-1)-self.x2*(1+self.xi)+self.x3*(1+self.xi)-self.x4*(self.xi-1)) def calculate_J(self): #单元雅各比矩阵行列式 X = Matrix(self.nodes[:,0].reshape((1,-1))) # 1x4 Y = Matrix(self.nodes[:,1]) # 4x1 # M 4x4 M = Matrix([[0, 1-self.eta, self.eta-self.xi, self.xi-1], [self.eta-1, 0, 1+self.xi, -self.xi-self.eta], [self.xi-self.eta, -self.xi-1, 0, 1+self.eta], [1-self.xi, self.xi+self.eta, -1-self.eta, 0]]) self.J = 0.125* X* M * Y # 1行1列 self.J = self.J[0,0] #print(self.J) #print(1.0/ self.J) def calculate_B(self): #单元应变矩阵,需要用到符号变量微分 self.B = Matrix(np.zeros((3,8))) self.B[0,0] = self.a*(diff(self.N1, self.xi))-self.b*(diff(self.N1, self.eta)) self.B[1,1] = self.c*(diff(self.N1, self.eta))-self.d*(diff(self.N1, self.xi)) self.B[2,0] = self.c*(diff(self.N1, self.eta))-self.d*(diff(self.N1, self.xi)) self.B[2,1] = self.a*(diff(self.N1, self.xi))-self.b*(diff(self.N1, self.eta)) self.B[0,2] = self.a*(diff(self.N2, self.xi))-self.b*(diff(self.N2, self.eta)) self.B[1,3] = self.c*(diff(self.N2, self.eta))-self.d*(diff(self.N2, self.xi)) self.B[2,2] = self.c*(diff(self.N2, self.eta))-self.d*(diff(self.N2, self.xi)) self.B[2,3] = self.a*(diff(self.N2, self.xi))-self.b*(diff(self.N2, self.eta)) self.B[0,4] = self.a*(diff(self.N3, self.xi))-self.b*(diff(self.N3, self.eta)) self.B[1,5] = self.c*(diff(self.N3, self.eta))-self.d*(diff(self.N3, self.xi)) self.B[2,4] = self.c*(diff(self.N3, self.eta))-self.d*(diff(self.N3, self.xi)) self.B[2,5] = self.a*(diff(self.N3, self.xi))-self.b*(diff(self.N3, self.eta)) self.B[0,6] = self.a*(diff(self.N4, self.xi))-self.b*(diff(self.N4, self.eta)) self.B[1,7] = self.c*(diff(self.N4, self.eta))-self.d*(diff(self.N4, self.xi)) self.B[2,6] = self.c*(diff(self.N4, self.eta))-self.d*(diff(self.N4, self.xi)) self.B[2,7] = self.a*(diff(self.N4, self.xi))-self.b*(diff(self.N4, self.eta)) self.B *= 1.0/self.J #print(self. B) def calculate_D(self): #平面应力单元弹性矩阵 self.D = np.mat([[1, self.nu, 0], [self.nu, 1, 0], [0, 0, 0.5*(1-self.nu)]]) self.D *= self.E/(1-self.nu*self.nu) # 对于平面应变为题,只需将E换成 E/(1-nu**2),nu 换成 nu/(1-nu) def calculate_Ke(self): #单元刚度矩阵Ke, Ke 为对称方阵 Z = self.J* self.B.T * self.D * self.B self.Ke = np.zeros((8,8)) # Z.shape 8x8 (单元自由度x单元自由度) for i in range(8): #利用刚度矩阵的对称性,先只计算下三角 for j in range(i+1): # xi 和 eta 从-1到1 二重积分,再乘以厚度 #func =lambdify((self.xi,self.eta),simplify(Z[i,j]),modules='numpy') func =lambdify((self.xi,self.eta),Z[i,j],modules='numpy') ok = self.t * dblquad(func,-1,1,-1,1,epsabs=1.49e-08, epsrel=1.49e-08)[0] self.Ke[i,j] = ok self.Ke[j,i] = ok #上三角 镜像得到 #后处理计算 def calculate_Strain(self,disp_elem,loc =4): #loc 取值0,1,2,3和4,分别代表4个节点和单元中心(loc=4) #计算应变,单元应变不是常数,是双线性差值,跟位置有关 self.Strain = np.zeros((3,1)) SS = self.B * disp_elem #是xi和eta的函数 dic = {0:(-1,-1),1:(1,-1),2:(1,1),3:(-1,1),4:(0,0)} for i in range(3): self.Strain[i,0] = SS[i,0].subs({self.xi:dic[loc][0], self.eta:dic[loc][1]}) #单元中心的应变 def calculate_Stress(self): self.Stress = self.D * self.Strain def calculate_Strain_4N(self,disp_elem): #4个节点全部计算出来 #计算应变,单元应变不是常数,是双线性差值,跟位置有关 self.Strain_4N = np.zeros((4,3,1)) SS = self.B * disp_elem #是xi和eta的函数 dic = {0:(-1,-1),1:(1,-1),2:(1,1),3:(-1,1),4:(0,0)} for n in range(4): for i in range(3): self.Strain_4N[n,i,0] = SS[i,0].subs({self.xi:dic[n][0], self.eta:dic[n][1]}) #单元中心的应变 def calculate_Stress_4N(self):#4个节点全部计算出来 self.Stress_4N = np.zeros((4,3,1)) for n in range(4): self.Stress_4N[n] = self.D * self.Strain_4N[n]Part III : 刚度矩阵的组装,以及载荷和约束的处理 的理论基础
Part IV : 刚度矩阵的组装、位移,应变,应力求解的python代码
from numpy import array, mat,zeros, double, integer,float64,sqrtfrom numpy.linalg import solve #,detfrom random import randomfrom Quad8 import Quad8from readFromFemap_quad import readNeuFileimport timetime1 = time.time()#单位体系 N,mm, ton#目前没有想好网格生成的算法,节点坐标和单元的拓扑信息暂由有限元前处理软件导出后由python读入#Nodes info.: x,y,z. #Node Id must start from 1,the step is 1.#读入节点坐标和单元信息 #节点无编号,由0自增。NODE, ELEM = readNeuFile("T1.neu")NODE = array(NODE,dtype=double)ELEM = array(ELEM,dtype=integer)'''NODE= array([[0,0,0], [250,0,0], [250,250,0], [0,250,0], [500,0,0], [500,250,0]], dtype=double)'''#Node ID 从0开始,步长1为1自增node_qty = NODE.shape[0] #节点数量#MAT ID,TYPE ID,4 Nodes' ID'''ELEM = array([[1,1,0,1,2,3], [1,1,1,4,5,2]], dtype=integer)#单元ID 从0开始,步长1为1自增'''elem_qty = ELEM.shape[0] #单元数量#Boundary conditions#节点自由度 dof CONSTRAINtrain#node id, dof id(0 for x, 1 for y...),displacement of the dof idCONSTRAIN=array([[0,0,0.0], [0,1,0.0], [22,0,0.0], [22,1,0.0], [23,0,0.0], [23,1,0.0], [24,0,0.0], [24,1,0.0], [25,0,0.0], [25,1,0.0] ])#外力 Force矩阵F = mat(zeros((node_qty*2,1)), dtype=double)F[2*47]= -5000 # Fx on node 47F[2*59]= -5000 # Fx on node 59#F[2*5+1]= 9750 # Fy on node 5#材料属性E=70326.6 # 弹性模量 #铝2080nuxy = 0.33 #泊松比t = 2.0 #薄板厚度time2 = time.time()print(f"有限元模型输入完成!耗时{time2-time1}")有限元边界条件如下(代码中的节点ID 从0开始,是图中的数字减去1后的结果):
左边的5个单元x和y向位移均为0。锤子角两个节点y向载荷 -5000N。
def assembleK(NODE,ELEM,CONSTRAIN): elems = [] #用于存储单元对象 K= mat(zeros((node_qty*2,node_qty*2)), dtype=float64)#初始化总刚度矩阵 #遍历单元 for ie in range(elem_qty): i,j,m,n = ELEM[ie,2:2+4] #单元的4个节点的ID: xi=NODE[i,0] yi=NODE[i,1] xj=NODE[j,0] yj=NODE[j,1] xm=NODE[m,0] ym=NODE[m,1] xn=NODE[n,0] yn=NODE[n,1] #X[:,ie ] = mat([[xi], [xj], [xm],[xn]])#X坐标#用于后处理 #Y[:,ie ] = mat([[yi], [yj], [ym],[yn]])#Y坐标#用于后处理 nodes = array([[xi,yi],[xj,yj],[xm,ym],[xn,yn]]) elem = Quad8(nodes,t=t,E=E,nu=nuxy)#生成单元 elems.append(elem) Ke = elem.Ke #单元刚度矩阵Ke=[Kii,Kij,Kim,Kin; # Kji,Kjj,Kjm,Kjn; # Kmi,Kmj,Kmm,Kmn; # Kni,Knj,Knm,Knn] #总刚度矩阵组装(更新4x4个区域) K[2*i : 2*i+2 ,2*i :2*i+2] += Ke[0:2,0:2] K[2*i : 2*i+2, 2*j :2*j+2] += Ke[0:2,2:4] K[2*i : 2*i+2, 2*m: 2*m+2] += Ke[0:2,4:6] K[2*i : 2*i+2, 2*n: 2*n+2] += Ke[0:2,6:8] K[2*j :2*j+2, 2*i: 2*i+2] += Ke[2:4,0:2] K[2*j :2*j+2, 2*j: 2*j+2] += Ke[2:4,2:4] K[2*j: 2*j+2, 2*m: 2*m+2] += Ke[2:4,4:6] K[2*j: 2*j+2, 2*n: 2*n+2] += Ke[2:4,6:8] K[2*m: 2*m+2, 2*i: 2*i+2] += Ke[4:6,0:2] K[2*m: 2*m+2, 2*j: 2*j+2] += Ke[4:6,2:4] K[2*m: 2*m+2, 2*m: 2*m+2] += Ke[4:6,4:6] K[2*m: 2*m+2, 2*n: 2*n+2] += Ke[4:6,6:8] K[2*n: 2*n+2, 2*i: 2*i+2] += Ke[6:8,0:2] K[2*n: 2*n+2, 2*j: 2*j+2] += Ke[6:8,2:4] K[2*n: 2*n+2, 2*m: 2*m+2] += Ke[6:8,4:6] K[2*n: 2*n+2, 2*n: 2*n+2] += Ke[6:8,6:8] #将边界条件(力,位移约束)更新到刚度矩阵;更新外力矩阵 BigNum = 1.0e150#大数法 cr = CONSTRAIN.shape[0] #遍历约束节点 for ic in range(CONSTRAIN.shape[0]): jj = 2* CONSTRAIN[ic,0] + CONSTRAIN[ic,1] # 约束在总刚度矩阵的行号 jj = int(jj)#CONSTRAIN 是浮点型数组,所有jj的结果是浮点型。做索引需是整数 K[jj, jj] *= BigNum #总刚度矩阵对角线上的元素乘以大数 F[jj] = K[jj, jj]*CONSTRAIN[ic, 2] #载荷也用更新后的K[jj,jj]乘以指定位移 return K, elems # SOLVE# 求解 位移矩阵Deformation Matrix DISPK,elems = assembleK(NODE,ELEM,CONSTRAIN)time3 = time.time()print(f"总刚度矩阵组装完成!耗时{time3-time2}")DISP= solve(K, F)#位移矩阵#将位移在边界条件节点上的值用输入的约束值修正for ic in range(CONSTRAIN.shape[0]): jj = 2* CONSTRAIN[ic,0] + CONSTRAIN[ic,1] jj=int(jj) DISP[jj] = CONSTRAIN[ic,2]time4 = time.time()print(f"位移矩阵求解完成!耗时{time4-time3}")#print("位移矩阵:")#print(DISP)#之前位移矩阵内数的排列次序是节点1 x向位移,节点1 y向位移; 节点2....#提高可读性:现在每个节点Ux,Uy 显示在同一行Delta = DISP.reshape((-1,2))X= NODE[:,0]Y= NODE[:,1]Delta_X = array(Delta[:,0])Delta_Y = array(Delta[:,1])#节点总位移DISP_total = sqrt(Delta_X**2 + Delta_Y**2)#遍历单元,求各个单元上各个节点上的应力和应变for ie in range(elem_qty): i,j,m,n = ELEM[ie,2:2+4] #单元的4个节点的ID: DISPe = mat([[DISP[2*i,0]], [DISP[2*i+1,0]], [DISP[2*j,0]], [DISP[2*j+1,0]], [DISP[2*m,0]], [DISP[2*m+1,0]], [DISP[2*n,0]], [DISP[2*n+1,0]]]) #print(DISPe) elem = elems[ie] #当前计算的单元 #loc = 4 #loc 取值0,1,2,3和4,分别代表单元的4个节点和单元中心(loc=4) elem.calculate_Strain_4N(DISPe) elem.calculate_Stress_4N() #print(f"单元{ie}在loc={loc}处的应力矩阵:") #print(elem.Stress)#找出每个节点对应的多(或1)个单元及在这些单元上的位置def find_elem_locaton(node_qty,ELEM): elem_loc_List=[] # [[(elemID,locID),...],...] for i in range(node_qty):#遍历节点 elem_loc_list = [] for j in range(elem_qty): for k in range(4): if ELEM[j, k+2] == i: elem_loc_list.append((j, k)) #print(f"在 element{j},location {k} 找到 node{i}") break elem_loc_List.append(elem_loc_list) return elem_loc_Listelem_loc_List = find_elem_locaton(node_qty,ELEM)# 节点的单元平均应变(在节点所在的各单元平均NodeMeanStain = zeros((node_qty, 3+1, 1),dtype = float64)#加上Z向正应变# 节点的单元平均应力(在节点所在的各单元平均NodeMeanStress = zeros((node_qty, 3, 1),dtype = float64)for i in range(node_qty): n = len(elem_loc_List[i]) StrainSum = zeros((3, 1),dtype = float64) StressSum = zeros((3, 1),dtype = float64) for j in range(n): elemID,loc = elem_loc_List[i][j] elem = elems[elemID] StrainSum += elem.Strain_4N[loc] StressSum += elem.Stress_4N[loc] NodeMeanStain[i,0:3] = StrainSum /n NodeMeanStress[i] = StressSum /n NodeMeanStain[i,3] = -nuxy/E*(NodeMeanStress[i,0]+NodeMeanStress[i,1]) meanMajorPrnStress = 0.5*(NodeMeanStress[:,0] +NodeMeanStress[:,1])+sqrt((0.5*(NodeMeanStress[:,0] -NodeMeanStress[:,1]))**2 + NodeMeanStress[:,2]**2) #主应力1meanMinorPrnStress = 0.5*(NodeMeanStress[:,0] +NodeMeanStress[:,1])-sqrt((0.5*(NodeMeanStress[:,0] -NodeMeanStress[:,1]))**2 + NodeMeanStress[:,2]**2) #主应力2(次)meanVonmiStress = sqrt(0.5*((meanMajorPrnStress-meanMinorPrnStress)**2 + meanMajorPrnStress**2 + meanMinorPrnStress**2)) # 冯米塞斯应力 Von mises stress#for i in range(node_qty): #print(f"节点{i}的单元平均应变矩阵:") #print(NodeMeanStain[i])#for i in range(node_qty): #print(f"节点{i}的单元平均应力矩阵:") #print(NodeMeanStress[i])#结果可视化#from numpy import array,zeros,integerimport sysfrom PyQt5.QtCore import *from PyQt5.QtGui import *from PyQt5.QtWidgets import *from PyQt5.QtOpenGL import QGLWidgetfrom OpenGL import GL# 后处理'''K*X = F 求解出来的 位移矩阵是 按节点排列的。size 2*node_qty x 1。应变和应力的求解是在单元中进行的应变和应力 在各节处的取值(平均值 or最大值)又需要在 共享该节点的各单元上 取平均 或者取最大值结果云图绘制又是按单元进行的所以数据需要按 节点->单元 -> 节点 - > 单元 进行转化。'''def nodeData2ElemData(nodeData, ELEM, nodes_per_elem =4): '''后处理云图是按照单元依次绘制,所有须要把按节点排列的数据转化为按单元排列''' node_qty = nodeData.shape[0] # 按节点排序的 X向应力 等等这样的数组,size node_qty x 1 elem_qty = ELEM.shape[0] # ELEM 中 2到5 列包含单元中4个节点的ID elemData = zeros((elem_qty,nodes_per_elem),dtype =nodeData.dtype) for i in range(elem_qty): for j in range(nodes_per_elem): nodeID = ELEM[i,2+j] #须为整数 # ELEM 中 2到5 列包含单元中4个节点的ID elemData[i,j] = nodeData[nodeID] return elemDatadef scaleXY(X,Y,k =2):# 输出用于OPENGL 绘图的坐标 # 传入按单元排列的坐标数据。 X and Y size :elem_qty x nodes_per_elem max_X, min_X = X.max(), X.min() max_Y, min_Y = Y.max(), Y.min() max_span = max(max_X-min_X,max_Y-min_Y) X_scaled = (X- min_X)/ max_span*k -1 Y_scaled = (Y- min_Y)/ max_span*k -k/4.0 return X_scaled, Y_scaledX= nodeData2ElemData(X,ELEM)Y= nodeData2ElemData(Y,ELEM)Delta_X = nodeData2ElemData(Delta_X,ELEM)Delta_Y = nodeData2ElemData(Delta_Y,ELEM)scale =5X_new = X + scale* Delta_XY_new = Y + scale* Delta_YX, Y = scaleXY(X,Y) # 用于绘图的变形前的缩放后的坐标X_new_scaled, Y_new_scaled = scaleXY(X_new,Y_new) # 用于绘图的变形后的缩放后的坐标#计算按单元排列的各个后处理变量DISP_total = nodeData2ElemData(DISP_total,ELEM) #总位移meanXStrain = nodeData2ElemData(NodeMeanStain[:,0],ELEM)# X向正应变meanYStrain = nodeData2ElemData(NodeMeanStain[:,1],ELEM)# Y向正应变meanXYSrain = nodeData2ElemData(NodeMeanStain[:,2],ELEM)# XY剪应变meanZStrain = nodeData2ElemData(NodeMeanStain[:,3],ELEM)# Z向正应变meanXStress = nodeData2ElemData(NodeMeanStress[:,0],ELEM)# X向正应力meanYStress = nodeData2ElemData(NodeMeanStress[:,1],ELEM)# Y向正应力meanXYStress = nodeData2ElemData(NodeMeanStress[:,2],ELEM)# XY剪应力meanMajorPrnStress = nodeData2ElemData(meanMajorPrnStress,ELEM)# X向正应力 #主应力1meanMinorPrnStress = nodeData2ElemData(meanMinorPrnStress,ELEM)# X向正应力 #主应力1meanVonmiStress = nodeData2ElemData(meanVonmiStress,ELEM) # 冯米塞斯应力Part V : 有限元后处理数据的云图绘制
(OPENGL绘图,这部分不是本篇的重点)
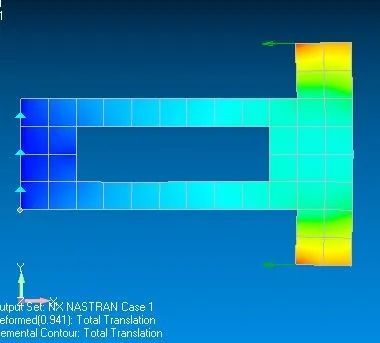
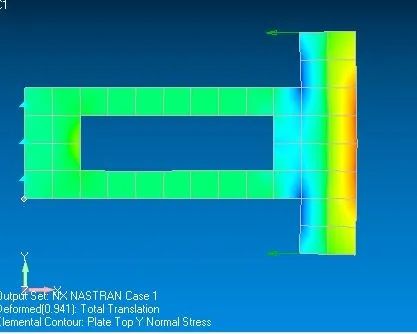
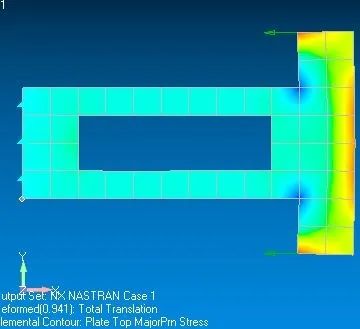
#云图显示class GLWidget(QGLWidget): def __init__(self, parent =None): super(GLWidget, self).__init__(parent) def initializeGL(self): self.qglClearColor(QColor("black")) #背景色 GL.glShadeModel(GL.GL_SMOOTH) #!颜色平滑渲染 self.object = self.makeObject( Delta_X, X_new_scaled,Y_new_scaled)#2020.9.19 def paintGL(self): GL.glClear(GL.GL_COLOR_BUFFER_BIT | GL.GL_DEPTH_BUFFER_BIT) GL.glLoadIdentity()# Reset The Projection Matrix GL.glCallList(self.object) def resizeGL(self, width, height): side = min(width, height) GL.glViewport((width - side) // 2, (height - side) // 2, side, side)#保持图形的长宽比 #GL.glViewport(50,50,500,500) GL.glMatrixMode(GL.GL_PROJECTION) GL.glLoadIdentity()# Reset The Projection Matrix #GL.glOrtho(-0.5, +0.5, +0.5, -0.5, 4.0, 15.0) GL.glMatrixMode(GL.GL_MODELVIEW) def makeObject(self,elemData,X,Y): genList = GL.glGenLists(1) GL.glNewList(genList, GL.GL_COMPILE) LSL= elemData.min() USL= elemData.max() print(f"当前数据集最大值:{USL}, 最小值: {LSL}") for i in range(elem_qty): #GL.glBegin(GL.GL_POLYGON)# 开始绘制多边形 GL.glBegin(GL.GL_QUADS)# 开始绘制四边形 for j in range(4): #四节点单元!!! if LSL==USL: r,g,b = (0,1,0) else: r,g,b = self.num2RGB(elemData[i,j],LSL,USL) GL.glColor3f(r,g,b) x,y = X[i,j], Y[i,j] GL.glVertex2f(x,y) GL.glEnd() GL.glLineWidth(1.0) GL.glBegin(GL.GL_LINE_LOOP)#画线 GL.glColor3f(1,1,1) GL.glVertex2f(X[i,0],Y[i,0]) GL.glVertex2f(X[i,1],Y[i,1]) GL.glVertex2f(X[i,2],Y[i,2]) GL.glVertex2f(X[i,3],Y[i,3]) GL.glEnd() GL.glEndList() return genList def num2RGB(self,x,LSL=0, USL=1.0): r=(x-LSL)/(USL-LSL) if r>=0.75: return (1, 1*(1-r)*4, 0) elif r>=0.5: return (1*(r-0.5)*4, 1, 0) elif r>=0.25: return (0, 1, 1*(0.5-r)*4) elif r>=0: return (0, 1*r*4, 1) def minimumSizeHint(self): return QSize(100, 100) class MainWindow(QMainWindow): def __init__(self): super().__init__() self.setCentralWidget(GLWidget()) global scale self.setWindowTitle("X") self.resize(1000, 700)app = QApplication(sys.argv)mainWin = MainWindow()mainWin.show()sys.exit(app.exec_()) Part VI : 云图展示(我的结果和由Nastran计算得到的结果做对比)
总位移:
X向正应力:
Y向正应力:
第一主应力:
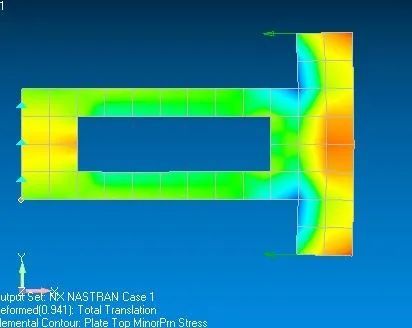
第二主应力:
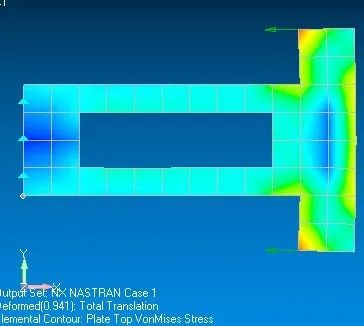
Vonmises 应力: