图像处理 基础知识
前言
每天想你的时候,天上就飘落一粒沙,从此成了撒哈拉。
从枯燥的生活中找到乐趣与幸福,觉得三毛的《撒哈拉沙漠的故事》亲临了生活的真谛。
感觉就是赶鸭子上架╮(╯▽╰)╭,小日子真的有点忙。暑假实习完被学校强制从上海拉了回来广东,强制要求到广州生产实习,愣是在广州学了一个月的大数据。虽然大数据真的挺好玩的,但是好像学的是数据搬运工的方向( ⊙ o ⊙ )啊!。
一个月后,回来了学校,开的课程居然是图像处理和数学建模。整本书翻开都是数学公式……内心崩溃!!!
O(∩_∩)O哈哈~
基础概念
图像
照片、图片、景物、文字等等可以转换为视觉信息的东西。“One picture is worth more than ten thousand words.”
图像的特点:直观形象、易懂、信息量大。
连续图像
一般情况下,我们感兴趣的多数图像都是由“照射源”和形成图像的“场景元素”对光能的反射或者吸收而产生的,是连续的模拟图像,其幅值与坐标都是连续的。
数字图像
将一副二维的连续图像通过有限个离散点来表示就成了数字图像,该过程即为数字图像的采集。其中每个点称为图像元素,即像素。
图像采集
成像系统所产生的图像是由一系列的模拟信号所组成的,这些模拟信号的幅值与空间坐标都是连续的。为了产生数字图像,需要将连续的模拟信号转化为数字形式,即图像采集。图像采集包括两种处理:采样和量化。
图像类型
| 图像类型 | 分类 | 说明 |
|---|---|---|
| 按灰度分类 | 二值图像 | 每个像素只有黑色和白色之分,其数值只能是0或者1,0表示黑、1表示白。 |
| 灰度图片 | 每个像素的亮度采用一个数值(8bit)来表示,通常数值范围在0到255之间,0表示黑、255表示白,其它值表示处于黑白之间。 | |
| 按运动分类 | 静态图像 | 包括静止图像和凝固图像(动态图像中的一帧)。 |
| 动态图像 | 由一组静态图像按照时间的先后顺序排列而成。 | |
| 按色彩分类 | 单色图像 | 某一谱端的灰度图。 |
| 彩色图像 | 彩色图像的像素可以用红绿蓝三元组来表示。通常,三元组的每个数值也是在0到255之间,0表示响应的基色在该像素中没有,而255则代表相应的基色在该像素中取得最大值。 |
分辨率
空间分辨率
空间分辨率指的是图像中可辨别的最小细节。
空间分辨率是由采样过程(采样间隔)决定的。一般来说,采样间隔越大,所得图像像素数越少,空间分辨率低,质量差,严重时出现马赛克效应;采样间隔越小,所得图像像素数越多,空间分辨率高,图像质量好,但数据量大。
灰度分辨率
灰度分辨率是指在灰度级别中可分辨的最小变化。灰度级分辨率是由量化过程决定的。通常把大小为 M × N M×N M×N、灰度为 L L L级的数字图像称为空间分辨率为 M × N M×N M×N,灰度级分辨率为 L L L级的数字图像。
对比度
对比度是指一幅图像中灰度反差的大小, 对 比 度 = 最 大 亮 度 / 最 小 亮 度 对比度= 最大亮度 / 最小亮度 对比度=最大亮度/最小亮度。
清晰度
与清晰度有光的主要因素:
- 亮度
- 对比度
- 尺寸大小
- 细微层次
- 颜色饱和度
图像工程
摘录自:图像工程的三个层次
- 图像技术近年来得到了极大的重视和长足的进展,出现了许多新理论、新方法、新算法、新手段、新设备。图像界一致认为亟需对他们进行研究和集成应用,而这个工作需要在一个整体框架下进行,这个框架就是图像工程。
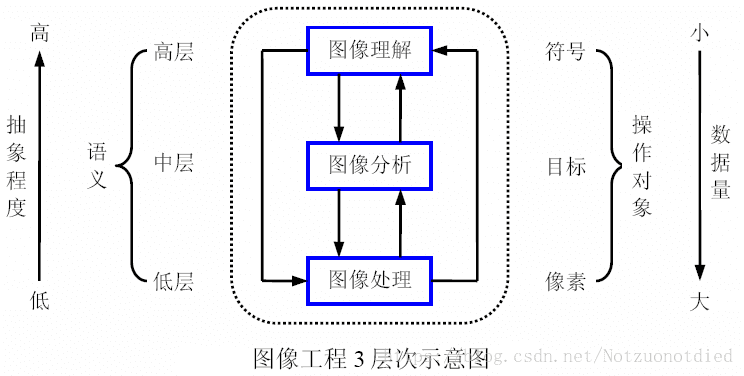
- 图像工程的内容非常丰富。根据抽象程度和研究方法等的不同可分为三个层次:图像处理、图像分析和图像理解。
图像工程的三个层次
- 图像处理着重强调图像到图像之间进行的变换。对图像进行各种加工以改善图像的视觉效果并为自动识别打基础,或对图像进行压缩编码以减少对其所需存储空间或传输时间的要求。
- 图像分析是对图像中感兴趣的目标进行检测和测量,以获得它们的客观信息从而建立对图像的描述。图像分析是一个从图像到数据的过程,这里数据可以是对目标特征检测的结果或是基于测量的符号表示。
- 图像理解的重点是在图像分析的基础上,借助知识、经验等进一步研究图像中各目标的性质和他们之间的相互联系,并得出对图像内容含义的理解以及对原来客观场景的解释,从而指导和规划行动。
- 低层处理:图像处理,也称图像预处理;
- 高层处理:称为图像识别、图像理解或计算机视觉,属于人工智能领域。
图像处理的基本内容
| 基本内容 | 说明 |
|---|---|
| 图像获取 | 将模拟图像装换成适合计算机或者数字设备的数字信号。 |
| 图像变换 | 对图像执行某种正交变换,如离散傅里叶变换、离散余弦变换、沃尔什变换、哈达玛变换、霍特林变换等。 |
| 图像增强 | 突出图像中感兴趣的信息,衰减或去除不需要的信息,从而使有用的信息得到增强,便于目标区分或者对象解释。图像增强的主要方法有直方图增强、空域增强、频域增强、伪彩色增强等技术。 |
| 图像复原 | 去除噪声干扰和消除模糊,恢复图像本来面目。图像噪声包括随机噪声和相干噪声。随机噪声包含了麻点干扰,相干噪声干扰表现为网纹干扰。模糊来自透镜散焦、相对运动、大气湍流以及云层的遮挡等。这些干扰可以用逆滤波、维纳滤波、约束最小二乘方滤波、同态滤波等方法加以去除。 |
| 图像编码 | 利用图像信号的统计特性以及人类视觉的生理学及心理学特性对图像信号进行高效压缩从而减少数据存储量,降低数据率以减小传输带宽,压缩信息量以便于图像分析和识别。图像编码的主要方法有冗余编码、变换编码、小波变换编码、神经网络编码、模型基编码等。 |
| 图像分析 | 对图像中感兴趣的目标进行检测和测量,以获得所需的客观信息。利用边缘检测、区域分割、特征抽取等手段将原来以像素描述的图像变成比较简洁的对目标的描述。 |
| 图像识别 | 大致分为:统计识别法、句法(结构)识别法和模糊识别法。统计识别法侧重于图像的特征,可以用贝叶斯分类器、人工神经网络、支持向量机来实现;句法识别法侧重于图像模式的结构,可以通过句法分析或者对应的自动机来实现;模糊识别法主要是将模糊数学方法引入图像识别,从而简化识别系统的结构,提高系统的实用性和可靠性、更深入的模拟人脑认识事物的模糊性。 |
| 图像理解 | 得出图像内容的理解以及对对原来客观场景的解释。 |
像素间的联系
概念
| 像素邻接 | 像素连接 |
|---|---|
| 两个像素是否连接 | 邻接仅考虑像素间的空间关系,即两个像素在空间上若相互接触,则认为它们两者为邻接的。 |
| 两个像素是否连接 | 1. 在空间上是否邻接; 2.它们的灰度值是否满足某个特定的相似准则(例如,同在一个灰度值集合中取值) |
像素的邻域
| 邻域 | 说明 |
|---|---|
| 4-邻域 N 4 ( p ) N_4(p) N4(p) | 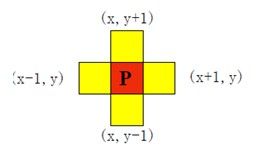 |
| 对角领域 N D ( p ) N_D(p) ND(p) | 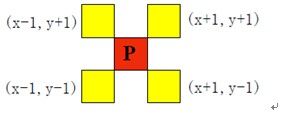 |
| 8-邻域 N 8 ( p ) N_8(p) N8(p) |  |
连通性
- 连通性是描述区域和边界的重要概念,两个像素连通的两个必要条件是:两个像素的位置是否相邻,两个像素的灰度值是否满足特定的相似性准则(或者是否相等)。
像素的连通
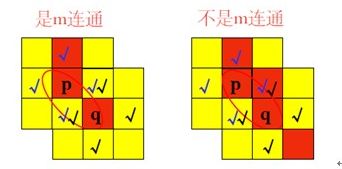
若两个像素具有相同性质,且能够找到两两连接的一条通路——则称它们是连通的。
- 通路由一系列依次连接的像素组成:
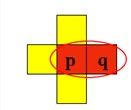
- 从具有坐标 ( x , y ) (x, y) (x,y)的像素 p p p到具有坐标 ( s , t ) (s, t) (s,t)的像素 q q q的一条通路由一系列具有坐标 ( x 0 , y 0 ) , ( x 1 , y 1 ) , … , ( x n , y n ) (x_0, y_0),(x_1, y_1),…,(x_n, y_n) (x0,y0),(x1,y1),…,(xn,yn)的独立像素组成。
- 这里 ( x 0 , y 0 ) = ( x , y ) , ( x n , y n ) = ( s , t ) (x_0, y_0) = (x, y),(x_n, y_n) = (s, t) (x0,y0)=(x,y),(xn,yn)=(s,t),且 ( x i , y i ) (x_i, y_i) (xi,yi)与 ( x i − 1 , y i − 1 ) (x_i-1, y_i-1) (xi−1,yi−1)连接,其 1 ≤ i ≤ n 1 ≤ i ≤ n 1≤i≤n,n为通路长度(即像素个数减1)
- 连接是连通的一种特例。
像素间距离
- 常用相似性、相关性度量指标
设3个像素 p 、 q 、 r p、q、r p、q、r,坐标为 ( x , y ) 、 ( s , t ) 、 ( u , v ) (x, y)、(s, t)、(u, v) (x,y)、(s,t)、(u,v),则其像素间的距离具有如下特性:
| 特性 | 公式 |
|---|---|
| 两个像素之间的距离总是正的(非负性) | D ( p , q ) ≥ 0 D(p, q) \geq 0 D(p,q)≥0,当且仅当 p = q p=q p=q |
| 距离与起止点的选择无关(对称性) | D ( p , q ) = D ( q , p ) D(p, q)=D(q, p) D(p,q)=D(q,p) |
| 最短距离是沿着直线的(两边之和大于等于第三边) | D ( p , r ) ≤ D ( p , q ) + D ( q , r ) D(p, r) \leq D(p, q) + D(q, r) D(p,r)≤D(p,q)+D(q,r) |
欧氏Euclidean距离 D E ( p , q ) D_E(p, q) DE(p,q)
D E ( p , q ) = [ ( x − s ) 2 + ( y − t ) 2 ] 1 / 2 D_E(p, q)=[(x - s)^2 + (y - t)^2]^{1/2} DE(p,q)=[(x−s)2+(y−t)2]1/2
城区city-block距离 D 4 ( p , q ) D_4(p, q) D4(p,q)
D 4 ( p , q ) = ∣ x − s ∣ + ∣ y − t ∣ D_4(p, q) = | x - s | + | y - t | D4(p,q)=∣x−s∣+∣y−t∣
棋盘chessboard距离 D 8 ( p , q ) D_8(p, q) D8(p,q)
D 8 ( p , q ) = m a x ( ∣ x − s ∣ , ∣ y − t ∣ ) D_8(p, q) = max(| x - s |, | y - t |) D8(p,q)=max(∣x−s∣,∣y−t∣)
附录
- 数字图像处理 第3版(姚敏 浙江大学等著)
- 数字图像处理入门-邻域、连通性、通路和距离