python异常值检测_利用Python进行异常值分析实例代码
前言
异常值是指样本中的个别值,也称为离群点,其数值明显偏离其余的观测值。常用检测方法3σ原则和箱型图。其中,3σ原则只适用服从正态分布的数据。在3σ原则下,异常值被定义为观察值和平均值的偏差超过3倍标准差的值。P(|x−μ|>3σ)≤0.003,在正太分布假设下,大于3σ的值出现的概率小于0.003,属于小概率事件,故可认定其为异常值。
异常值分析是检验数据是否有录入错误以及含有不合常理的数据。忽视异常值的存在是十分危险的,不加剔除地把异常值包括进数据的计算分析过程中,对结果会产生不良影响;重视异常值的出现,分析其产生的原因,常常成为发现问题进而改进决策的契机。
异常值是指样本中的个别值,其数值明显偏离其余的观测值。异常值也称为离群点,异常值的分析也称为离群点分析。
(1)简单统计量分析
可以先对变量做一个描述性统计,进而查看哪些数据是不合理的。最常用的统计量是最大值和最小值,用来判断这个变量的取值是否超出了合理的范围。如客户年龄的最大值为199岁,则该变量的取值存在异常。
(2)3原则
如果数据服从正态分布,在3原则下,异常值被定义为一组测定值中与平均值的偏差超过3倍标准差的值。在正态分布的假设下,距离平均值3之外的值出现的概率为P(|x-|>3)≤0.003,属于极个别的小概率事件。
如果数据不服从正态分布,也可以用远离平均值的多少倍标准差来描述。
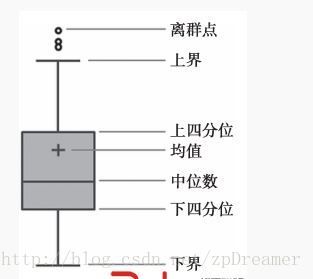
(3)箱型图分析
箱型图提供了识别异常值的一个标准:异常值通常被定义为小于QL-1.5IQR或大于QU+1.5IQR的值。QL称为下四分位数,表示全部观察值中有四分之一的数据取值比它小;QU称为上四分位数,表示全部观察值中有四分之一的数据取值比它大;IQR称为四分位数间距,是上四分位数QU与下四分位数QL之差,其间包含了全部观察值的一半。
箱型图依据实际数据绘制,没有对数据作任何限制性要求(如服从某种特定的分布形式),它只是真实直观地表现数据分布的本来面貌;另一方面,箱型图判断异常值的标准以四分位数和四分位距为基础,四分位数具有一定的鲁棒性:多达25%的数据可以变得任意远而不会很大地扰动四分位数,所以异常值不能对这个标准施加影响。由此可见,箱型图识别异常值的结果比较客观,在识别异常值方面有一定的优越性,如图3-1所示。
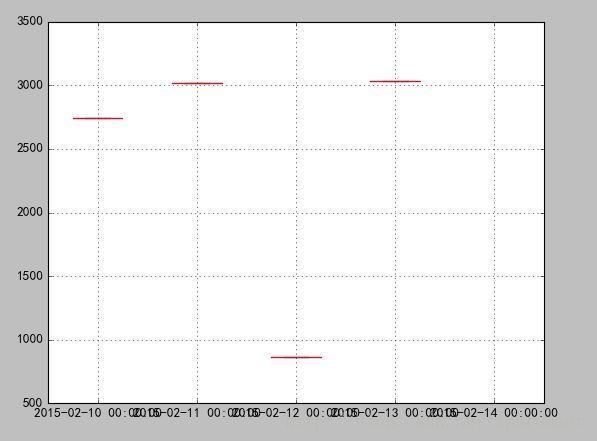
如下数据:
日期 2015/2/10 2015/2/11 2015/2/12 2015/2/13 2015/2/14
销量额 2742.8 3014.3 865 3036.8
我们对其进行异常值分析
import pandas as pd
catering_sale = 'data2.xls' #餐饮数据
data = pd.read_excel(catering_sale, index_col = u'日期') #读取数据,指定“日期”列为索引列
import matplotlib.pyplot as plt #导入图像库
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
plt.figure() #建立图像
p = data.boxplot() #画箱线图,直接使用DataFrame的方法
x = p['fliers'][0].get_xdata() # 'flies'即为异常值的标签
y = p['fliers'][0].get_ydata()
y.sort() #从小到大排序,该方法直接改变原对象
#用annotate添加注释
#其中有些相近的点,注解会出现重叠,难以看清,需要一些技巧来控制。
#以下参数都是经过调试的,需要具体问题具体调试。
for i in range(len(x)):
if i>0:
plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.05 -0.8/(y[i]-y[i-1]),y[i]))
else:
plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.08,y[i]))
plt.show()
结果如下:
总结
以上就是这篇文章的全部内容了,希望本文的内容对大家的学习或者工作具有一定的参考学习价值,如果有疑问大家可以留言交流,谢谢大家对脚本之家的支持。