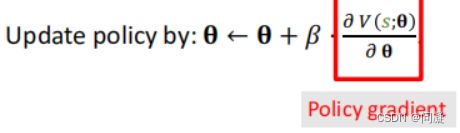策略学习(Policy-Based Reinforcement Learning)

---

前言

前面我们讲了强化学习的基本概念，这节课来说一说强化学习的策略学习（Policy-based）算法。

---

在进入正文之前说一句：策略学习的目标就是要用一个神经网络来近似策略函数，这个神经网络叫做策略网络（Policy Network），它可以用来控制agent运动；想要训练策略网络，就要用到Policy Gradient算法，该算法是策略学习的核心；还有中间计算策略梯度我仅仅是把推导公式列了出来，简要的说了一下，如果仅仅是应用强化学习算法解决问题，中间过程不太懂也没关系，就看看最后的策略梯度算法的过程理解一下就可以了；

一、策略学习

1.策略函数π（a|s）：它是一个概率密度函数，可以用来自动控制agent运动；它的输入是当前的状态s，输出是一个概率分布；

以超级玛丽这个游戏为例，假设给定当前状态s后，策略函数输出三个概率值，向左，向右和向上跳的概率分别为0.2,0.1和0.7；
代码如下（示例）：

这个例子里输入是状态s，输出是一个3行1列的列向量，向量的每一个元素是动作的概率，有了这三个概率值，agent做一次随机抽样，就得到了动作a，三个动作都有可能被抽到，但是向上的动作被抽到的概率最大，抽出动作a后，agent就做动作a；

2.求得策略网络的过程：以游戏为例，如果一个游戏只有五个状态，十个动作，那就有一个5*10的表格，那就很简单了，我们通过玩这个游戏把表里的每个概率算出来；

超级玛丽这样的游戏有无穷的状态，根本不可能把每个状态可能采取的动作都记录在一张表格里，超级玛丽这个游戏我们就没有办法直接计算策略函数，大部分情况下都没有办法直接计算策略函数，所以要做函数近似；函数近似的方法有很多种：线性函数，kernel函数，神经网络，我们当然是要用神经网络去近似策略函数喽^-;

我们使用π（a|s;θ）近似π（a|s）；θ是神经网络的参数，一开始并不知道，是随机初始化的，通过学习来改进θ；

介绍完策略学习的一些概念后，开始介绍策略学习喽

3.策略学习

我们的目标就是近似Vπ(st)，Vπ(st)是对状态价值函数求的期望值，那么根据agent采取的动作是离散值还是连续值，下面是action为离散和连续的时候Vπ(st)的计算公式

我们使用神经网络来近似Vπ(st)，把Vπ(st)的π（即策略函数）用神经网络来近似，Vπ(st)就变成了下面的形式：
Qusetion：怎么样让策略网络变得越来越好呢？答案就是改进模型参数θ，让V（st;θ）变得越来越大，因此我们就把目标函数定义为了V（st;θ）的期望，这个期望是关于状态s求的，把状态s作为随机变量，求其期望值s就被去掉了，就是一个关于θ的函数了，那就让J（θ）越大越好；
要让J（θ）越来越大，就需要使用策略梯度（Policy Gradient）的方法；

让agent玩游戏，每一步观测到不同的状态s，（状态s相当于从状态的概率分布随机抽样得到的）；把V（s;θ）关于θ求导，得到它的梯度后，用梯度上升的方法来更新θ，这很类似于随机梯度上升，随机性来源于状态s，我们计算的应该J（θ）关于θ的导数，这才是更新θ用到的梯度，这里我们计算的是V（s;θ）关于θ的导数，因为我们不可能在开始玩游戏的时候就知道所有的状态s；V（s;θ）关于θ的导数被称为策略梯度；

4.计算策略梯度（Policy Gradient）：

在计算梯度时我们假设Qπ（s,a）不依赖于策略π，（事实上是依赖于π的），仅仅是为了方便理解，不是特别严谨，如果你只是用策略梯度的算法，这么理解就可以了；最终得到计算策略梯度的公式：

注意上面计算V（s;θ）关于θ的导数是action是连续值的时候，action为离散值的情况很简单，直接在最后列出离散值情况的公式了；

最终我们得到了action为离散值和连续值两种情况的公式：

5.策略梯度算法的过程：

在t时刻观测到状态st；

然后用蒙特卡洛近似来计算策略梯度，把策略网络π作为概率密度函数，用策略网络π随机抽样得到一个动作at；

计算动作价值函数的值，把结果即为qt；

对策略网络π求导，算出对于θ的梯度；

近似的计算策略梯度；

更新策略网络；

一个问题：我们并不知道怎么计算qt即动作价值函数的值；

两种方法：1.REINFORCE：一种叫做REINFORCE的算法，用策略网络π来控制agent运动，一直玩到游戏结束，把整个游戏的轨迹记录下来s1,a1,r1,s2,a2,r2,…,st,at,rt;观测到所欲的奖励rt，就计算出来ut，（注意这里的ut是Ut的观测值）因为Qπ（st,at）= E（Ut），我们用观测值ut代替Qπ（st,at），即qt=ut这是一种近似；

2.用神经网络近似Qπ，这样就用了两个神经网络，近似Qπ（s,a）的神经网络q（s,a;w）（称为价值网络）被称为critic，另一个近似π（a|s）的神经网络（称为策略网络）π（a|s,θ）称为actor；这样就引出了actor-critic method；接下来会介绍acrot-critic method；

总结

以上就是今天要讲的内容，本文仅仅简单介绍了策略学习方法，如有错误请谅解并指正。