异常点检测算法（隔离森林、局部离群因子）

前言

• 本次数据采用孕妇吸烟与胎儿健康数据集
• 基于sklearn包中异常点检测方法
• 本文分别使用IsolationForest（隔离森林）、LocalOutlierFactor（局部离群因子）两种异常值检测算法对同一数据集进行异常值检测，并观察结果
• 参考资料：IsolationForest官方文档、LocalOutlierFactor官方文档、刘建平老师关于异常值检测算法的小结

导入包

import pandas as pd
import numpy as np

import matplotlib as mpl
import matplotlib.pyplot as plt
#中文显示问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False

from sklearn.ensemble import IsolationForest
from sklearn.neighbors import LocalOutlierFactor

数据预处理

from sklearn.ensemble import IsolationForest
name = ['序号','新生儿体重','孕妇怀孕期','新生儿胎次状况','孕妇怀孕时年龄','孕妇怀孕前身高','孕妇怀孕前体重','孕妇吸烟状况']
df = pd.read_csv("D:/学习资料/数学/数学建模培训与比赛/孕妇吸烟与胎儿健康/data0901.txt", sep = '\t',names = name,encoding="gbk",index_col = '序号')

df = df[['新生儿体重','孕妇怀孕期']]
# 剔除缺失值
df = df[df['孕妇怀孕期'] < 999]
df.head()

plt.figure(dpi = 600,figsize = (9,5))
plt.plot(df['孕妇怀孕期'],df['新生儿体重'],'+')
plt.xlabel('孕妇怀孕期')
plt.ylabel('新生儿体重')
# plt.savefig('散点图')

IsolationForest

• n_estimators：弱学习器个数，个数越多模型越稳定，但太多容易过拟合
• max_samples：从数据中抽取的样本数，用于训练每个基估计量，当该参数大于样本数时，所有样本都将用来构建树。一般使用'auto'就好，因为当该参数大于256后模型效果提升不明显
• contamination：异常样本占比，该参数将影响异常与正常得分界限的阈值，需要根据数据集情况确定，无固定值，但数值应在$(0,0.5]$内
• random_state：随机数种子，方便复现结果
• 更多参数请查阅官方文档

fre_model = IsolationForest(n_estimators = 100,
                            max_samples = 'auto',
                            contamination = 0.015,
                            random_state = 42)
# 训练模型
fre_model.fit(df[['孕妇怀孕期','新生儿体重']].values)

# decision_function得到异常评分
df['fre_scores']  = fre_model.decision_function(df[['孕妇怀孕期','新生儿体重']].values)
# predict用于判断是否异常(-1为异常，1为正常)
df['fre_anomaly'] = fre_model.predict(df[['孕妇怀孕期','新生儿体重']].values)
df.head()

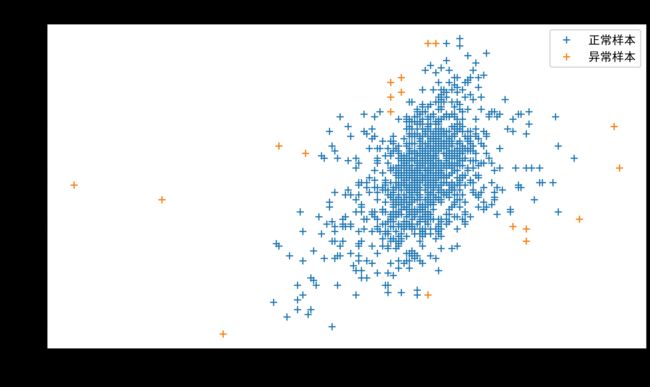
plt.figure(dpi = 600,figsize = (9,5))
plt.title("IsolationForest")
plt.plot(df['孕妇怀孕期'],df['新生儿体重'],'+')
plt.plot(df['孕妇怀孕期'][df['fre_anomaly'] == -1],df['新生儿体重'][df['fre_anomaly'] == -1],'+')
plt.legend(['正常样本','异常样本'])
plt.xlabel('孕妇怀孕期')
plt.ylabel('新生儿体重')
# plt.savefig('隔离森林.png')

LocalOutlierFactor

• n_neighbors：考虑的k个近邻数，在实践中，当n_neighbors = 20通常能算法有较好的表现。当离群点的比例较高时，n_neighbors应该较大（如n_neighbors = 35）。
• contamination：异常样本占比，该参数将影响异常与正常得分界限的阈值，需要根据数据集情况确定，无固定值，但数值应在$(0,0.5]$内
• novelty：当仅作为异常样本检测时novelty设为Flase，当使用算法进行新奇点(用于新的、未见过数据)检测时novelty设为True
• 更多参数请查阅官方文档

lof_model = LocalOutlierFactor(n_neighbors=20,
                               contamination = 0.015,
                               novelty=False)
df['lof_anomaly'] = lof_model.fit_predict(df[['孕妇怀孕期','新生儿体重']].values)
df['lof_score'] = lof_model.negative_outlier_factor_
df.head()

plt.figure(dpi = 600,figsize = (9,5))
plt.title("Local Outlier Factor (LOF)")
plt.plot(df['孕妇怀孕期'],df['新生儿体重'],'+')
plt.plot(df['孕妇怀孕期'][df['lof_anomaly'] == -1],df['新生儿体重'][df['lof_anomaly'] == -1],'+')
plt.legend(['正常样本','异常样本'])
plt.xlabel('孕妇怀孕期')
plt.ylabel('新生儿体重')
plt.savefig('局部离群因子.png')

算法优缺点总结

IsolationForest

优点

• 是目前异常点检测最常用的算法之一，几乎成为异常点检测算法的首选项
• 利用集成学习的思路来做异常点检测
• 具有线性时间复杂度
• 树的数量越多，算法越稳定
• 每棵树都是互相独立生成的，因此可以部署在大规模分布式系统上来加速运算

缺点

• 不适用于特别高维的数据，由于每次切数据空间都是随机选取一个维度和该维度的随机一个特征，建完树后仍然有大量的维度没有被使用，导致算法可靠性降低
• 仅对即全局稀疏点敏感，不擅长处理局部的相对稀疏点 ，这样在某些局部的异常点较多的时候检测可能不是很准

LocalOutlierFactor

优点

• 能对对轻度高维数据集(即维数勉强算是高维)实现异常值检测
• 考虑到数据集的局部和全局属性：即使在具有不同潜在密度的离群点数据集中，它也能够表现得很好。
• 问题不在于样本是如何被分离的，而是样本与周围近邻的分离程度有多大。
• 算法可被用于新的未见过数据上

缺点

• 仍然不擅长处理高维度数据集