Using Python to Solve GA Classic Problems-Facility-Location Set-Covering Problem

Solutions

data processing

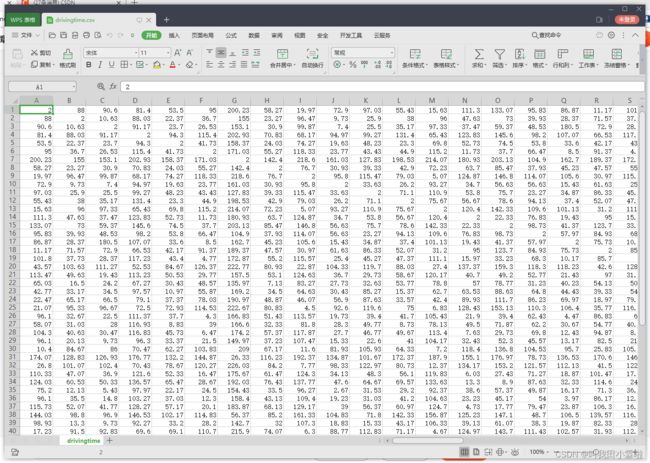From the dataset, we can see that all the data are symmetric matrices about the main diagonal. The size is 58 * 58.

problem analysis

• For example：The time A ——> B is 15min，also The time B ——> A is 15min. That means that only one 15min facility in A or B town can meet the demand, rather than both A and B need to be built.
• Only one facility needs to be built in each town, so that the facility can meet the requirements of going to other towns. The total number of facilities is therefore 58. (If there is no isolated town）
• Through iteration, we can find a solution that costs as little as possible. For example, 15 min facilities can be used instead of 20 min facilities.

data processing

• Through problem analysis 1. In fact, half of the data in the chart can be deleted. The upper triangular matrix and the lower triangular matrix express the same meaning. Here I set the duplicate data to 0.
• Since the element of the main diagonal is equal to 2, it is also set as 0 here. As for why, I will talk about it later.

My thoughts

Answering ideas

1. Initialize 20 samples as the population class. Population matrix size: 20 * 58 * 58
2. Disrupt the population matrix. So that the matrix of all samples therein is not an upper triangular matrix or a lower triangular matrix. Population matrix size: 20 * 58 * 58
3. The parent class crossover between two pairs, and the crossover proportion is also random. The crossover method is matrix cutting and splicing. Two samples of parents were randomly cut in the same proportion, and then spliced. Generate two offspring and check the rationality of the two offspring. Rationality check will be discussed separately below. Place the generated descendant with the population class. Population matrix size: 40*58*58
4. Through the loss function, all samples in the population are sorted, and the first 20 samples are retained as the new generation population. Output the loss value of the best and worst samples at the same time. Population matrix size: 20*58*58
5. If the optimal loss value and the worst loss value are equal, the mutation is performed. Variation is also discussed separately below. Population matrix size：20*58*58
6. Repeat 3, 4 and 5 for iteration。

Rationality check

Rationality check refers to that data cannot appear at the same time in the main diagonal game position in the sample matrix (size: 58 * 58)

For example：sample A[ i, j ]和 A[ j, i ] are about the principal diagonal symmetry. Because the expression means the time from town i to town j, we can draw this conclusion according to the first article of the above problem analysis. So if both A [i, j] and A [j, i] have data. Then you need to delete one randomly.

Mutation

My variation ratio is 20%, and all samples in the population will be mutated.

The non-zero symmetric data on the main diagonal in the sample matrix (size: 58 * 58) are exchanged.

For example：sampleA[ i, j ]和 A[ j, i ] are about the principal diagonal symmetry. At this time, it is feasible to exchange the values of A [i, j] and A [j, i] because the meaning of the expression remains unchanged.

Execution effect

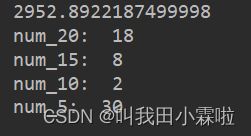
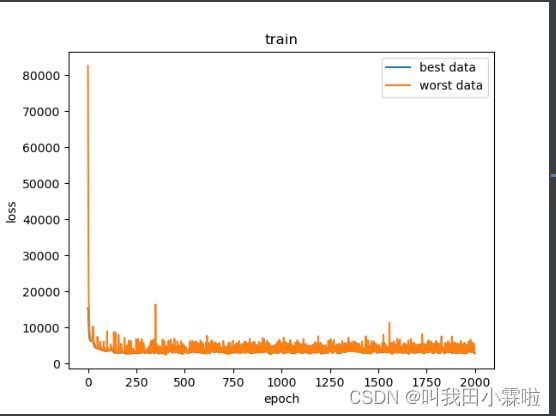
500epoch

 2000epoch

Result analysis

In fact, the results of each run are different, but they tend to the same output. Here, it has been run twice randomly, and there may be some deviation.

Although from the results, the data loss value of 2000 iterations is higher than that of 500 iterations. However, 500 times of facility layout may be more appropriate. Here I think of the problem of loss function.

Definition of my loss function (for a single sample):

       

From the loss function, we can see that the method used is variance. In fact, my original intention is to make the data in each row of the matrix approximately equal.

However, this will lead to another problem. If there is only one data in a row, the variance will be 0, but it may not meet the optimal solution. Therefore, after more iterations, this trend becomes more obvious, leading to over fitting.

Why is the main diagonal element set to 0?

It is mentioned above that the data of the main diagonal of the dataset is set to 0, because the elements of the main diagonal will affect the loss function, and it is meaningless. In the Excel output of the final result, it can be observed that the maximum value of many lines is 0, and the maximum value is 2, which is itself. Then the facilities set for 5min can meet the requirements.