动手学深度学习（十八）——LeNet：CNN经典网络（一）

讲解LeNet的材料比较多，这个Blog的内容主要是李沐老师《动手学深度学习V2》课程的markdown文件。

LeNet还是比较简单的，根据目录跳转到自己想看的部分吧！

---

1. 卷积神经网络（LeNet）发展

    LeNet，它是最早发布的卷积神经网络之一，因其在计算机视觉任务中的高效性能而受到广泛关注。这个模型是由 AT&T 贝尔实验室的研究员 Yann LeCun 在1989年提出的（并以其命名），目的是识别图像 LeCun.Bottou.Bengio.ea.1998 中的手写数字。
    当时，Yann LeCun 发表了第一篇通过反向传播成功训练卷积神经网络的研究，这项工作代表了十多年来神经网络研究开发的成果。当时， LeNet 取得了与支持向量机（support vector machines）性能相媲美的成果，成为监督学习的主流方法。LeNet 被广泛用于自动取款机（ATM）机中，帮助识别处理支票的数字。
    时至今日，一些自动取款机仍在运行 Yann LeCun 和他的同事 Leon Bottou 在上世纪90年代写的代码呢！

---

2. LeNet网络结构

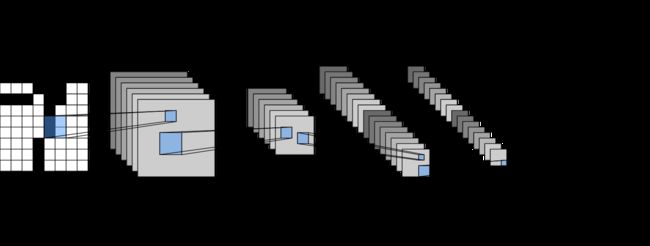
总体来看，(LeNet（LeNet-5）由两个部分组成：

• 卷积编码器：由两个卷积层组成;
• 全连接层密集块：由三个全连接层组成。

该结构如下所展示。

    每个卷积块中的基本单元是一个卷积层、一个 sigmoid 激活函数和平均池化层。请注意，虽然 ReLU 和最大池化层更有效，但它们在20世纪90年代还没有出现。每个卷积层使用 $5\times 5$ 卷积核和一个 sigmoid 激活函数。这些层将输入映射到多个二维特征输出，通常同时增加通道的数量。第一卷积层有 6 个输出通道，而第二个卷积层有 16 个输出通道。每个 $2\times 2$ 池操作（步骤2）通过空间下采样将维数减少 4 倍。卷积的输出形状由批量大小、通道数、高度、宽度决定。

    为了将卷积块的输出传递给稠密块，我们必须在小批量中展平每个样本。换言之，我们将这个四维输入转换成全连接层所期望的二维输入。这里的二维表示的第一个维度索引小批量中的样本，第二个维度给出每个样本的平面向量表示。LeNet 的稠密块有三个全连接层，分别有 120、84 和 10 个输出。因为我们仍在执行分类，所以输出层的 10 维对应于最后输出结果的数量。

    通过下面的 LeNet 代码，你会相信用深度学习框架实现此类模型非常简单。我们只需要实例化一个 Sequential 块并将需要的层连接在一起。

总结：

1. LeNet早期成功的神经网络
2. 先使用卷积层来学习图片空间信息
3. 然后使用全连接层来转换到类别空间

3. 代码实现（将LeNet应用在简单的Fashion-MNIST上）

3.1 导入相关包

import torch
from torch import nn
from d2l import torch as d2l

3.2 网络结构定义及验证

class Reshape(torch.nn.Module):
    """将数据转换成批量数不变、通道数为1，大小为（28，28）的数据"""
    def forward(self, x):
        return x.view(-1, 1, 28, 28)

net = torch.nn.Sequential(
    Reshape(), 
    nn.Conv2d(1, 6, kernel_size=5,padding=2), 
    nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(), nn.Linear(84, 10))

检查网络结构
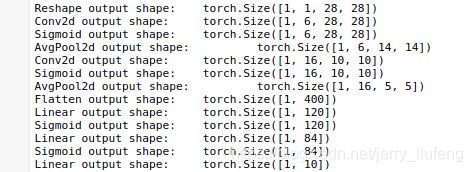
    我们对原始模型做了一点小改动，去掉了最后一层的高斯激活。除此之外，这个网络与最初的 LeNet-5 一致。下面，我们将一个大小为 $28\times 28$ 的单通道（黑白）图像通过 LeNet。 通过在每一层打印输出的形状，我们可以[检查模型]，以确保其操作与我们期望的

# 检查模型
X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__, 'output shape: \t', X.shape)

其中值的注意的是：
    在整个卷积块中，与上一层相比，每一层特征的高度和宽度都减小了。第一个卷积层使用 2 个像素的填充，来补偿 $5\times 5$ 卷积核导致的特征减少。相反，第二个卷积层没有填充，因此高度和宽度都减少了 4 个像素。随着层叠的上升，通道的数量从输入时的 1 个，增加到第一个卷积层之后的 6 个，再到第二个卷积层之后的 16 个。同时，每个池化层的高度和宽度都减半。最后，每个全连接层减少维数，最终输出一个维数与结果分类数相匹配的输出。

---

3.3 模型训练

现在我们已经实现了 LeNet ，让我们看看LeNet在Fashion-MNIST数据集上的表现。

from torchvision import transforms
import torchvision
from torch.utils import data

batch_size = 256

def get_dataloader_workers():
    """使用四个进程读取数据"""
    return 4

def load_data_fashion_mnist(batch_size,resize=None):
    """下载Fashion-MNIST数据集，并将其保存至内存中"""
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0,transforms.Resize(resize)) # transforms.Resize将图片最小的一条边缩放到指定大小，另一边缩放对应比例
    trans = transforms.Compose(trans) # compose用于串联多个操作
    mnist_train = torchvision.datasets.FashionMNIST(root="./data",
                                                    train=True,
                                                    transform=trans,
                                                    download=True)
    mnist_test = torchvision.datasets.FashionMNIST(root="./data",
                                                   train=False,
                                                   transform=trans,
                                                   download=True)
    return (data.DataLoader(mnist_train,batch_size,shuffle=True,
                           num_workers=get_dataloader_workers()),
           data.DataLoader(mnist_test,batch_size,shuffle=True,
                          num_workers = get_dataloader_workers()))

batch_size = 256
train_iter, test_iter = load_data_fashion_mnist(batch_size=batch_size)

虽然卷积神经网络的参数较少，但与深度的多层感知机相比，它们的计算成本仍然很高，因为每个参数都参与更多的乘法。如果你有机会使用GPU，可以用它加快训练。

为了进行评估，我们需对 softmax回归算法处理Fashion-MNIST算法中描述的evaluate_accuracy函数进行轻微的修改。由于完整的数据集位于内存中，因此在模型使用 GPU 计算数据集之前，我们需要将其复制到显存中。

def evaluate_accuracy_gpu(net, data_iter, device=None):  #@save
    """使用GPU计算模型在数据集上的精度。"""
    if isinstance(net, torch.nn.Module):
        net.eval()  # 设置为评估模式
        if not device:
            device = next(iter(net.parameters())).device
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)
    for X, y in data_iter:
        if isinstance(X, list):
            # BERT微调所需的（之后将介绍）
            X = [x.to(device) for x in X]
        else:
            X = X.to(device)
        y = y.to(device)
        metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

[为了使用 GPU，我们还需要一点小改动]。
与 softmax 中定义的 train 不同，在进行正向和反向传播之前，我们需要将每一小批量数据移动到我们指定的设备（例如 GPU）上。

    如下所示，训练函数 train 也类似于softmax 中定义的 train 。由于我们将实现多层神经网络，因此我们将主要使用高级 API。以下训练函数假定从高级 API 创建的模型作为输入，并进行相应的优化。我们使用在 初始化参数xavier 中介绍的 Xavier 随机初始化模型参数。与全连接层一样，我们使用交叉熵损失函数和小批量随机梯度下降。

#@save
def train(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型"""
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)

    net.apply(init_weights)
    print('training on', device)
    net.to(device) # 将网络挪到gpu上
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，范例数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
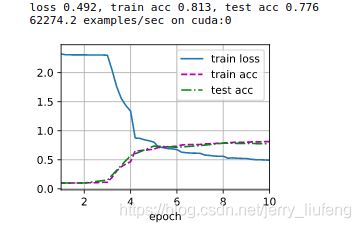
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')

3.4 训练结果

lr, num_epochs = 0.9, 10
train(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

1. 对比之前使用softmax进行回归分类得到的结果，LeNet的loss进一步降低，精度提高了一些。仔细调整LeNet的参数（如learning rate、卷积kernel大小、padding大小、输出通道数等等）其对我们使用的Fashion-MNIST数据集的分类精确取大概能达到84%,当然这就是炼丹了。

2. 训练10个epoch我这里没有明显的过拟合，但是增加迭代次数还是会有过拟合的风险的，所以使用一些我们之前章节中提及的解决过拟合的方法就有了勇武之地了，在后面的章节中也将继续实际应用起来，包括dropout、正则化、初始化参数等等。