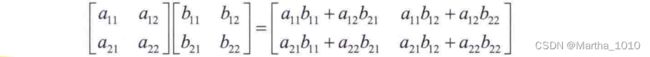数字图像处理--冈萨雷斯第4版--第二章 数字图像基础
数字图像处理--冈萨雷斯版--第二章
- 第二章 数字图像基础
-
- 2.1 视觉感知要素
-
- 2.1.1 人眼的结构
- 2.1.2 人眼中图像的形成
- 2.1.3 亮度适应与辨别
- 2.2 光和电磁波谱
- 2.3 图像感知与获取
-
- 2.3.1 使用单个传感器获取图像
- 2.3.2 使用条带传感器获取图像
- 2.3.3 使用阵列传感器获取图像
- 2.3.4 一个简单的成像模型
- 2.4 图像取样和量化
-
- 2.4.1 取样和量化的基本概念
- 2.4.2 数字图像表示
- 2.4.3 线性索引和坐标索引
- 2.4.4 空间分辨率和灰度分辨率
- 2.4.5 图像内插
- 2.5 像素间的一些基本关系
-
- 2.5.1 像素的相邻像素
- 2.5.2 邻接、连通、区域、边界
- 2.5.3距离测度
- 2.6 数字图像处理所用的基本数学工具介绍
-
- 2.6.1 对应元素运算和矩阵运算
- 2.6.2 线性运算与非线性运算
- 2.6.3 算术运算
- 2.6.4 集合运算和逻辑运算
- 2.6.5 空间运算
- 2.6.6 向量与矩阵运算
- 2.6.7 图像变换
- 2.6.8 图像灰度和随机变量
第二章 数字图像基础
2.1 视觉感知要素
图像形成并被人类感知的基本原理，并根据数字图像处理时所用的一些要素来了解人类视觉的物理限制
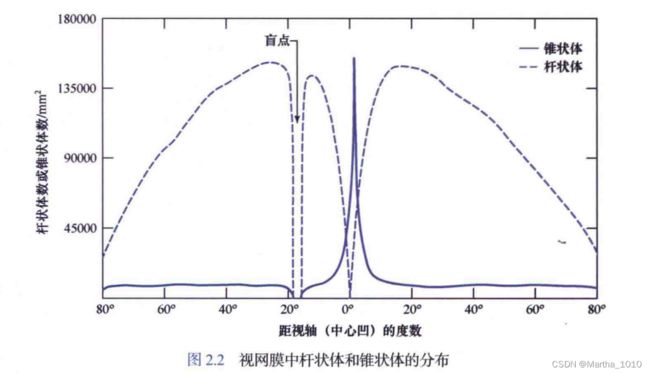
2.1.1 人眼的结构
人眼的解剖结构
杆状体和锥状体：两类光感受器
| 光感受器 | 数量 | 分布位置 | 特性 |
|---|---|---|---|
| 锥状体 | 600~700万个 | 主要分布在视网膜中央凹 | 对颜色高度敏感；每个锥状体连接自身的神经末梢，肌肉控制眼球转动，使部分区域图像落在中央凹，分辨细节；锥状体视觉被称为明/亮视觉 |
| 杆状体 | 7500~1500万个 | 分布面积大 | 捕获视野中的整个图像；没有色觉，对低光照敏感；杆状体视觉被称为暗/微光视觉 |
2.1.2 人眼中图像的形成
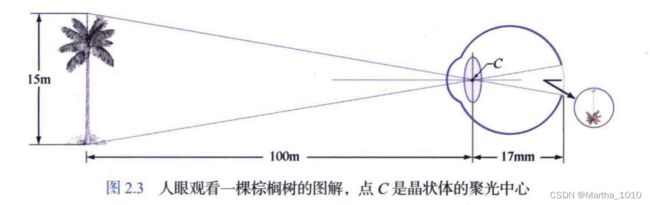
普通照相机：镜头的焦距固定，通过改变镜头和成像平面之间的距离来实现不同距离的焦距
人眼：晶状体与成像区域(视网膜)之间的距离是固定的，通过改变晶状体的形状得到正确聚焦的焦距
视网膜图像主要聚焦在中央凹区域，光感受器的相对激励作用产生感知，把辐射能量转换为最终由大脑解码的电脉冲
2.1.3 亮度适应与辨别
主观亮度：人类视觉系统感知的亮度
低照明级别，视觉由杆状体执行
高照明级别，视觉由锥状体执行
感知亮度不是实际灰度的简单函数
1.视觉系统往往会在不同灰度区域的边界处出现"下冲"或"上冲"现象，如马赫带现象
2.一个区域的感知亮度并不只是取决于其灰度，如同时对比现象
2.2 光和电磁波谱
波长(λ)和频率(v)的关系
λ = c v \lambda = \frac{c}{v} λ=vc
c = 2.998*10^8 m/s 是光速
电磁波谱各分量的能量为
E = h v E=hv E=hv
电磁波可视为以波长λ传播的正弦波，或视为没有质量的粒子流，每个粒子像波浪一样行进并以光速运动，每个无质量的粒子都是具有一定能量的粒子，频率越高，能量越高。
可见光谱
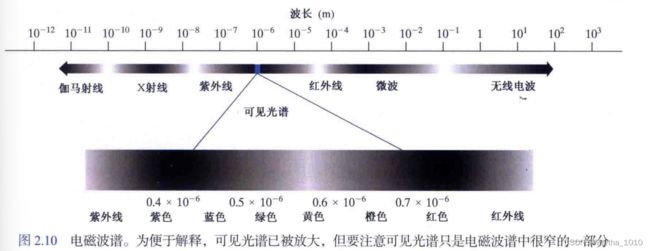
感知物体的颜色由物体反射的光的性质决定，例如，绿色物体主要反射波长范围为500~570nm的光，并吸收其他波长的大部分能量
单色光：没有颜色的光，唯一属性是亮度，单色光从黑到白的数值范围通常称为灰度级，单色图像通常称为灰度图像
2.3 图像感知与获取
大多图像的产生：“照射”源和形成图像的“场景”元素对光能的反射或吸收
在某些应用中，反射的能量或透射的能量被聚焦到一个光转换器上，光转换器把能量转换成可见光
组合输入电能和传感器对正被检测能量的响应，将入射能量转换成电压。输出电压波形是传感器的响应，将传感器响应数字化，得到一个数字量
2.3.1 使用单个传感器获取图像
要使用单个传感器生成二维图像，传感器和成像区域之间必须要有x方向和y方向的相对位移。
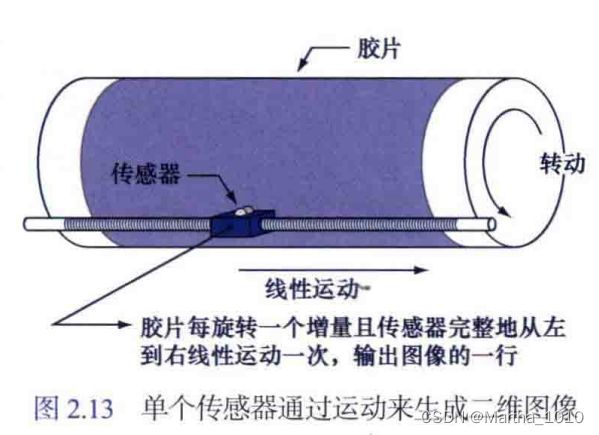
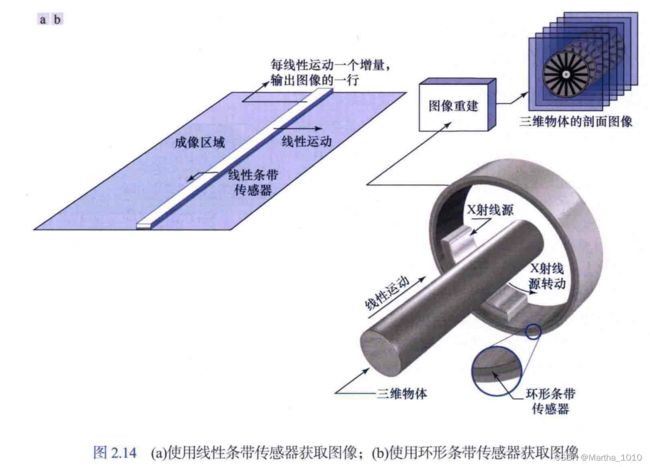
2.3.2 使用条带传感器获取图像
2.3.3 使用阵列传感器获取图像
以二维阵列形式排列各个感测元件
CCD(电荷耦合器件)阵列：可制造成具有较宽范围的传感特性，并能封装成具有更多单元的稳定阵列
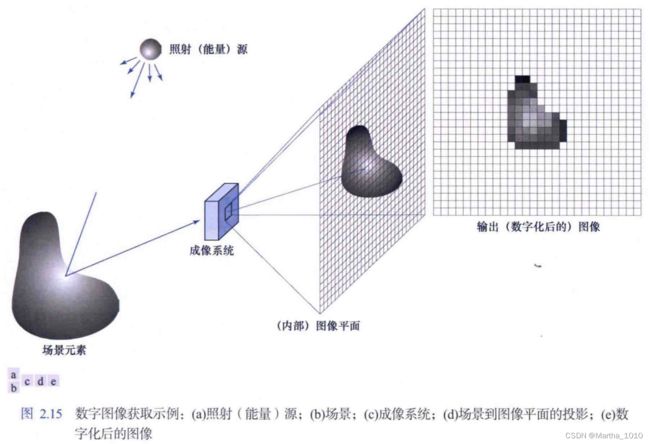
2.3.4 一个简单的成像模型
f(x,y)来表示图像，在某一空间坐标处的f的值是一个标量，与物理源辐射的能量成正比，f(x,y)一定是非负的和有限的
0 ≤ f ( x , y ) < ∞ 0\le f(x,y)<\infty 0≤f(x,y)<∞
同时
f ( x , y ) = i ( x , y ) r ( x , y ) f(x,y)=i(x,y)r(x,y) f(x,y)=i(x,y)r(x,y)
0 ≤ i ( x , y ) < ∞ 0\le i(x,y)<\infty 0≤i(x,y)<∞
0 ≤ r ( x , y ) < 1 0\le r(x,y)<1 0≤r(x,y)<1
i(x,y)入射分量，取决于照射源
r(x,y)反射分量，取决于被成像物体的特性，限制在0(全吸收)1(全反射)之间
在投射成像的情况下，r(x,y)是透射分量
2.4 图像取样和量化
2.4.1 取样和量化的基本概念
将一幅连续图像f转换为数字形式
取样(采样)：对函数坐标值数字化
量化：对函数幅度值进行数字化
以条带传感器为例
2.4.2 数字图像表示
1.三维图像表示
2.可视灰度矩阵表示
3.二维数值阵列表示：矩阵中的每一个单元称为图像单元、图像元素或像素
MxN的数字图像的中心，M/N除以2后四舍五入最接近的整数得到
离散灰度级数L通常取2的整数次幂
L = 2 k L=2^k L=2k
动态范围：灰度跨越的值域
存储数字图像所需的比特数b:
b = M N k b=MNk b=MNk
当一幅图像具有2^k个可能的灰度级时，我们称该图像是一幅k比特图像
如256级图像称为一幅8比特图像
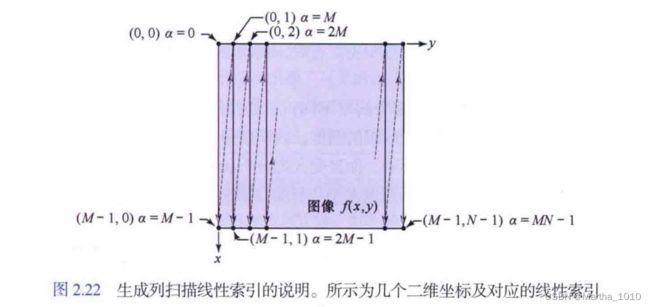
2.4.3 线性索引和坐标索引
线性索引：由一个一维的非负整数串组成
分为行扫描和列扫描
坐标索引：由二维坐标索引
2.4.4 空间分辨率和灰度分辨率
空间分辨率：图像中最小可辨别细节的测度
如何定量的说明空间分辨率:使用单位距离的线对数和单位距离的点数(像素数)
点数/英寸(dpi)：单位距离内可分辨的最大线对数，是印刷和出版业中常用的图像分辨率的测度
空间分辨率的测度必须针对空间单位声明才有意义，如果未声明图像包含的空间维数，那么说一幅图像的分辨率是没有意义的
灰度分辨率：灰度级中可分辨的最小变化，灰度级数通常是2的整数次幂，最常用的数是8比特；灰度分辨率通常是指量化灰度时所用的比特数（如8bit）
空间和灰度分辨率之间可能存在的关系
三类图像的等偏爱曲线
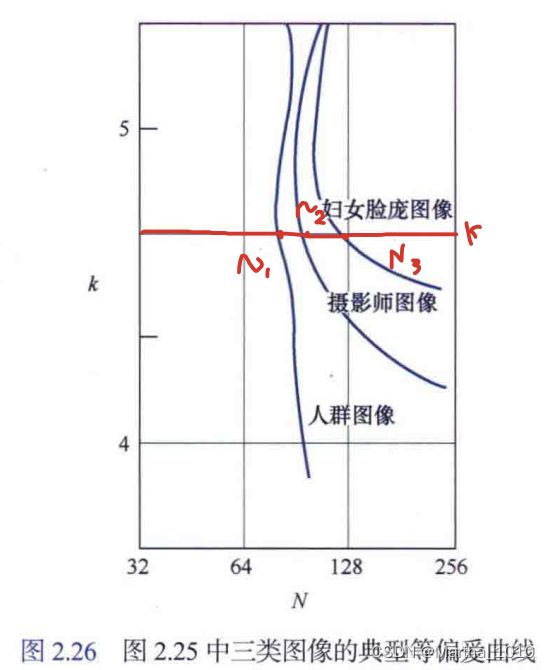
等偏爱曲线上的点对应于等主观质量的图像，越接近右上角喜爱程度越高
2.4.5 图像内插
内插：用已知数据来估计未知位置的值的过程
例：如何将大小为500x500像素的一幅图像放大到750x750像素？
最近邻内插：创建一个750x750的假想网格，网格的像素间隔完全于原图像的像素间隔相同，然后收缩网格，使其完全于原图像重叠，收缩后的像素间隔要小于原图像，我们再下伏原图像中找到最接近的像素，并把该像素的灰度赋给750x750网格中的新像素
缺点：会产生人为失真
双线性内插：使用4个最近邻灰度计算给定位置的灰度
v ( x , y ) = a x + b y + c x y + d v(x,y)=ax+by+cxy+d v(x,y)=ax+by+cxy+d
4个系数可由4个最近邻点写出的4个未知方程求出
双三次内插：包括16个最近邻点
v ( x , y ) = ∑ i = 0 3 ∑ j = 0 3 a i j x i y j v(x,y)=\sum_{i=0}^{3} \sum_{j=0}^{3}a_{ij}x^iy^j v(x,y)=i=0∑3j=0∑3aijxiyj
2.5 像素间的一些基本关系
2.5.1 像素的相邻像素
4邻域(N_4( p ))：(x+1,y), (x-1,y), (x,y+1), (x,y-1)
4对角相邻像素(N_D( p ))：(x+1,y+1), (x+1,y-1), (x-1,y+1), (x-1,y-1)
8邻域：两者之和
2.5.2 邻接、连通、区域、边界
V是用于定义邻接的灰度值集合
三种类型的邻接
混合邻接示意图
2.5.3距离测度
欧几里得距离
D e ( p , q ) = [ ( x − u ) 2 + ( y − v ) 2 ] 1 2 D_e(p,q)=[(x-u)^2+(y-v)^2]^\frac{1}{2} De(p,q)=[(x−u)2+(y−v)2]21
城市街区距离
D 4 ( p , q ) = ∣ x − u ∣ + ∣ y − v ∣ D_4(p,q)=|x-u|+|y-v| D4(p,q)=∣x−u∣+∣y−v∣
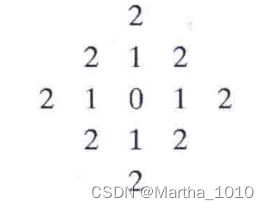
棋盘距离
D 8 ( p , q ) = m a x ( ∣ x − u ∣ , ∣ y − v ∣ ) D_8(p,q)=max(|x-u|,|y-v|) D8(p,q)=max(∣x−u∣,∣y−v∣)
2.6 数字图像处理所用的基本数学工具介绍
2.6.1 对应元素运算和矩阵运算
对应元素运算
矩阵运算
2.6.2 线性运算与非线性运算
线性运算
H [ f ( x , y ) ] = g ( x , y ) H[f(x,y)]=g(x,y) H[f(x,y)]=g(x,y)
H [ a f 1 ( x , y ) + b f 2 ( x , y ) ] = a H [ f 1 ( x , y ) ] + b H [ f 2 ( x , y ) ] = a g 1 ( x , y ) + b g 2 ( x , y ) H[af_1(x,y)+bf_2(x,y)]=aH[f_1(x,y)]+bH[f_2(x,y)]=ag_1(x,y)+bg_2(x,y) H[af1(x,y)+bf2(x,y)]=aH[f1(x,y)]+bH[f2(x,y)]=ag1(x,y)+bg2(x,y)
如求和算子Σ
非线性运算
非线性算子如最大值算子
2.6.3 算术运算
使用图像相加平均/降低噪声：对K幅不同的噪声图像取平均值
使用图像相减比较图像
使用图像相乘/相除校正阴影和模板
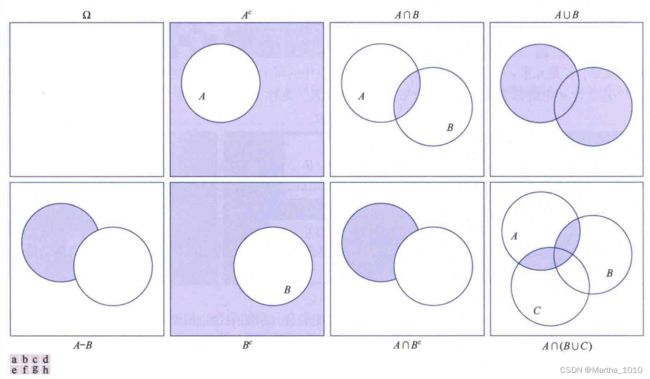
2.6.4 集合运算和逻辑运算
2.6.5 空间运算
单像素运算
s = T ( z ) s=T(z) s=T(z)
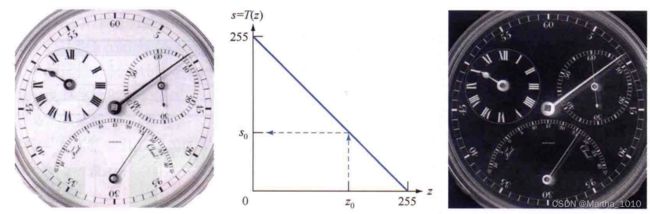
邻域运算
g ( x , y ) = 1 m n ∑ ( r , c ) ∈ S x y f ( r , c ) g(x,y)=\frac{1}{mn}\sum_{(r,c)\in S_{xy}}f(r,c) g(x,y)=mn1(r,c)∈Sxy∑f(r,c)
可进行局部平均
几何空间变换
改变图像中像素的空间排列，通常称为橡皮膜变换，类似于再一块橡皮膜上打印图像，然后根据预定义的一组规则来拉伸或收缩橡皮膜
由两种基本运算组成
（1）坐标的空间变换
（2）灰度内插
仿射变换
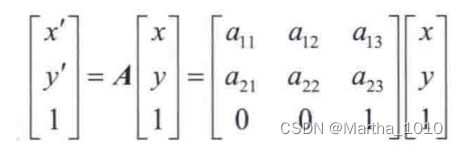
可以用该矩阵来表示所有4个仿射变换：缩放变换，平移变换，旋转变换，剪切变换
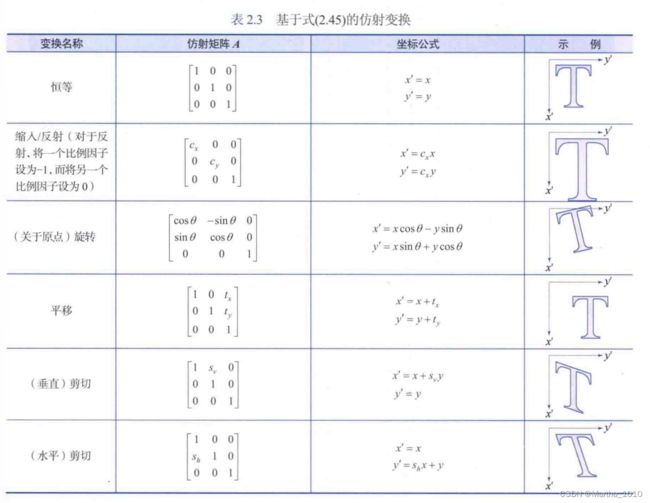
图像旋转和灰度内插
图像配准
2.6.6 向量与矩阵运算
多光谱图像处理
