判别模型和生成模型的区别
20210703
https://www.zhihu.com/question/20446337
机器学习“判定模型”和“生成模型”有什么区别?
重点
https://mp.weixin.qq.com/s/arAWD6_ipFWvNysNqumxmQ
判别模型和生成模型总结与对比:
20210511
判别:熟悉 湖畔大学
生成模型和判别模型的区别
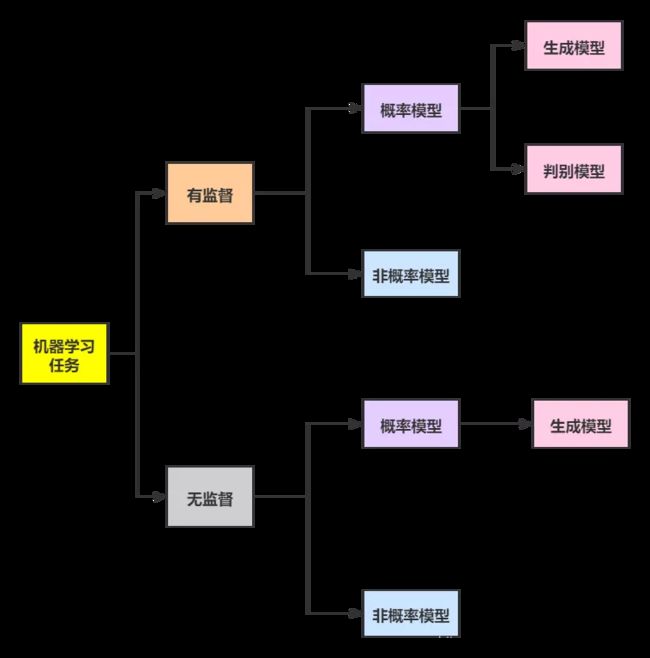
1.监督学习分为生成模型和判别模型
有监督机器学习方法可以分为生成方法和判别方法(常见的生成方法有混合高斯模型、朴素贝叶斯法和隐形马尔科夫模型等,常见的判别方法有SVM、LR等),生成方法学习出的是生成模型,判别方法学习出的是判别模型。 叛徒洛基(英雄)
2.生成模型
生成模型主要是求解联合概率密度,比如我们有数据集:(C,X),其中(c,x)表示其中一个样本,c为类别,x为特征。那么对于生成模型来说我们需要求解p(x,c)的联合概率密度,根据贝叶斯概率,p(x,c) = p(x|c)*p©,所以我们的任务变成了求解p(x|c)的类别条件概率,和p©的类别先验概率。
生成模型的求解思路是:联合分布——->求解类别先验概率和类别条件概率
3.判别模型
还是上面的例子,比如有了(C,X),其中(c,x)表示一个样本数据,c为类别,x为特征,那么判别模型输出的就是p(c|x)这个条件概率模型,即输入特征x,求输出类别是c的概率(c关于x的条件概率)。
实际上,这个过程包含了我们“看过”训练数据得到的后验知识,根据这个后验知识和测试集的特征就可以判断出测试集的类别。p(c|x) = p(c|x , C,X),我们认为这个条件概率由参数theta决定,即p(c|x, theta)。
但是theta怎样求得呢?theta是模型“看过”训练集后得到的,即theta在训练集上的后验分布p(theta | C,X)。
所以,综上整个流程为:p(c|x) = p(c|x, C,X) = p(c,theta|x,C,X)关于theta积分 = p(c|x , theta)*p(theta|C,X)关于theta积分。那么现在的重点就是求p(theta | C,X),即theta关于训练集的后验分布。
这个后验分布对应的似然函数为:p(C | X,theta) = L(theta) = 乘积p(c | x , theta)。
又因为贝叶斯概率:p(theta | C,X)*p(C | X) = p(C | X , theta)p(theta)。
又:p(C | X) = p(C,theta | X)对theta积分 = p(C | X , theta) p(theta)对theta积分。
综上:
![]()
条件分布——>模型参数后验概率最大——->(似然函数\cdot 参数先验)最大——->最大似然
4.生成模型和判别模型的优缺点
生成模型:
优点:
1)生成给出的是联合分布,不仅能够由联合分布计算条件分布(反之则不行),还可以给出其他信息,比如可以使用来计算边缘分布。如果一个输入样本的边缘分布很小的话,那么可以认为学习出的这个模型可能不太适合对这个样本进行分类,分类效果可能会不好,这也是所谓的outlier
detection。
2)生成模型收敛速度比较快,即当样本数量较多时,生成模型能更快地收敛于真实模型。
3)生成模型能够应付存在隐变量的情况,比如混合高斯模型就是含有隐变量的生成方法。
缺点:
1)天下没有免费午餐,联合分布是能提供更多的信息,但也需要更多的样本和更多计算,尤其是为了更准确估计类别条件分布,需要增加样本的数目,而且类别条件概率的许多信息是我们做分类用不到,因而如果我们只需要做分类任务,就浪费了计算资源。
2)另外,实践中多数情况下判别模型效果更好。
判别模型:
优点:
1)与生成模型缺点对应,首先是节省计算资源,另外,需要的样本数量也少于生成模型。
2)准确率往往较生成模型高。
3)由于直接学习,而不需要求解类别条件概率,所以允许我们对输入进行抽象(比如降维、构造等),从而能够简化学习问题。
缺点:
1)是没有生成模型的上述优点。
https://blog.csdn.net/algorithmPro/article/details/103625931
判别模型和生成模型总结与对比:
https://mp.weixin.qq.com/s/YwaNrjyUaMhS2r2FncuyMQ
理解生成模型与判别模型
https://mp.weixin.qq.com/s/J6XbAGyLE0toRZRMr5JfXg
https://mp.weixin.qq.com/s/xtx3ceq6GDO_h0iJcLAPag
机器学习基础 | 大话生成模型与判别模型
重点?
生成模型学习联合概率分布p(x,y),然后根据贝叶斯理论预测条件概率p(y|x),推导公式为:
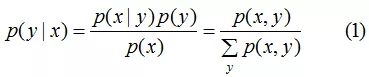
判别模型直接学习条件概率分布P(y|x)或学习决策函数y=f(x)预测输出。由(1)式可知生成模型可以得到判别模型,但判别模型得不到生成模型。
- 生成模型与判别模型的特点比较
生成模型是学习联合概率分布图片,然后利用贝叶斯理论去预测条件概率分布图片。生成模型明确的反映了数据集的分布情况,根据数据集的分布情况去预测测试数据的分类情况,当数据量较少时,学习到的联合概率分布图片与真实的联合概率分布图片差异较大,因此生成模型适合在数据量很大的情况,当模型需要考虑隐变量时,仍可用生成模型方法,此判别方法不能用。
判别模型是直接学习判别函数f(x)或条件概率分布p(y|x),它是根据训练数据不同类别之间的特征差异来学习决策边界,如支持向量机,逻辑斯蒂回归等模型。因此在数据量不多的情况下判别模型的分类结果要好于生成模型,但是判别模型不能反应数据集的真实分布情况。
8. 总结
生成模型和判别模型一般处理监督学习的问题,这两类模型都是通过预测条件概率分布p(y|x)进行分类(判别模型也可通过决策函数分类),只是方式不同:
生成模型思想:
学习联合概率分布p(x,y);
贝叶斯理论计算条件概率p(y|x);
判别模型思想:
直接通过训练数据估计条件概率分布P(y|x)或决策函数f(x);
生成模型的分类器:
朴素贝叶斯
贝叶斯网络
马尔科夫随机场
隐马尔可夫模型
判别模型的分类器:
逻辑斯蒂回归
支持向量机
最近邻算法
条件随机场