谣言检测文献阅读六—Tracing Fake-News Footprints: Characterizing Social Media Messages by How They Propagate
系列文章目录
- 谣言检测文献阅读一—A Review on Rumour Prediction and Veracity Assessment in Online Social Network
- 谣言检测文献阅读二—Earlier detection of rumors in online social networks using certainty‑factor‑based convolutional neural networks
- 谣言检测文献阅读三—The Future of False Information Detection on Social Media:New Perspectives and Trends
- 谣言检测文献阅读四—Reply-Aided Detection of Misinformation via Bayesian Deep Learning
- 谣言检测文献阅读五—Leveraging the Implicit Structure within Social Media for Emergent Rumor Detection
- 谣言检测文献阅读六—Tracing Fake-News Footprints: Characterizing Social Media Messages by How They Propagate
- 谣言检测文献阅读七—EANN: Event Adversarial Neural Networks for Multi-Modal Fake News Detection
- 谣言检测文献阅读八—Detecting breaking news rumors of emerging topics in social media
文章目录
- 系列文章目录
- 前言
- 1 介绍
- 2. 问题定义
- 3.提议的方法
-
- 3.1序列建模
- 3.2 用户嵌入
- 3.3 时间复杂度
- 4 算法-跟踪器
- 5.实验
-
- 5.1 数据集
- 5.2 实验设置
- 5.3 实验结果
-
- 社交媒体信息分类(四类)
- 虚假新闻检测
前言
文章:Tracing Fake-News Footprints:Characterizing Social Media Messages by How They Propagate
发表会议:WSDM (B类会议论文)
时间:2018年
1 介绍
消息可以是在社交网络上发布和转发的一条新闻、一个故事或一个表情包,而发布或转发它的用户就是传播者。消息的痕迹是指消息由谁以及何时传播,即发布或转发。
我们提出了 TraceMiner,这是一种使用扩散网络信息对社交媒体消息进行分类的新方法。 TraceMiner 将消息的跟踪作为输入并输出其类别。考虑到大量的社交媒体用户和所有可能的传播者组合,轨迹将是高维的,因此可能导致特征空间的稀疏性。为了解决这个问题,TraceMiner 利用社交网络中表现出的节点 [34] 和社交维度 [35] 的接近性,已成功应用于在无数应用程序中捕获社交媒体用户的内在特征
TraceMiner通过学习尚未充分利用的大量扩散数据,为社交媒体消息建模提供了另一种方法。现有的图挖掘研究主要集中在图和节点的学习表示上,而对节点间循环信息的分类研究较少。 TraceMiner通过直接建模信息并以端到端的方式进行预测,而不是仅提供属性向量或嵌入向量等方法和现有图形表示方法拉开距离。
本文的主要贡献有:
- 我们提出了一种利用扩散网络信息对社交媒体消息进行分类的新方法
- 我们推导出了有效的TraceMiner优化方法,并提供分析以保证正确性
- 我们在真实的社交网络数据上广泛地评估了性能,实验结果证明了在不同任务上的有效性。
2. 问题定义
我们考虑将社交媒体消息分为一个或多个类别的问题。我们定义了一个图 G ∈ < V , E > G∈
传统方法的问题定义:为了对消息进行预测,大多数现有方法将问题视为文本分类任务,因此,每个消息 m i m_i mi都有一组散布器 { ( v 1 m i , t 1 m i , c 1 m i ) , ⋅ ⋅ , ( v n m i , t n m i , c n m i ) } \{(v^{m_i}_1,t^{m_i}_1,c^{m_i}_1),··,(v^{m_i}_n,t^{m_i}_n,c^{m_i}_n)\} {(v1mi,t1mi,c1mi),⋅⋅,(vnmi,tnmi,cnmi)},其中 c j m i c^{m_i}_j cjmi是内容信息。
3.提议的方法
3.1序列建模
给定散布者信息 { ( v 1 m i , t 1 m i ) , ( v 2 m i , t 2 m i ) , ⋅ ⋅ ⋅ , ( v n m i , t n m i ) } \{(v^{m_i}_1,t^{m_i}_1),(v^{m_i}_2,t^{m_i}_2),···,(v^{m_i}_n,t^{m_i}_n)\} {(v1mi,t1mi),(v2mi,t2mi),⋅⋅⋅,(vnmi,tnmi)}和图G,可以通过图挖掘技术推断信息扩散的拓扑结构。拓扑结构通常是以初始散布器为根的树或林(多棵树),包含描述消息特征的信息模式。然而,直接处理树结构是极其困难的。考虑两条具有相似扩散网络的消息,添加或删除一个传播器,或者改变信息流的任何方向都会导致不同的树。从理论上讲,根据Cayley公式[7],有n个节点可能存在 n n − 2 n^{n−2} nn−2棵不同的树
为了解决这个问题,我们将树结构转换为时间序列。例如,给定 m i { ( v 1 m i , t 1 m i ) , ( v 2 m i , t 2 m i ) , ⋅ ⋅ ⋅ , ( v n m i , t n m i ) } m_i\{(v^{m_i}_1,t^{m_i}_1),(v^{m_i}_2,t^{m_i}_2),···,(v^{m_i}_n,t^{m_i}_n)\} mi{(v1mi,t1mi),(v2mi,t2mi),⋅⋅⋅,(vnmi,tnmi)}的扩展器,我们生成一个序列 x i = [ ( v q ( 1 ) m i , t q ( 1 ) m i ) , ⋅ ⋅ ⋅ , ( v q ( n ) m i , t q ( n ) m i ) ] x_i=[(v^{m_i}_{q(1)},t^{m_i}_{q(1)}),···,(v^{m_i}_{q(n)},t^{m_i}_{q(n)})] xi=[(vq(1)mi,tq(1)mi),⋅⋅⋅,(vq(n)mi,tq(n)mi)] 其中对于序列中的任意两个元素 k k k 和 j j j,如果 k < j k < j k<j,则 t q ( k ) m i < t q ( j ) m i t^{m_i}_{q(k)}< t^{m_i}_{q(j)} tq(k)mi<tq(j)mi,即 v q ( k ) m i v^{m_i}_{q(k)} vq(k)mi比 v q ( j ) m i v^{m_i}_{q(j)} vq(j)mi 更早地传播信息。因此,给定 n 个节点,所有可能的扩散网络的数量减少到 n ! n! n!。为了进一步缓解稀疏性,我们在第 3.2 节中加入了社会接近度和社会维度。
然而,对散布器按照时间排序的一个可能问题是用户之间的依赖性丢失,所以我们使用循环神经网络RNN。在信息传播中,发起传播过程的第一个传播者更有可能用于对消息进行分类。 因此,我们以相反的顺序馈送扩展序列,序列中的第一个扩展程序直接与预测结果交互,因此它具有更大的影响。在这项工作中,我们将隐藏节点的大小(k)设置为10。3.2节介绍了获取节点属性向量的方法。
选择LSTM RNN作为我们对消息进行分类的方法后,我们现在需要一种适合社交媒体用户的学习属性向量f的方法。一种直观的方法是利用社交网络图G生成嵌入向量,并将嵌入向量序列提供给LSTM RNN。我们遵循这一做法,因为 1) 几种社交图嵌入方法已被证明对分类任务有用,例如 LINE [34] 和 DeepWalk [29],以及 2) 用户出现在传播轨迹中遵循单词在社交中出现的类似分布媒体帖子。
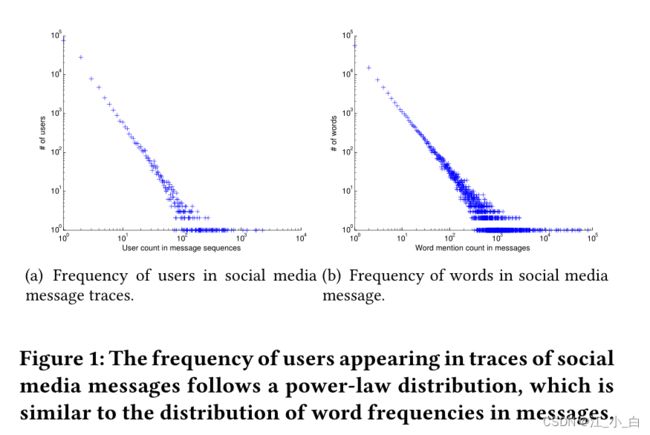
图1显示了用户和单词的分布。图1(a)中的分布来自真实世界的Twitter消息跟踪数据集,显示了用户在消息跟踪中的表现。图1(b)中的分布来自同一个数据集,显示了单词在消息内容中的显示方式。它们都遵循幂律分布,这促使我们将用户嵌入到低维向量中,就像在自然语言处理中如何使用单词的嵌入向量一样。
我们在算法 1 中展示了所提出的 LSTM-RNN 的训练。我们输入标记的传播器序列 X 和相应的标签 Y,它们在第 2 行中随机分为训练集和验证集。除了最大迭代次数 M a x i t e r Max_{it er} Maxiter,我们还有一个函数 EarlyStop() 用于控制训练的提前终止,它将验证集上的损失作为输入。在第 1 行中,我们使用高斯分布随机初始化模型参数。从第 3 行到第 7 行,我们用训练数据更新 W,直到达到最大 epoch 或满足提前终止条件。第 4 行中使用的损失函数如下所示:
 方程(1)计算了真实标签和预测之间的交叉熵。 ∣ Y t r = 0 ∣ ( ∣ Y t r = 1 ∣ ) |Y_{tr} = 0| (|Y_{tr} = 1|) ∣Ytr=0∣(∣Ytr=1∣)是训练集中负(正)实例的数量。由于我们的目标是进行多标签分类,当我们对其中一个进行建模时,数据自然是不平衡的,引入权重有助于模型平衡倾斜数据的梯度。在下一小节中,我们将介绍我们如何生成嵌入以及我们选择的原因。
方程(1)计算了真实标签和预测之间的交叉熵。 ∣ Y t r = 0 ∣ ( ∣ Y t r = 1 ∣ ) |Y_{tr} = 0| (|Y_{tr} = 1|) ∣Ytr=0∣(∣Ytr=1∣)是训练集中负(正)实例的数量。由于我们的目标是进行多标签分类,当我们对其中一个进行建模时,数据自然是不平衡的,引入权重有助于模型平衡倾斜数据的梯度。在下一小节中,我们将介绍我们如何生成嵌入以及我们选择的原因。

3.2 用户嵌入
评估了三种主流嵌入方法在一阶邻近度(互相连接,即互为好友)、二阶邻近度(有共同好友)以及社区近似度的效果,通过平均欧几里得距离评定。
 为了捕捉用户之间的社交接近度和社区相似度,我们提出了一个直接对这两种信息进行建模的原则框架。给定社交图 G,我们可以推导出邻接矩阵 S ∈ R n × n S ∈ R^{n×n} S∈Rn×n,其中 n 是用户数。我们的目标是学习一个转换矩阵 M ∈ R n × k M ∈ R^{n×k} M∈Rn×k,它将用户转换为维度为 k 的潜在空间。请注意,为了简洁起见,我们重用了 k,并且 LSTM-RNN 中的特征和隐藏节点的数量不一定相同。为了捕捉社区方面的相似性,我们引入了两个辅助矩阵,一个社区指示矩阵 H ∈ R n × g H ∈ R^{n×g} H∈Rn×g,其中 g 是社区的数量, t r ( H H T ) = n tr(HH^T ) = n tr(HHT)=n(每行只有一个元素为 1,其他元素均为 0) (tr(矩阵) 矩阵的迹,迹为矩阵对角线元素的和),以及社区表示矩阵 C ∈ R g × k C ∈ R^{g×k} C∈Rg×k ,其中每一行 c i c_i ci 是描述社区的嵌入向量。为了捕捉社区结构,我们将问题嵌入到属性社区检测模型中[44]:
为了捕捉用户之间的社交接近度和社区相似度,我们提出了一个直接对这两种信息进行建模的原则框架。给定社交图 G,我们可以推导出邻接矩阵 S ∈ R n × n S ∈ R^{n×n} S∈Rn×n,其中 n 是用户数。我们的目标是学习一个转换矩阵 M ∈ R n × k M ∈ R^{n×k} M∈Rn×k,它将用户转换为维度为 k 的潜在空间。请注意,为了简洁起见,我们重用了 k,并且 LSTM-RNN 中的特征和隐藏节点的数量不一定相同。为了捕捉社区方面的相似性,我们引入了两个辅助矩阵,一个社区指示矩阵 H ∈ R n × g H ∈ R^{n×g} H∈Rn×g,其中 g 是社区的数量, t r ( H H T ) = n tr(HH^T ) = n tr(HHT)=n(每行只有一个元素为 1,其他元素均为 0) (tr(矩阵) 矩阵的迹,迹为矩阵对角线元素的和),以及社区表示矩阵 C ∈ R g × k C ∈ R^{g×k} C∈Rg×k ,其中每一行 c i c_i ci 是描述社区的嵌入向量。为了捕捉社区结构,我们将问题嵌入到属性社区检测模型中[44]:

这里是将数据集中的用户构成了一个图,使用邻接矩阵表示,但是真实情况下,不能将所有用户作为一个图(G)
其中, s i M s_iM siM是嵌入向量,我们将其正则化为类似于其对应社区 h i C h_iC hiC的表示。第二项旨在通过预测用户和社区的嵌入向量分组来实现社区内的一致性[44]。等式(2)中的目标函数旨在使用嵌入向量对节点进行聚类。为了进一步将集群规范化为社会社区,我们采用了基于模块化最大化的方法,该方法已被广泛用于检测具有网络信息的社区[37]。具体来说,考虑到邻接矩阵S和社区成员指标,模块化定义如下[35]:
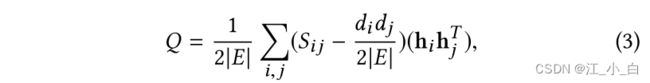 其中 ∣ E ∣ |E| ∣E∣是边的数目, d i d_i di是节点 i i i的度数。 h i h_i hi是节点 i i i的社区分配向量,如果 i i i和 j j j属于同一社区, h i h j T = 1 h_i h^T_j=1 hihjT=1,否则 h i h j T = 0 h_i h^T_j=0 hihjT=0。 d i d j 2 ∣ E ∣ \frac{d_id_j}{2 |E|} 2∣E∣didj是 i i i和 j j j之间的预期边数,如果边是随机放置的。模块化Q衡量社区内实际边数与随机放置的预期边数之间的差异。最优社区结构 H H H应通过定义模块化矩阵 B ∈ R n × n B∈ R_{n×n} B∈Rn×n使模块化 Q Q Q最大化,其中 B i j = S i j − d i d j 2 ∣ E ∣ B_{ij}=S_{ij}− \frac{d_id_j}{2 |E|} Bij=Sij−2∣E∣didj并抑制对模块化没有影响的常数,我们将公式(3)改写如下:
其中 ∣ E ∣ |E| ∣E∣是边的数目, d i d_i di是节点 i i i的度数。 h i h_i hi是节点 i i i的社区分配向量,如果 i i i和 j j j属于同一社区, h i h j T = 1 h_i h^T_j=1 hihjT=1,否则 h i h j T = 0 h_i h^T_j=0 hihjT=0。 d i d j 2 ∣ E ∣ \frac{d_id_j}{2 |E|} 2∣E∣didj是 i i i和 j j j之间的预期边数,如果边是随机放置的。模块化Q衡量社区内实际边数与随机放置的预期边数之间的差异。最优社区结构 H H H应通过定义模块化矩阵 B ∈ R n × n B∈ R_{n×n} B∈Rn×n使模块化 Q Q Q最大化,其中 B i j = S i j − d i d j 2 ∣ E ∣ B_{ij}=S_{ij}− \frac{d_id_j}{2 |E|} Bij=Sij−2∣E∣didj并抑制对模块化没有影响的常数,我们将公式(3)改写如下:
 为了保证嵌入向量在潜在空间中保持社区结构,我们建议将模块化最大化集成到嵌入方法中。目标函数可以用模块化最大化正则化器重写如下:
为了保证嵌入向量在潜在空间中保持社区结构,我们建议将模块化最大化集成到嵌入方法中。目标函数可以用模块化最大化正则化器重写如下:
 其中 β β β 控制社区结构的影响。如前所述,微观结构对于生成嵌入向量也至关重要。为了共同考虑细观和微观结构,我们将 M M M分解为全局模型参数 M ~ \tilde{M} M~和每个用户 i i i的局部变量 M i M_i Mi 的结合(每个用户 i i i的 M = M ~ + M i M = \tilde{M} +M_i M=M~+Mi)(推测 M i M_i Mi是M的第i维)。因此, M ~ \tilde{M} M~捕获了社区结构,而 M i M_i Mi可用于直接理解节点之间的微观结构。受近期网络正则化研究的启发,我们通过网络L1正则化项加强了具有邻近性的节点的表示:
其中 β β β 控制社区结构的影响。如前所述,微观结构对于生成嵌入向量也至关重要。为了共同考虑细观和微观结构,我们将 M M M分解为全局模型参数 M ~ \tilde{M} M~和每个用户 i i i的局部变量 M i M_i Mi 的结合(每个用户 i i i的 M = M ~ + M i M = \tilde{M} +M_i M=M~+Mi)(推测 M i M_i Mi是M的第i维)。因此, M ~ \tilde{M} M~捕获了社区结构,而 M i M_i Mi可用于直接理解节点之间的微观结构。受近期网络正则化研究的启发,我们通过网络L1正则化项加强了具有邻近性的节点的表示:
 其中 A ∈ R n × n A ∈ R^{n×n} A∈Rn×n是微观结构矩阵,如果我们的目标是在潜在空间中保持 i i i和 j j j之间的接近度,则 A i j = 1 A_{ij} = 1 Aij=1。遵循传统的图嵌入实践,我们考虑一级和二级接近度,这意味着如果 i 和 j 连接或共享一个共同的朋友,则 A i j = 1 A_{ij} = 1 Aij=1。当 Ai j = 1 时,对 M i 和 M j M_i 和 M_j Mi和Mj之间的差异施加 Frobenius 范数会激励它们相同。通过结合网络L2正则化器,目标函数可以重新表述如下:
其中 A ∈ R n × n A ∈ R^{n×n} A∈Rn×n是微观结构矩阵,如果我们的目标是在潜在空间中保持 i i i和 j j j之间的接近度,则 A i j = 1 A_{ij} = 1 Aij=1。遵循传统的图嵌入实践,我们考虑一级和二级接近度,这意味着如果 i 和 j 连接或共享一个共同的朋友,则 A i j = 1 A_{ij} = 1 Aij=1。当 Ai j = 1 时,对 M i 和 M j M_i 和 M_j Mi和Mj之间的差异施加 Frobenius 范数会激励它们相同。通过结合网络L2正则化器,目标函数可以重新表述如下:
 γ \gamma γ 是L2正则化系数。如我们所见,我们通过共同考虑社会群体和邻近性,在中观和微观网络结构之间建立共识关系。通过引入全局参数 M M M和个人变量 M i M_i Mi,我们迫使这两种信息都保留在新学习的嵌入向量中。然而,等式(5)并非对所有参数M、H和C都是联合凸的。为了解决该问题,我们将优化分为四个子问题,并对它们进行迭代优化。我们将在本节的其余部分介绍优化的细节。
γ \gamma γ 是L2正则化系数。如我们所见,我们通过共同考虑社会群体和邻近性,在中观和微观网络结构之间建立共识关系。通过引入全局参数 M M M和个人变量 M i M_i Mi,我们迫使这两种信息都保留在新学习的嵌入向量中。然而,等式(5)并非对所有参数M、H和C都是联合凸的。为了解决该问题,我们将优化分为四个子问题,并对它们进行迭代优化。我们将在本节的其余部分介绍优化的细节。
在修正 M i 、 H 和 C M_i、H和C Mi、H和C的同时更新 M ~ \tilde{M} M~:通过删除与 M ~ \tilde{M} M~无关的术语,我们得到以下优化问题:
 M ~ \tilde{M} M~采用如下更新方式:
M ~ \tilde{M} M~采用如下更新方式:
 其中 τ \tau τ是可以通过回溯线搜索获得的步长。 M ~ \tilde{M} M~的导数如下所示:
其中 τ \tau τ是可以通过回溯线搜索获得的步长。 M ~ \tilde{M} M~的导数如下所示:
 在固定 M ~ \tilde{M} M~、H 和 C 的同时更新 M i M_i Mi:通过删除与 M i M_i Mi无关的项,我们得到以下优化问题:
在固定 M ~ \tilde{M} M~、H 和 C 的同时更新 M i M_i Mi:通过删除与 M i M_i Mi无关的项,我们得到以下优化问题:
 对于 M i M_i Mi同样,我们推导出梯度:
对于 M i M_i Mi同样,我们推导出梯度:
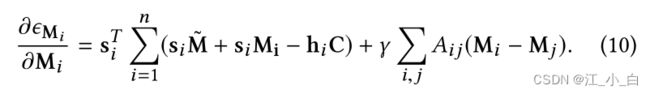 在固定 M ~ 、 M i \tilde{M}、M_i M~、Mi 和 H 的同时更新 C:通过删除与 C 无关的项,我们得到以下优化问题:
在固定 M ~ 、 M i \tilde{M}、M_i M~、Mi 和 H 的同时更新 C:通过删除与 C 无关的项,我们得到以下优化问题:
 C类似地,梯度可以得到:
C类似地,梯度可以得到:
 在固定 M ~ 、 M i \tilde{M}、M_i M~、Mi 和 C 的同时更新 H:通过删除与 H 无关的项,我们得到以下优化问题:
在固定 M ~ 、 M i \tilde{M}、M_i M~、Mi 和 C 的同时更新 H:通过删除与 H 无关的项,我们得到以下优化问题:
 其中 B ^ i j = d i d j 2 ∣ E ∣ \hat{B}_{ij} = \frac{d_id_j}{2 |E|} B^ij=2∣E∣didj .考虑到 H 是一个指示矩阵,约束使得方程(13)中的问题 NP 完全,这是极难解决的。为了解决这个问题,我们放宽对正交性 H T H = I H^TH = I HTH=I和非负性 H ≥ 0 H ≥ 0 H≥0的约束,并重新制定目标函数如下:
其中 B ^ i j = d i d j 2 ∣ E ∣ \hat{B}_{ij} = \frac{d_id_j}{2 |E|} B^ij=2∣E∣didj .考虑到 H 是一个指示矩阵,约束使得方程(13)中的问题 NP 完全,这是极难解决的。为了解决这个问题,我们放宽对正交性 H T H = I H^TH = I HTH=I和非负性 H ≥ 0 H ≥ 0 H≥0的约束,并重新制定目标函数如下:
 其中 λ > 0 λ > 0 λ>0应该是一个很大的数,以保证满足正交约束,我们在这项工作中将其设置为 108。然后,我们利用 ∣ ∣ X ∣ ∣ F 2 = t r ( X T X ) ||X||^2_F = tr(X^TX) ∣∣X∣∣F2=tr(XTX)的性质重新制定损失函数,如下所示:
其中 λ > 0 λ > 0 λ>0应该是一个很大的数,以保证满足正交约束,我们在这项工作中将其设置为 108。然后,我们利用 ∣ ∣ X ∣ ∣ F 2 = t r ( X T X ) ||X||^2_F = tr(X^TX) ∣∣X∣∣F2=tr(XTX)的性质重新制定损失函数,如下所示:
 其中 Θ = [ Θ i j ] Θ = [Θ_{ij} ] Θ=[Θij]是一个拉格朗日乘数矩阵,用于施加非负约束。将 ∂ ϵ H ∂ H \frac{{\partial^\epsilon }\textrm{H}}{\partial H} ∂H∂ϵH的导数设为0,我们有:
其中 Θ = [ Θ i j ] Θ = [Θ_{ij} ] Θ=[Θij]是一个拉格朗日乘数矩阵,用于施加非负约束。将 ∂ ϵ H ∂ H \frac{{\partial^\epsilon }\textrm{H}}{\partial H} ∂H∂ϵH的导数设为0,我们有:
 根据非负性的 Karush-Kuhn-Tucker (KKT) 条件,我们有如下等式:
根据非负性的 Karush-Kuhn-Tucker (KKT) 条件,我们有如下等式:
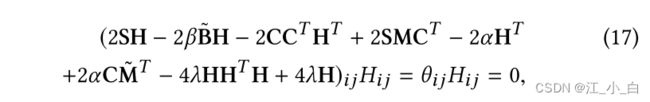 这是解在收敛时必须满足的不动点方程。 H 的更新规则可以写成:
这是解在收敛时必须满足的不动点方程。 H 的更新规则可以写成:

 ⨀ \bigodot ⨀ 同或运算 同1异0
⨀ \bigodot ⨀ 同或运算 同1异0
3.3 时间复杂度
TraceMiner 由两个组件组成,LSTM-RNN 和嵌入方法。虽然 LSTM-RNN 需要 O(|E| + |V |) 时间进行反向传播,但使用 Theano2 等深度学习软件库可以轻松提高可扩展性,尤其是在 GPU 可用时。由于用户数量通常远大于特征数量和社区数量,因此嵌入方法需要 O ( n 2 ) O(n^2) O(n2)时间。所有更新规则只使用矩阵乘法,因此可以通过使用像 OpenBLAS3 这样的矩阵优化库来加速优化。
4 算法-跟踪器
在本节中,我们将介绍 TraceMiner 方法进行网络扩散分类的详细过程。整个过程包括两个步骤:
- 基于网络连接学习嵌入。在这项工作中,我们的目标是利用用户的社会身份来推断她传播的信息。因此,我们从关联和社会社区成员中学习嵌入。
- 使用 LSTM-RNN 构建序列分类器。在我们获得社交媒体用户的嵌入后,我们将社交媒体消息视为其传播者的序列。我们使用 LSTM-RNN 对序列进行建模,并使用 softmax 聚合最终的隐藏输出以生成预测的类标签。
第一步利用网络结构将社交媒体用户嵌入到低维空间中,这缓解了利用社交媒体用户作为特征的数据稀疏性。第二步代表信息扩散的用户序列,允许对传播路径进行分类。
5.实验
在本节中,我们将介绍实验细节,以验证所提出框架的有效性。通过实验,我们的目标是回答两个问题:
- 与内容信息相比,网络信息在分类社交信息方面有多好
- 通过与提议的嵌入方法集成,LSTM RNN的有效性如何?
因此,我们使用真实数据集在两个不同的分类任务(分为真假 分为商业(b),科技(t),娱乐(e),医疗(m))上测试这些方法,并包括基于内容和基于网络的基线进行比较。
5.1 数据集
 数据集的统计信息如表 2 所示。我们收集了 3、600 条消息,其中 50% 是假新闻。其中,商业(b),科技(t),娱乐(e),医疗(m)。
数据集的统计信息如表 2 所示。我们收集了 3、600 条消息,其中 50% 是假新闻。其中,商业(b),科技(t),娱乐(e),医疗(m)。
5.2 实验设置
用F1评价模型好坏
 其中T是所有身份标签的集合, F 1 t F^t_1 F1t是任务 t t t 的 F 1 F_1 F1度量。
其中T是所有身份标签的集合, F 1 t F^t_1 F1t是任务 t t t 的 F 1 F_1 F1度量。
 M i c r o − F 1 Micro-F_1 Micro−F1等于Micro-precision and Micro-recall的调和平均数(调和平均数又称倒数平均数,是变量倒数的算术平均数的倒数)。
M i c r o − F 1 Micro-F_1 Micro−F1等于Micro-precision and Micro-recall的调和平均数(调和平均数又称倒数平均数,是变量倒数的算术平均数的倒数)。
5.3 实验结果
社交媒体信息分类(四类)
结果表明,当可用网络数据较少时,基于随机游走的方法可以产生更好的用户嵌入;当网络信息更加完整时,一种更具确定性的限制社交接近度的方法可以更好地理解用户行为。TraceMiner在所有任务中都能达到最佳效果。通过联合建模微观和介观结构,TraceMiner对数据稀疏性更具鲁棒性。
在训练信息较少的情况下,TM(DeepWalk)优于TM(LINE),而在信息更完整的情况下,TM(LINE)优于TM(DeepWalk)。在大多数情况下,TraceMiner仍然表现最好,直到我们将训练率提高到80%。XGBoost和TM(LINE)分别达到了80%和90%的最佳效果。这里有两个观察结果:随着更多的培训信息可用,1)建议的方法和基于内容的方法之间的差距变小;2)TraceMiner及其变体TM(LINE)和TM(DeepWalk)之间的差距变小。根据观察结果,我们可以得出结论,当可用的训练信息较少时,TraceMiner更有用,并且当已知的训练信息较少时,所提出的TraceMiner可以在学习的早期阶段很好地处理稀缺的数据。当80%的信息可用时,XGBoost将获得最佳效果。由于基于文本的分类是一个研究得很好的问题,而且当有丰富的信息可用时很容易解决,TraceMiner将能够补充那些基于内容的方法难以处理的情况,并且这些情况普遍存在于内容信息不足且嘈杂的社交媒体挖掘任务中。

虚假新闻检测
表4显示了不同方法在不同训练率(从10%到90%)的推特假新闻数据上的性能。由于数据集是平衡的,微观和宏观F1是相同的,因此只显示一组结果。对于基于内容的方法,XGBoost在所有情况下都始终优于SVM。对于TraceMiner的两种变体,观察到类似的模式:当可用的训练信息较少时,TM(DeepWalk)优于TM(LINE)。当有更多信息可供培训时,TM(LINE)优于TM(DeepWalk)。这再次证明了基于随机行走的采样对于稀缺数据更有效,基于邻近性的正则化可以更好地捕获具有更多训练信息的数据结构。
假新闻的结果与之前的实验之间的一个有趣差异是所提出的方法和基于内容的方法之间的差距更大。与内容信息更不言自明的新闻相关帖子不同,关于假新闻的帖子内容描述性较差。虚假新闻的故意传播者可能会操纵内容,使其看起来更类似于非谣言信息。因此,TraceMiner 可用于社交媒体中存在对抗性攻击的许多新兴任务,例如检测谣言和众筹。当更多信息可用于训练时,基于内容的方法和 TraceMiner 之间的差距变得更小,但是,在这些新兴任务中,获取训练信息通常是耗时且劳动密集型的。

当 10% 的信息可用时,SVM 的 F1 分数为 58%,略好于随机猜测,而 TraceMiner 的 F1 分数为 78%。虽然当有更多信息可用时,这种余量会减少,但在训练信息很少的情况下获得最佳性能对于强调早期的任务具有至关重要的意义。例如,在早期阶段检测假新闻比在 90% 的信息已知时检测它更有意义 [30,31,40]。