鲍鱼年龄预测

经典的线性回归模型主要用来预测一些存在着线性关系的数据集。回归模型可以理解为：存在一个点集，用一条曲线去拟合它分布的过程。如果拟合曲线是一条直线，则称为线性回归。如果是一条二次曲线，则被称为二次回归。线性回归是回归模型中最简单的一种。 本教程使用PaddlePaddle建立起一个鲍鱼年龄预测模型。

在线性回归中：
（1）假设函数是指，用数学的方法描述自变量和因变量之间的关系，它们之间可以是一个线性函数或非线性函数。 在本次线性回顾模型中，我们的假设函数为 Y’= wX+b ，其中，Y’表示模型的预测结果（预测的鲍鱼年龄），用来和真实的Y区分。模型要学习的参数即：w,b。

（2）损失函数是指，用数学的方法衡量假设函数预测结果与真实值之间的误差。这个差距越小预测越准确，而算法的任务就是使这个差距越来越小。 建立模型后，我们需要给模型一个优化目标，使得学到的参数能够让预测值Y’尽可能地接近真实值Y。这个实值通常用来反映模型误差的大小。不同问题场景下采用不同的损失函数。 对于线性模型来讲，最常用的损失函数就是均方误差（Mean Squared Error， MSE）。

（3）优化算法：神经网络的训练就是调整权重（参数）使得损失函数值尽可能得小，在训练过程中，将损失函数值逐渐收敛，得到一组使得神经网络拟合真实模型的权重（参数）。所以，优化算法的最终目标是找到损失函数的最小值。而这个寻找过程就是不断地微调变量w和b的值，一步一步地试出这个最小值。 常见的优化算法有随机梯度下降法（SGD）、Adam算法等等

# # **Step1.数据准备**
#
# **认识数据：**
#
#
# 数据集共4177行，每行9列
#
# 前8列用来描述鲍鱼的各种信息，分别是性别、长度、直径、高度、总重量、皮重、内脏重量、克重，最后一列为该鲍鱼的年龄
#
#
# **数据准备：**
#
# 1.从文件中加载数据
#
# 2.对数据进行归一化
#
# 3.构造数据集提供器


# 读取文件
import numpy as np
import os
import matplotlib.pyplot as plt

data_X = []
data_Y = []
# 将性别（M：雄性，F：雌性，I：未成年）映射成数字
sex_map = {'I': 0, 'M': 1, 'F': 2}
with open('data/data361/AbaloneAgePrediction.txt') as f:
    for line in f.readlines():
        line = line.split(',')
        line[0] = sex_map[line[0]]
        data_X.append(line[:-1])
        data_Y.append(line[-1:])
# 转换为nparray
data_X = np.array(data_X, dtype='float32')
data_Y = np.array(data_Y, dtype='float32')
# 检查大小
print('data shape', data_X.shape, data_Y.shape)
print('data_x shape[1]', data_X.shape[1])
# 归一化
for i in range(data_X.shape[1]):
    _min = np.min(data_X[:, i])  # 每一列的最小值
    _max = np.max(data_X[:, i])  # 每一列的最大值
    data_X[:, i] = (data_X[:, i] - _min) / (_max - _min)  # 归一化到0-1之间

import paddle
import paddle.fluid as fluid
from sklearn.model_selection import train_test_split

# 分割训练集、测试集
X_train, X_test, y_train, y_test = train_test_split(data_X,  # 被划分的样本特征集
                                                    data_Y,  # 被划分的样本标签
                                                    test_size=0.2,  # 测试集占比
                                                    random_state=0)  # 随机数种子，在需要重复试验的时候，保证得到一组一样的随机数


# 自定义reader,每次返回一个样本数据
def reader_creator(_X, _Y):
    def reader():
        for _x, _y in zip(_X, _Y):
            yield [_x, _y]  # 返回Iterable对象

    return reader


# 一个minibatch中有16个数据
BATCH_SIZE = 20

# 定义了用于训练与验证的数据提供器。提供器每次读入一个大小为BATCH_SIZE的数据批次。
# BATCH_SIZE个数据项组成一个mini batch。
train_reader = paddle.batch(reader_creator(X_train, y_train),
                            batch_size=BATCH_SIZE)
test_reader = paddle.batch(reader_creator(X_test, y_test),
                           batch_size=BATCH_SIZE)

# # **Step2.网络配置**
#
# **（1）网络搭建**：对于线性回归来讲，它就是一个从输入到输出的简单的全连接层。
#
# 对于鲍鱼年龄预测数据集，假设鲍鱼属性和年龄之间的关系可以被属性间的线性组合描述。

# 定义输入的形状和数据类型，张量变量x，表示8维的特征值
x = fluid.layers.data(name='x', shape=[8], dtype='float32')

# 定义输出的形状和数据类型，张量y,表示目标值
y = fluid.layers.data(name='y', shape=[1], dtype='float32')

# 定义一个简单的线性网络,连接输入和输出的全连接层
# input:输入;
# size:该层输出单元的数目
# act:激活函数
fc2 = fluid.layers.fc(input=x, size=200, bias_attr=True)
drop = fluid.layers.dropout(x=fc2, dropout_prob=0.5)
fc3 = fluid.layers.fc(input=drop, size=800, bias_attr=True, act='relu')
drop = fluid.layers.dropout(x=fc3, dropout_prob=0.5)
fc4 = fluid.layers.fc(input=drop, size=800, bias_attr=True, act='relu')
drop = fluid.layers.dropout(x=fc4, dropout_prob=0.5)
fc5 = fluid.layers.fc(input=drop, size=100, bias_attr=True, act='relu')
y_predict = fluid.layers.fc(input=fc5, size=1, bias_attr=True, act=None)

# **(2)定义损失函数**
#
# 此处使用均方差损失函数。
#
# square_error_cost(input,lable):接受输入预测值和目标值，并返回方差估计,即为（y-y_predict）的平方
cost = fluid.layers.square_error_cost(input=y_predict, label=y)  # 求方差
avg_cost = fluid.layers.mean(cost)  # 对方差求平均值，得到平均损失
# 克隆main_program得到test_program，使用参数for_test来区分该程序是用来训练还是用来测试，该api请在optimization之前使用.
test_program = fluid.default_main_program().clone(for_test=True)
# **(3)定义优化函数**

# 此处使用的是随机梯度下降。
optimizer = fluid.optimizer.AdamOptimizer(learning_rate=0.0001)
opts = optimizer.minimize(avg_cost)

# 完成上述定义，也就是完成了 fluid.default_main_program 的构建过程，fluid.default_main_program 中承载着神经网络模型，前向反向计算，以及优化算法对网络中可学习参数的更新。

# **fluid的设计思想：**
# 用户编写一段python程序，通过调用 Fluid 提供的算子，向一段 Program 中添加**变量**以及**对变量的操作**（Operators ）。
#
# 用户**只需要描述核心的前向计算**，不需要关心反向计算、分布式下以及异构设备下如何计算。
#
# Fluid 的 Program 的形式上类似一段 C++ 或 Java 程序。
#
# 包含：
#
# 1.本地变量的定义
#
# 2.一系列的operator
#
#
# **用户完成网络定义后，一段 Fluid 程序中通常存在 2 段 Program：**
#
# 1.**fluid.default_startup_program**：定义了创建模型参数，输入输出，以及模型中可学习参数的初始化等各种操作
#
# default_startup_program 可以由框架自动生成，使用时无需显示地创建
#
#
# 2.**fluid.default_main_program** ：定义了神经网络模型，前向反向计算，以及优化算法对网络中可学习参数的更新
#
# 使用Fluid的核心就是构建起 default_main_program

# # **Step3.网络训练 & Step4.网络评估**

# **（1）创建Executor**
#
# 首先定义运算场所 fluid.CPUPlace()和 fluid.CUDAPlace(0)分别表示运算场所为CPU和GPU
#
# Executor:接收传入的program，通过run()方法运行program。

# use_cuda为False,表示运算场所为CPU;use_cuda为True,表示运算场所为GPU
use_cuda = False
place = fluid.CUDAPlace(0) if use_cuda else fluid.CPUPlace()

# 创建一个Executor实例exe
exe = fluid.Executor(place)

# 正式进行网络训练前，需先执行参数初始化
exe.run(fluid.default_startup_program())

# **（2）定义输入数据维度**
#
# DataFeeder负责将数据提供器（train_reader,test_reader）返回的数据转成一种特殊的数据结构，使其可以输入到Executor中。
#
# feed_list设置向模型输入的向变量表或者变量表名

# In[ ]:


# 告知网络传入的数据分为两部分，第一部分是x值，第二部分是y值
feeder = fluid.DataFeeder(place=place, feed_list=[x, y])

# **（3）定义绘制训练过程的损失值变化趋势的方法draw_train_process**

# In[ ]:


iter = 0;
iters = []
train_costs = []


def draw_train_process(iters, train_costs):
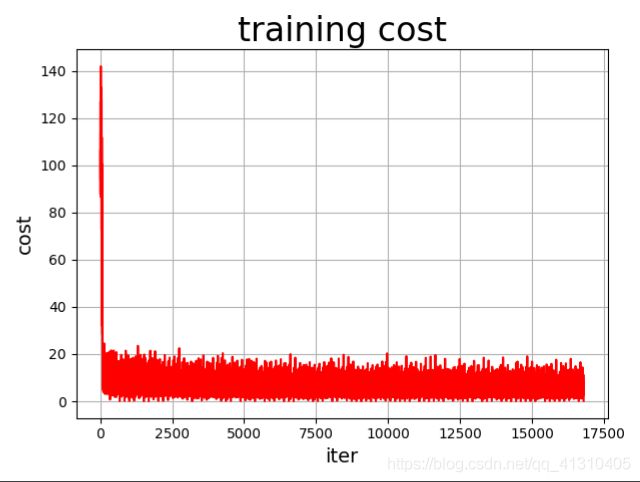
    title = "training cost"
    plt.title(title, fontsize=24)
    plt.xlabel("iter", fontsize=14)
    plt.ylabel("cost", fontsize=14)
    plt.plot(iters, train_costs, color='red', label='training cost')
    plt.grid()
    plt.show()


# **（4）训练并保存模型**
#
# Executor接收传入的program,并根据feed map(输入映射表)和fetch_list(结果获取表) 向program中添加feed operators(数据输入算子)和fetch operators（结果获取算子)。 feed map为该program提供输入数据。fetch_list提供program训练结束后用户预期的变量。
#
# 使用feed方式送入训练数据，先将reader数据转换为PaddlePaddle可识别的Tensor数据，传入执行器进行训练。
#
# 注：enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标

# In[ ]:


# 训练轮数：所有训练数据的一个前向传递和一个后向传递为一轮
EPOCH_NUM = 100
# 模型保存路径
model_save_dir = "/home/aistudio/work/fit_a_line.inference.model"

for pass_id in range(EPOCH_NUM):  # 训练EPOCH_NUM轮
    # 开始训练
    for batch_id, data in enumerate(train_reader()):  # 遍历train_reader迭代器
        train_cost = exe.run(program=fluid.default_main_program(),  # 运行主程序
                             feed=feeder.feed(data),  # 喂入一个batch的训练数据
                             fetch_list=[avg_cost])  # fetch 误差、准确率,fetch_list中设置要获取的值
        if batch_id % 100 == 0:
            print("Pass:%d, Cost:%0.5f" % (pass_id, train_cost[0]))  # 每训练100次，打印一次平均损失值

        iter = iter + 1
        iters.append(iter)
        train_costs.append(train_cost[0])

    # 开始验证，并输出验证集经过一轮的平均损失
    test_costs = []
    for batch_id, data in enumerate(test_reader()):  # 遍历test_reader迭代器
        test_cost = exe.run(program=test_program,  # 运行测试program
                            feed=feeder.feed(data),  # 喂入一个batch的测试数据
                            fetch_list=[avg_cost])  # fetch均方误差,fetch_list中设置要获取的值

        test_costs.append(test_cost[0])
    test_cost = (sum(test_costs) / len(test_costs))  # 每轮的平均误差
    print('Test:%d, Cost:%0.5f' % (pass_id, test_cost))  # 打印平均损失

    # 保存模型
    # 如果保存路径不存在就创建
if not os.path.exists(model_save_dir):
    os.makedirs(model_save_dir)
print('save models to %s' % (model_save_dir))

# 保存训练参数到指定路径中，构建一个专门用预测的program
fluid.io.save_inference_model(model_save_dir,  # 保存预测model的路径
                              ['x'],  # 预测需要 feed 的数据
                              [y_predict],  # 保存预测结果的变量
                              exe)  # exe 保存 inference model
# 绘制训练过程，损失随迭代次数的变化
draw_train_process(iters, train_costs)

# # **Step5.模型预测**
# **（1）创建预测用的Executor**

# In[ ]:


infer_exe = fluid.Executor(place)  # 创建推测用的executor
inference_scope = fluid.core.Scope()  # Scope指定作用域


# **（2）可视化真实值与预测值方法定义**
def draw_infer_result(groud_truths, infer_results):
    title = 'abalone'
    plt.title(title, fontsize=24)
    x = np.arange(1, 20)
    y = x
    plt.plot(x, y)
    plt.xlabel('ground truth', fontsize=14)
    plt.ylabel('infer result', fontsize=14)
    plt.scatter(groud_truths, infer_results, color='green', label='training cost')
    plt.grid()
    plt.show()


# **(3)开始预测**
#
# 通过fluid.io.load_inference_model，预测器会从params_dirname中读取已经训练好的模型，来对从未遇见过的数据进行预测。

with fluid.scope_guard(inference_scope):  # 修改全局/默认作用域（scope）, 运行时中的所有变量都将分配给新的scope。
    # 从指定目录中加载预测模型
    [inference_program,  # 预测用的program
     feed_target_names,  # 一个str列表，它包含需要在预测 Program 中提供数据的变量的名称。
     fetch_targets] = fluid.io.load_inference_model(  # fetch_targets: 从中可以得到预测结果。
        model_save_dir,  # model_save_dir:模型保存路径
        infer_exe)  # infer_exe: 预测用executor

    # 获取预测数据
    INFER_BATCH_SIZE = 10
    infer_reader = paddle.batch(reader_creator(X_test, y_test), batch_size=INFER_BATCH_SIZE)
    # 从infer_reader中分割x
    infer_data = next(infer_reader())
    infer_x = np.array([data[0] for data in infer_data]).astype("float32")
    infer_y = np.array([data[1] for data in infer_data]).astype("float32")

    results = infer_exe.run(inference_program,  # 预测模型
                            feed={feed_target_names[0]: np.array(infer_x)},  # 喂入要预测的x值
                            fetch_list=fetch_targets)  # 得到推测结果
    infer_results = []  # 预测值
    groud_truths = []  # 真实值
    sum_cost = 0
    for i in range(INFER_BATCH_SIZE):
        infer_result = results[0][i]  # 经过预测后的值
        ground_truth = infer_y[i]  # 真实值
        infer_results.append(infer_result)
        groud_truths.append(ground_truth)
        print("No.%d: infer result is %.2f,ground truth is %.2f" % (i, infer_result, ground_truth))
        cost = np.power(infer_result - ground_truth, 2)
        sum_cost += cost
    print("平均误差为:", sum_cost / INFER_BATCH_SIZE)

    draw_infer_result(groud_truths, infer_results)

结果：