【NeRF】基于Mindspore的NeRF实现
一、NeRF介绍
1. 背景
传统计算机图形学技术经过几十年发展,主要技术路线已经相对稳定。随着深度学习技术的发展,新兴的神经渲染技术给计算机图形学带来了新的机遇,受到了学界和工业界的广泛关注。神经渲染是深度网络合成图像的各类方法的总称,各类神经渲染的目标是实现图形渲染中建模和渲染的全部或部分的功能,基于神经辐射场(Neural Radiance Field, NeRF)的场景三维重建是近期神经渲染的热点方向,目标是使用神经网络实现新视角下的2D图像生成,在20和21年的CVPR、NeuIPS等各大AI顶会上,我们可以看到几十、上百篇相关的高水平论文。
2. 网络结构
NeRF使用多层感知机(Multilayer Perceptron,MLP)来重建三维场景,也就是去拟合空间点的颜色分布和光密度分布的函数。NeRF的网络结构如图1所示,网络的输入是采样点对应的空间坐标和视角,输出是采样点对应的密度和RGB值。
由于颜色\boldsymbol{c}c和光密度\sigmaσ在空间中并不是平滑的,变化是比较剧烈的,这意味着函数存在很多高频的部分,让模型去表示这种函数比较困难,所以NeRF通过positional encoding,对输入的\boldsymbol{r},\boldsymbol{d}r,d进行编码、升维,从而能够让模型更好地学出场景的一些细节部分,具体映射方式如下所示,该映射将标量pp映射成一个2L+12L+1维的向量:
\boldsymbol{\gamma}(p)=\left[p,\sin(2^0\pi p),\cos(2^0\pi p),\cdots,\sin(2^{L-1}\pi p), \cos(2^{L-1}\pi p)\right]γ(p)=[p,sin(20πp),cos(20πp),⋯,sin(2L−1πp),cos(2L−1πp)]
NeRF采用的MLP完整架构如下图所示:
3. 光线步进法
NeRF使用MLP隐式重建三维场景时的输入是采样点的位姿,NeRF的目标是实现2D新视角图像生成,那么要怎么得到采样点的位姿,又怎么使用重建得到的3D密度和颜色呢,得到新视角下的2D图像?
为了处理这两个问题,NeRF使用了光线步进(Ray Marching)这一经典方法,设\boldsymbol{o}o代表相机原点O_cOc在世界坐标系中的位置,\boldsymbol{d}d代表射线的单位方向矢量,tt代表从O_cOc出发,沿射线方向行进的距离。使用光线步进法时,2D图像的每个像素对应于一条射线,每条射线上的任意位置可以表示为\boldsymbol{r}(t)=\boldsymbol{o}+t\boldsymbol{d}r(t)=o+td,对这些射线进行采样(具体使用下文介绍的随机采样和重要性采样)即可得到采样点的位姿,对这些射线上的采样点进行积分(具体使用下文介绍的体绘制方法)即可得到2D像素的RGB值。
4. 随机采样和重要性采样
NeRF使用随机采样和重要性采样结合的方式在光线步进法生成的射线上进行采样,这是因为空间中的物体分布是稀疏的,一条射线上可能只有很小的一段区域是对最终渲染起作用的,如果用均匀采样会浪费很多采样点,网络也难以学到整个连续空间中的分布,所以采用coarse to fine的思想,构建粗采样网络和细采样网络可以更好的对空间进行采样。
随机采样:将射线从近场到远场的范围[t_n,t_f][tn,tf]均匀划分成N_cNc个区间,在每段区间内随机取一个点,将其空间坐标\boldsymbol{r}r和空间视角\boldsymbol{d}d输入粗采样网络,得到粗采样网络预测的该空间点的RGB\sigmaRGBσ。
重要性采样:粗采样网络的输出中包括一条射线上所有点的权重w_iwi(具体将在下一节解释),将其归一化后作为采样区间的概率密度函数PDF,按照概率密度函数随机采样N_fNf个点,与前面分段均匀采样的N_cNc个点合并后输入细采样网络。
NeRF将粗采样网络和细采样网络的渲染结果(2D像素点的RGB值),分别与ground truth计算均方误差,将两者之和作为总的loss,来同时训练两个网络。
5. 体绘制原理
得到采样点的密度和RGB值之后,NeRF使用计算机图形学中经典的体绘制技术(Voulume rendering)将3D采样值渲染至2D平面,具体原理如下。
光在介质中的衰减满足以下微分方程:
dL=-L\cdot \sigma \cdot dtdL=−L⋅σ⋅dt
其中LL为光强,\sigmaσ为衰减系数,其解为:
L=L_0\cdot \exp(-\int{\sigma}dt)L=L0⋅exp(−∫σdt)
假设:1) 空间点的颜色\boldsymbol{c}=[R,G,B]^Tc=[R,G,B]T和视线方向\boldsymbol{d}d有关;2) 空间点的光密度\sigmaσ和视线方向\boldsymbol{d}d无关。因为观察到的物体颜色会受到观察视角的影响(比如金属反射面),而光密度是由物体材质所决定。这一点假设也体现在了NeRF的网络结构当中。
根据光在介质中的衰减方程和体绘制原理,对于一个像素,其渲染颜色为
\boldsymbol{C}=\int_{t_{n}}^{t_{f}} T(t) \sigma(\boldsymbol{r}(t)) c(\boldsymbol{r}(t), \boldsymbol{d}) dtC=∫tntfT(t)σ(r(t))c(r(t),d)dt
其中,T(t)=\exp(-\int_{t_n}^{t}{\sigma(\boldsymbol{r}(s))}ds)T(t)=exp(−∫tntσ(r(s))ds)代表[t_n,t][tn,t]内的累积透光率,\sigma(\boldsymbol{r}(t))dtσ(r(t))dt代表距离微元dtdt内的光强衰减率,等效为\boldsymbol{r}(t)r(t)处的反射率。
再对积分式进行离散化处理,使之适于计算机处理:沿着射线取NN个点,在每个点ii所代表的区间长度\delta_iδi内,\sigma, \mathbf{c}σ,c视作常数,得到渲染得到的2D像素RGB值表达式为
\hat{C}(\mathbf{r})=\sum_{i=1}^{N}{T_i(1-\exp(-\sigma_i \delta_i))\mathbf{c_i}}C^(r)=i=1∑NTi(1−exp(−σiδi))ci
其中,累计透光率为T_i=\exp(-\sum_{j=1}^{i-1}\sigma_j \delta_j)Ti=exp(−∑j=1i−1σjδj)
用体绘制处理得到的2D像素RGB值,可用于计算loss,也可用于生成最终的2D新视角图像。同时,也可以得到如下两个量:
- \alpha_i=1-\exp(-\sigma_i \delta_i)αi=1−exp(−σiδi),为第ii个区间的不透明度。因此,T_i=\prod_{j=1}^{i-1}{(1-\alpha_i)}Ti=∏j=1i−1(1−αi),为前i-1i−1个区间的累积透明度;
- w_i=T_i\cdot \alpha_iwi=Ti⋅αi,为第ii个点的颜色对渲染颜色的贡献度,也就是权重,可用于计算粗采样网络得到的PDF。
6. NeRF的总体流程
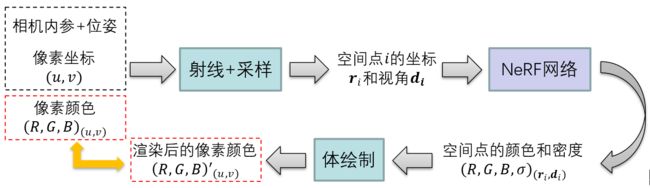
综上所述,NeRF实现场景新视角合成的工作流程如下图所示。
- 输入多视角图片(包括像素坐标、像素颜色),以及相机内参、位姿等数据;
- 根据光线步进法产生射线,用随机采样和重要性采样得到空间采样点的坐标;
- 将空间采样点的坐标以及射线的视角输入含有位置编码的NeRF,得到网络对于空间点RGB\sigmaRGBσ值的预测。
- 根据空间点的RGB\sigmaRGBσ值,用体绘制原理,渲染出射线对应的二维像素点的RGBRGB。
- 将预测、渲染得到的像素点的RGBRGB,与ground truth做MSE loss,训练神经网络。
二、代码流程介绍
项目地址:等算子完善后发布
程序实现环境:mindspore1.6.1+CUDA11.1。
整体实验流程:
1. 数据准备
NeRF的训练,除了对同一场景拍摄的多视角照片外,还需要相机的内参和每张照片的位姿。后者是无法通过直接测量得到的,因此需要使用一定的算法来获取。
COLMAP是一款通用的运动恢复结构 (SfM) 和多视图立体 (MVS) 软件,可用于点云重建。我们用COLMAP获取相机的内参和每张照片拍摄时的位姿,并根据3D特征点坐标,估计相机成像的深度范围,从而确定远、近平面,也就是边界。
操作步骤如下:
-
安装COLMAP,官方地址:https://demuc.de/colmap/
-
打开软件。点击File—New project,导入照片文件夹images,并在其所在目录下创建一个
database文件。 -
点击
Processing---Feature extraction,提取照片中的特征点。 -
点击
Processing---Feature matching,完成特征点匹配。 -
点击
Reconstruction---Start reconstruction,完成稀疏重建。 -
点击
Reconstruction---Dense reconstruction,点击Undistortion,输出稀疏重建的结果,包括相机内参、照片位姿、三维特征点信息的二进制文件。
COLMAP生成的数据为二进制文件,需要将数据重新保存成npy格式的文件poses_bounds.npy,便于后续数据的加载。操作步骤如下:
-
运行
img2pose.py文件,运行前需要配置形参为dense文件夹所在的目录。 -
运行后,在相应文件夹下生成
pose_bound.npy文件,数据预处理任务完成。pose_bound.npy文件内容:包含相机的内参、每幅图像的位姿(从相机坐标系到世界坐标系的变换矩阵),以及根据照片中的三维特征点信息计算出的每幅照片的成像深度范围。
此外,原始的拍摄照片像素数太多,无法进行计算,需要事先对图片进行下采样,减少计算量,此处采用8倍降采样。
2. 模型搭建
2.1 主干网络模块
首先是主干模型的搭建。模型输入:空间三维坐标在位置编码后的高维向量;模型输出:相应三维坐标点处的 的预测值。模型的具体架构参考原理部分。
这里需要注意模型权重的初始化,它对训练时收敛的快慢影响很大。这里,采用权重和偏置都在(-\sqrt{k},\sqrt{k})(−k,k)内均匀分布,其中k=1/\text{in-channels}k=1/in-channels,实测这种初始化方式对于NeRF的收敛是有帮助的。
class LinearReLU(nn.Cell):
def __init__(self, in_channels, out_channels):
super().__init__()
self.linear_relu = nn.SequentialCell([
nn.Dense(in_channels, out_channels,
weight_init=Uniform(-math.sqrt(1. / in_channels)),
bias_init=Uniform(-math.sqrt(1. / in_channels))),
nn.ReLU()
])
def construct(self, x):
return self.linear_relu(x)
class NeRF(nn.Cell):
def __init__(self, D=8, W=256, input_ch=3, input_ch_views=3, skips=[4], use_viewdirs=False):
super(NeRF, self).__init__()
self.D = D
self.W = W
self.input_ch = input_ch
self.input_ch_views = input_ch_views
self.skips = skips
self.use_viewdirs = use_viewdirs
self.pts_layers = nn.SequentialCell(
[LinearReLU(input_ch, W)] +
[LinearReLU(W, W) if i not in self.skips else LinearReLU(W + input_ch, W)
for i in range(D - 1)]
)
self.feature_layer = LinearReLU(W, W)
if use_viewdirs:
self.views_layer = LinearReLU(input_ch_views + W, W // 2)
else:
self.output_layer = LinearReLU(W, W // 2)
self.sigma_layer = nn.SequentialCell([
nn.Dense(W, 1,
weight_init=Uniform(-math.sqrt(1. / W)),
bias_init=Uniform(-math.sqrt(1. / W))) if use_viewdirs
else nn.Dense(W // 2, 1,
weight_init=Uniform(-math.sqrt(1. / (W // 2))),
bias_init=Uniform(-math.sqrt(1. / (W // 2)))),
])
self.rgb_layer = nn.SequentialCell(
nn.Dense(W // 2, 3,
weight_init=Uniform(-math.sqrt(1. / (W // 2))),
bias_init=Uniform(-math.sqrt(1. / (W // 2)))),
nn.Sigmoid()
)
def construct(self, x):
pts, views = mnp.split(x, [self.input_ch], axis=-1)
h = pts
for i, l in enumerate(self.pts_layers):
h = self.pts_layers(h)
if i in self.skips:
h = mnp.concatenate([pts, h], -1)
if self.use_viewdirs:
sigma = self.sigma_layer(h)
feature = self.feature_layer(h)
h = mnp.concatenate([feature, views], -1)
h = self.views_layer(h)
rgb = self.rgb_layer(h)
else:
h = self.feature_layer(h)
h = self.output_layer(h)
sigma = self.sigma_layer(h)
rgb = self.rgb_layer(h)
outputs = mnp.concatenate([rgb, sigma], -1)
return outputs
2.2 位置编码模块
位置编码需要将输入的三维坐标映射到高维,因此需要构建一个由\sin,\cossin,cos函数构成的列表。对于每个输入,进行编码函数的遍历,将输出结果拼接成高维。
class Embedder:
def __init__(self, **kwargs):
self.kwargs = kwargs
self.create_embedding_fn()
def create_embedding_fn(self):
embed_fns = []
d = self.kwargs['input_dims']
out_dim = 0
if self.kwargs['include_input']:
embed_fns.append(lambda x: x)
out_dim += d
max_freq = self.kwargs['max_freq_log2']
N_freqs = self.kwargs['num_freqs']
if self.kwargs['log_sampling']:
pow = ops.Pow()
freq_bands = pow(2., mnp.linspace(0., max_freq, N_freqs))
else:
freq_bands = mnp.linspace(2. ** 0., 2. ** max_freq, N_freqs)
for freq in freq_bands:
for p_fn in self.kwargs['periodic_fns']:
embed_fns.append(lambda x, p_fn=p_fn, freq=freq: p_fn(x * freq))
out_dim += d
self.embed_fns = embed_fns
self.out_dim = out_dim
def embed(self, inputs):
return mnp.concatenate([fn(inputs) for fn in self.embed_fns], -1)
def get_embedder(L):
embed_kwargs = {
'include_input': True,
'input_dims': 3,
'max_freq_log2': L - 1,
'num_freqs': L,
'log_sampling': True,
'periodic_fns': [mnp.sin, mnp.cos],
}
embedder_obj = Embedder(**embed_kwargs)
embed = lambda x, eo=embedder_obj: eo.embed(x)
return embed, embedder_obj.out_dim
2.3 损失网络
NeRF涉及到两个网络loss的相加后作为总的loss,来优化两个网络。因此,需要用NeRFWithLossCell类,将前向网络与损失函数连接起来。其中,前向计算过程比较复杂,涉及空间采样、位置编码、神经网络预测、体渲染等步骤,而这些步骤在测试阶段同样需要用到,因此将其封装成一个函数sample_and_render(),只需输入射线信息rays、网络信息net_kwargs、训练/测试的参数设置train_kwargs/test_kwargs,就能输出射线所对应像素点的RGB的预测值。
类的属性包括优化器、网络信息,还有打印信息所需psnr。psnr也是一个损失函数,但它不是优化的目标,因此不能作为construct的输出,只能用属性的方式进行记录。
class NeRFWithLossCell(nn.Cell):
def __init__(self, optimizer, net_coarse, net_fine, embed_fn_pts, embed_fn_views):
super(NeRFWithLossCell, self).__init__()
self.optimizer = optimizer
self.net_coarse = net_coarse
self.net_fine = net_fine
self.embed_fn_pts = embed_fn_pts
self.embed_fn_views = embed_fn_views
self.net_kwargs = {
'net_coarse': self.net_coarse,
'net_fine': self.net_fine,
'embed_fn_pts': self.embed_fn_pts,
'embed_fn_views': self.embed_fn_views
}
self.psnr = None
def construct(self, H, W, K, rays_batch, rgb, chunk=1024 * 32, c2w=None, ndc=True,
near=0., far=1., use_viewdirs=False, **kwargs):
# 数据准备,获取射线的位置、方向、远近场、视角
rays = get_rays_info(H, W, K, rays_batch, c2w, ndc, near, far, use_viewdirs=True)
# 采样+渲染
rets_coarse, rets_fine = sample_and_render(rays, **self.net_kwargs, **kwargs)
# 计算loss
loss_coarse = img2mse(rets_coarse['rgb_map'], rgb)
loss_fine = img2mse(rets_fine['rgb_map'], rgb)
loss = loss_coarse + loss_fine
self.psnr = mse2psnr(loss_coarse)
return loss
2.4 训练网络
这个类是封装损失网络和优化器,用优化器单步更新网络参数。
class NeRFTrainOneStepCell(nn.TrainOneStepCell):
def __init__(self, network, optimizer):
super(NeRFTrainOneStepCell, self).__init__(network, optimizer)
self.grad = ops.GradOperation(get_by_list=True)
self.optimizer = optimizer
def construct(self, H, W, K, rays_batch, rgb, **kwargs):
weights = self.weights
loss = self.network(H, W, K, rays_batch, rgb, **kwargs)
grads = self.grad(self.network, weights)(H, W, K, rays_batch, rgb, **kwargs)
return F.depend(loss, self.optimizer(grads))
3. 采样
3.1 粗采样
粗采样就是沿着射线进行分段均匀分布的随机采样。输入为射线和采样点数,以及其他参数配置,返回值为采样点的三维坐标pts、采样点在-z方向距离值z_vals,-z方向分段点z_splits。
def sample_coarse(rays, N_samples, perturb=1., lindisp=False, pytest=False):
N_rays = rays.shape[0]
rays_o, rays_d = rays[:, 0:3], rays[:, 3:6]
near, far = rays[..., 6:7], rays[..., 7:8]
t_vals = mnp.linspace(0, 1, N_samples + 1)
if not lindisp:
z_splits = near * (1. - t_vals) + far * t_vals
else:
z_splits = 1. / (1. / near * (1. - t_vals) + 1. / far * t_vals)
z_splits = mnp.broadcast_to(z_splits, (N_rays, N_samples + 1))
if perturb > 0.:
upper = z_splits[..., 1:]
lower = z_splits[..., :-1]
t_rand = np.random.rand(*list(upper.shape))
if pytest:
np.random.seed(0)
t_rand = np.random.rand(*list(z_splits.shape))
t_rand = Tensor(t_rand, dtype=ms.float32)
z_vals = lower + (upper - lower) * t_rand
else:
z_vals = .5 * (z_splits[..., 1:] + z_splits[..., :-1])
pts = rays_o[..., None, :] + rays_d[..., None, :] * z_vals[..., :, None]
return pts, z_vals, z_splits
3.2 细采样
细采样根据粗采样的得到的分段权重,将其作为概率密度函数进行采样,然后将采样结果和粗采样结果拼接,得到细采样输出。这里用sample_pdf()按照概率密度函数进行采样,其程序实现的主要步骤为:
- 根据PDF,计算累积分布函数CDF,它将是一个分段线性函数。
- 在[0, 1]内,对CDF值用均匀分布进行采样。
- 将采样到的CDF值映射回坐标值。
其中,第3步需要用高维的searchsorted算子去寻找坐标值的索引,然而,目前MindSpore的searchsorted只支持1维输入,无法完成这一任务,暂时用pytorch的算子代替。
def sample_pdf(bins, weights, N_samples, det=False, pytest=False):
weights = weights + 1e-5
pdf = weights / mnp.sum(weights, -1, keepdims=True)
cdf = mnp.cumsum(pdf, -1)
cdf = mnp.concatenate([mnp.zeros_like(cdf[..., :1]), cdf], -1)
if det:
u = mnp.linspace(0., 1., N_samples)
u = mnp.broadcast_to(u, tuple(cdf.shape[:-1]) + (N_samples,))
else:
u = np.random.randn(*(list(cdf.shape[:-1]) + [N_samples]))
u = Tensor(u, dtype=ms.float32)
if pytest:
np.random.seed(0)
new_shape = list(cdf.shape[:-1]) + [N_samples]
if det:
u = np.linspace(0., 1., N_samples)
u = np.broadcast_to(u, new_shape)
else:
u = np.random.rand(*new_shape)
u = Tensor(u, dtype=ms.float32)
cdf_tmp, u_tmp = torch.Tensor(cdf.asnumpy()), torch.Tensor(u.asnumpy())
inds = Tensor(torch.searchsorted(cdf_tmp, u_tmp, right=True).numpy())
below = ops.Cast()(mnp.stack([mnp.zeros_like(inds - 1), inds - 1], -1), ms.float32)
below = ops.Cast()(below.max(axis=-1), ms.int32)
above = ops.Cast()(mnp.stack([(cdf.shape[-1] - 1) * mnp.ones_like(inds), inds], -1), ms.float32)
above = ops.Cast()(above.min(axis=-1), ms.int32)
inds_g = mnp.stack([below, above], -1)
matched_shape = (inds_g.shape[0], inds_g.shape[1], cdf.shape[-1])
cdf_g = ops.GatherD()(mnp.broadcast_to(cdf.expand_dims(1), matched_shape), 2, inds_g)
bins_g = ops.GatherD()(mnp.broadcast_to(bins.expand_dims(1), matched_shape), 2, inds_g)
denom = (cdf_g[..., 1] - cdf_g[..., 0])
denom = mnp.where(denom < 1e-5, mnp.ones_like(denom), denom)
t = (u - cdf_g[..., 0]) / denom
samples = bins_g[..., 0] + t * (bins_g[..., 1] - bins_g[..., 0])
return samples
4. 射线获取
get_rays()完成的是根据照片尺寸[H,W][H,W]、相机内参矩阵KK,相机位姿c2wc2w,计算在世界坐标系下每个像素所对应的位置射线rays_o和方向射线rays_d。这里统一采用openGL坐标系,即xx为向右、yy为向上、zz为向外。其中,rays_d统一按照-z方向,也就是拍摄照片时相机的朝向,进行归一化。因为在进行粗采样和细采样时,对于所有不同方向的射线,都是以-z方向上的距离为准进行采样的。
get_rays_info()是将射线的所有信息拼接成rays张量,便于后续调用,射线信息包括:
- 位置向量rays_o;
- 方向向量rays_d;
- 近场near(体渲染时的积分下限);
- 远场far(体渲染时的积分上限);
- 单位化后的视角向量view_dir;
def get_rays(H, W, K, c2w):
i, j = mnp.meshgrid(mnp.linspace(0, W - 1, W), mnp.linspace(0, H - 1, H), indexing='xy')
dirs = mnp.stack([(i - K[0][2]) / K[0][0], -(j - K[1][2]) / K[1][1], -mnp.ones_like(i)], -1)
c2w = Tensor(c2w)
rays_d = mnp.sum(dirs[..., None, :] * c2w[:3, :3], -1)
rays_o = ops.BroadcastTo(rays_d.shape)(c2w[:3, -1])
return rays_o, rays_d
def get_rays_info(H, W, K, rays_batch=None, c2w=None, ndc=True, near=0, far=1, use_viewdirs=True):
if c2w is not None:
rays_o, rays_d = get_rays(H, W, K, c2w)
else:
rays_o, rays_d = rays_batch
if use_viewdirs:
viewdirs = rays_d
viewdirs = viewdirs / mnp.norm(viewdirs, axis=-1, keepdims=True)
viewdirs = mnp.reshape(viewdirs, [-1, 3])
if ndc:
rays_o, rays_d = ndc_rays(H, W, K[0][0], 1., rays_o, rays_d)
rays_o = mnp.reshape(rays_o, [-1, 3])
rays_d = mnp.reshape(rays_d, [-1, 3])
near, far = near * mnp.ones_like(rays_d[..., :1]), far * mnp.ones_like(rays_d[..., :1])
rays = mnp.concatenate([rays_o, rays_d, near, far], -1)
if use_viewdirs:
rays = mnp.concatenate([rays, viewdirs], -1)
return rays
5. 渲染
根据网络输出的空间采样点的RGB\sigmaRGBσ,用体渲染公式计算出射线对应二维像素点的RGB值。因此,本函数是NeRF前向计算的主体框架。其主要过程为:
- 根据射线数据,进行粗采样。
- 将粗采样得到的空间采样点坐标
pts_coarse,和射线单位方向向量views_coarse拼接,输入粗采样网络。经过位置编码和神经网络前向计算,得到空间采样点RGB\sigmaRGBσ预测值raw_coarse。其中,views_coarse是rays_d的单位向量,消除了不同向量模长的影响。 - 将
raw_coarse输入体绘制函数render(),得到渲染后的返回值ret_coarse。它是一个字典,包括了渲染后的所有结果,其中包括粗采样点的权重rets_coarse['weights']。 - 根据粗采样网络采样点的权重,以及采样分段区间,进行细采样。
- 将细采样得到的空间采样点坐标
pts_fine,和射线单位方向向量views_fine拼接,输入细采样网络。经过位置编码和神经网络前向计算,得到空间采样点RGB\sigmaRGBσ预测值raw_fine。 - 将
raw_fine输入体绘制函数render(),得到渲染后的返回值ret_fine,它同样包括了渲染后的所有结果。 - 返回粗采样网络和细采样网络渲染后的返回值
rets_coarse,rets_fine。
def sample_and_render(rays, net_coarse=None, net_fine=None, embed_fn_pts=None, embed_fn_views=None, N_coarse=64, N_fine=64, perturb=1., lindisp=False, pytest=False, raw_noise_std=0., white_bkgd=False):
# 数据准备
rays_d = rays[..., 3: 6]
views = rays[:, -3:] if rays.shape[-1] > 8 else None
# 粗采样
pts_coarse, z_coarse, z_splits = sample_coarse(rays, N_coarse, perturb, lindisp, pytest)
views_coarse = mnp.broadcast_to(views[..., None, :], pts_coarse.shape)
sh = pts_coarse.shape
# 粗采样网络的positional encoding
pts_embeded_coarse = embed_fn_pts(pts_coarse.reshape([-1, 3]))
views_coarse_embeded = embed_fn_views(views_coarse.reshape([-1, 3]))
# 输入粗采样网络 + 渲染 得到输出
net_coarse_input = mnp.concatenate([pts_embeded_coarse, views_coarse_embeded], -1)
raw_coarse = net_coarse(net_coarse_input).reshape(list(sh[:-1]) + [4])
rets_coarse = render(raw_coarse, z_coarse, rays_d,
raw_noise_std, white_bkgd, pytest)
# 细采样
weights = rets_coarse['weights']
pts_fine, z_fine = sample_fine(rays, z_coarse, z_splits, weights,
N_fine, perturb, pytest)
views_fine = mnp.broadcast_to(views[..., None, :], pts_fine.shape)
sh = pts_fine.shape
# 细采样网络的positional encoding
pts_embeded_fine = embed_fn_pts(pts_fine.reshape([-1, 3]))
views_embeded_fine = embed_fn_views(views_fine.reshape([-1, 3]))
# 输入细采样网络 + 渲染 得到输出
net_fine_input = mnp.concatenate([pts_embeded_fine, views_embeded_fine], -1)
raw_fine = net_fine(net_fine_input).reshape(list(sh[:-1]) + [4])
rets_fine = render(raw_fine, z_fine, rays_d,
raw_noise_std, white_bkgd, pytest)
return rets_coarse, rets_fine
6. 主函数
main函数的任务如下:
- 加载图片和位姿、内参等数据,将其分成一个一个batch并打乱;
- 用
create_nerf(),创建一个NeRF模型,返回值包括:各网络实例构成的字典net_kwargs,训练参数train_kwargs,测试参数test_kwargs,优化器optimizer。 - 构建损失网络
net_with_loss,并加载之前保存的训练参数。 - 构建训练网络
train_net。 - 迭代优化
train_net。 - 保存训练时参数,保存渲染视频。
训练时调用训练网络:
train_net(H, W, K, batch_rays, target_s, **train_kwargs)
三、参考资料
[1] Mildenhall, B., Srinivasan, P.P., Tancik, M., Barron, J.T., Ramamoorthi, R., Ng, R. (2020). NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. In: Vedaldi, A., Bischof, H., Brox, T., Frahm, JM. (eds) Computer Vision – ECCV 2020. ECCV 2020.
[2] NeRF论文的官方实现: GitHub - bmild/nerf: Code release for NeRF (Neural Radiance Fields)
[3] NeRF的Pytorch实现:GitHub - yenchenlin/nerf-pytorch: A PyTorch implementation of NeRF (Neural Radiance Fields) that reproduces the results.
[4] MindSpore 1.6 API:MindSpore API — MindSpore master documentation