[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for
⭐️Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for Traffic Flow Prediction
原文链接,见这里
作者:Kun Yu,Xizhong Qin *,Zhenhong Jia,Yan Du andMengmeng Lin
期刊:MDPI ,Sensors
关键字:交通流预测;数据多样性;交叉注意;时空多图
相关阅读博文:《阅读笔记》
data code:《CAFGCN》,只有数据没有代码
文章目录
- :star:Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for Traffic Flow Prediction
-
- 摘要
- 1. Introduction
- 2. Related Work
-
- 2.1. T raffic Flow Prediction
- 2.2. Multi-Graph Convolutional Networks
- 2.3. Cross-Attention Mechanism
- 3. Preliminaries
- 4. Methodology
-
- 4.1. Multi-Level Temporal Inputs
- 4.2. Multi-Graph Convolutional Layer
-
- 4.2.1. Multi-Graph Construction
- 4.2.2. Multi-Graph Convolutional Network
- 4.3. Cross-Attention Mechanism Fusion
-
- 4.3.1. Cross Attention
- 4.3.2. Feature Fusion
- 5. Experiment
-
- 5.1. Datasets Description
- 5.2. Settings
- 5.3. Baselines
- 5.4. Evaluation Metric
- 5.5. Experiment Results Analysis
- 5.6. Ablation Experiment
- 6. Conclusions and Outlook
- References
摘要
准确的交通流预测对于建设智慧交通城市至关重要。现有的研究主要采用给定的单一图结构作为模型,只考虑局部和静态的空间依赖关系,忽略了动态时空数据多样性的影响。为了充分捕捉时空数据多样性的特点,提出了一种基于交叉注意融合的时空多图卷积网络(CAFMGCN) a cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network (CAFMGCN) mode交通流预测模型。首先,引入GCN对历史交通数据的三个时间属性(当前、每日和每周)进行建模,以提取时间特征。其次,考虑距离和交通流之间的关系,构建邻接图、连通图和区域相似图来获取动态空间拓扑信息。为了充分利用全局信息,引入交叉注意机制 a cross-attention mechanism,分别融合时间和空间特征,以减少预测误差。最后,对 CAFMGCN 模型进行了评价,实验结果表明,该模型的预测比其他模型的基线预测更准确有效。
1. Introduction
在智能交通城市中,交通流预测越来越受到人们的重视。近年来,随着经济的快速增长和城市车辆数量的增加,许多城市的交通拥堵和交通事故日益困扰,给出行带来了许多不便。人们都希望通过建设智慧交通城市来缓解交通拥堵,提高交通管理效率。智能交通系统(ITS)被广泛应用于改善交通状况[1,2]。
交通流预测的相关研究已有近40年的历史,已有数十种预测方法被提出。城市道路交通流量根据预测时间分为长期预测、中长期预测和短期预测。研究方法分为经典时间序列预测方法、传统机器学习方法和深度学习方法,从经典时间序列模型如历史平均(HA)[4]和自回归综合移动平均(ARIMA)[5],到传统的机器学习模型如支持向量机回归(SVR)[6]。虽然它们可以很好地捕捉到时间相关性,但它们忽略了空间相关性的重要性。直到深度学习模型的出现,这个问题才得以解决。在早期,研究人员主要使用RNN(递归神经网络)来解决空间相关性问题,如LSTM(长短期记忆)[7,8]和GRU(门控递归单元)[9,10]模型。虽然基于rnn的方法可以学习空间相关性,但它们往往过于复杂,无法处理非线性相关性。此外,传统的深度学习方法很容易与时空相关性分离,使用单独的模块实现时间和空间相关性[11]。
最近,图卷积神经网络(GCN)已成为交通预测问题中最热门的话题[12,13]。与传统的数据驱动方法不同,图神经网络可以处理非欧几里德数据并捕获道路拓扑信息。与其他方法相比,训练速度更快,参数也有所减少。如图1所示,在交叉口处形成道路网。当一个路段发生拥堵时,其相邻路段将受到显著影响,并在一定时期内扩散到其他路段。以节点1为目标节点,当节点1发生拥塞时,相邻节点2的相关性较强,而相邻节点5的相关性较弱。与远端节点3和节点4相比,它们都具有特定的相关性。因此,可以看出,交通路段之间的网络空间相关性相当复杂。地理位置相似的两个路段之间的交通条件可能不相关,但距离较长的两个路段之间的交通条件可以连接。此外,不同时间观测值之间也存在特定的非线性相关性。同一节点在不同时间(例如一小时前、一天前、甚至一周前)的不同观测值与测量点相关。要做到这一点,我们必须将这些信息纳入模型中,以做出准确的交通预测。图2是模拟道路流量相关性的示例.
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第1张图片](http://img.e-com-net.com/image/info8/06bcf4ddc90841809d19c3ebd89572e9.jpg)
我们提出了一种新的时空融合模型来解决上述问题,称为交叉注意融合多图卷积网络(CAFMGCN)。该模型使用 MCGN 和 时空交叉注意机制 spatio-temporal cross-attention mechanism 来研究基于图形视角的多变量时间序列数据。多图卷积有两个功能:一个是构造具有三种不同时间属性的相关图来捕获时间特征;另一种是构建三条不同道路之间的空间语义关联图,以获取空间特征。输入层将当前、每日和每周三个不同时段的历史交通流作为输入。我们使用三个时态图来表示不同时期的节点特征,以捕获多级时间相关性。对于卷积层,我们提出了一种多图卷积网络来捕获不同节点之间的空间相关性,并构造了三个邻接图来表示不同类型的节点关系特征,以捕获空间相关性和全局信息。为了同时捕获输出层中的时空相关特征,我们使用交叉注意机制对构建的时空图进行多图融合,以减少数据丢失。本文的主要贡献如下:
- 提出了一种新的多图网络模型体系结构,它分别处理多级时间相关性(即当前、每日和每周)和多空间位置相关性(即邻近性、连通性和区域相似性)。建模用于捕获不同时间不同位置节点的时间和空间特征。
- 提出了一种新的时空融合方法&时空交叉注意融合机制。该机制可以同时捕获时空特征并进行整体融合,有效减少了捕获特征图时的计算量和数据丢失。
- 在两个真实的交通数据集上进行了广泛的实验。结果表明,与现有基线相比,CAFMGCN模型具有更好的可预测性。
2. Related Work
本节回顾了与交通流预测相关的图卷积网络和时空交叉注意的最新研究,并指出了以往研究的局限性。
2.1. T raffic Flow Prediction
近年来,交通流预测的研究取得了许多优秀的成果。用于交通流预测的模型已经从最初的传统时间统计模型发展到现在的深度学习模型。随着深度学习在语音识别[14]、图像分类[15]等领域取得的诸多突破,越来越多的研究人员将深度学习应用于时空数据预测。例如
文献[16]使用递归神经网络(RNN)和卷积神经网络(CNN)对交通速度进行建模,捕捉时间和空间相关性。
文献[17]提出了一种结合CNN和LSTM的方法,来模拟交通流的变化状态,利用道路之间的相互作用来捕捉空间相关性。
文献[18]引入了3D卷积,自动获取交通数据在时空维度上的相关性。
现有的这些方法虽然可以从交通网络的邻域提取空间特征,但往往忽略了道路的物理特征(如长度和限速)。它们不足以获取全面的路网信息。此外,大多数RNN/CNN模型都是基于欧几里得结构来进行预测。他们很少挖掘非欧几里得拓扑结构的网络,因此在本质上不能表征道路的空间相关性。
2.2. Multi-Graph Convolutional Networks
图卷积网络的应用
图卷积网络是一种新兴的深度学习模型,可以很好地处理非欧几里德空间数据,并已应用于道路网络的空间建模。
文献[19]提出了扩散卷积递归神经网络Diffusion Convolutional Recursive Neural Network(DCRNN),该网络将交通流建模为有向图上的扩散过程,并引入双向有向图来考虑空间相关性。
文献[20]使用图卷积和门卷积的组合combination of graph convolution and gated convolution 来捕获时空相关性。
由于交通数据是不断变化的,在以前的GCN方法中,图结构的定义通常是局部的和静态的,没有考虑交通数据的动态特性。因此,
文献[21]设计了一个自适应矩阵adaptive matrix ,以考虑节点及其邻居之间影响的变化。
文献[22]使用动态拉普拉斯矩阵dynamic Laplacian matrix估计器来跟踪交通数据之间的空间变化。
文献[23]设计了注意图卷积序列到序列framework of the Attention Graph Convolution Sequence-to-Sequence(AGC-Seq2Seq)模型的框架,以多步预测方法捕获交通模式的时空变化。
然而,时空网络数据通常在空间和时间维度上都表现出异质性。例如,在城市道路网中,住宅区和商业区交通监测站记录的观测结果通常在不同时间显示不同的模式【24】。基于单个GCN无法提取时空拓扑信息。
多图卷积网络的应用
多图网络模型用于共享自行车预测【25】和叫车需求预测【26】,但很少用于道路交通流预测。文献[27,28]通过测试周期与当前、每日和每周周期之间的关系,对时间多样性进行建模。为了捕捉长距离时空异质性,
文献[29]设计了不同时期的多模块建模。 —>
对用不同时期
文献[30]介绍了多图GCN来分别处理三种流入和流出模式(当前、每日和每周),并使用了不同流入和流出模式之间以及附近和远处站点之间的高级时空特征,这些特征可以通过3D CNN提取。 —>对应不同模式?
文献[31]使用多图网络为节点邻接、连通性和功能性的不同属性构建邻接矩阵,以测量道路之间的空间相关性。 —>对应不同该矩阵
这些模型能够很好地提取时间和空间特征。然而,它们往往将时空相关性分离开来,无法同时捕获多层次的时间相关性和异质空间相关性。
2.3. Cross-Attention Mechanism
注意机制是基于编码器/解码器模型实现的。该模型最初用于机器翻译[32],
后来的文献[33,34]在交通流预测中引入了软注意和硬注意机制。利用注意机制捕获道路网络动态变化的时空相关性,较好地捕获全局时间信息和空间相关性。
文献[35]将自我注意引入了生成性对抗网络 generative adversarial network,并取得了很好的实验结果。
文献[36]首次将交叉注意模块引入图像检测 image detection,考虑到远距离对上下文信息的影响。它使用了一种更有效的方法来捕获远程时间上下文信息。
文献[37]提出了一种基于交叉注意融合的增强图卷积网络an enhanced graph convolutional network based on cross-attention fusion,用于深度聚类。
文献[38]将交叉注意力cross-attention 用于救护车需求预测。交叉注意机制不仅训练速度快,而且只占用很少的GPU。
本文提出了一种用于交通流预测的多图卷积和交叉注意融合机制,以更好地解决道路网络中多层时间和异构空间相关性问题。
3. Preliminaries
在本节中,我们定义了道路交通网络建模的基本概念,并说明了存在的问题。
Definition 1. T raffic Road Graph
在时间上,我们将历史时段划分为一组连续的时间片,记为 T = { h t ∣ t ∈ 1 , 2 , ⋅ ⋅ ⋅ , T } T=\{h_t|t∈1,2,⋅⋅⋅,T\} T={ht∣t∈1,2,⋅⋅⋅,T}。每个节点在每个时间片上生成一个特征向量。本文使用三个历史时间片段(当前、每日和每周)的特征图作为输入信息,具体内容在4.1节中详细阐述。
在空间上,我们将道路图表示为加权图 G = ( V , E , A ) G=(V,E,A) G=(V,E,A),其中 V = { v i ∣ i ∈ 1 , 2 , ⋅ ⋅ ⋅ , N } V=\{v_i | i∈1,2,⋅⋅⋅,N\} V={vi∣i∈1,2,⋅⋅⋅,N} 是一组N个检测器节点,每个节点 v i v_i vi代表一个检测器。 E E E是连接这些节点的一组边,每条边 e i j e_{ij} eij表示 v i v_i vi和 v j v_j vj之间的相关性。边 e i j e_{ij} eij的权重表示 v i v_i vi和 v j v_j vj之间的相关强度。权重越大,两条道路之间的相关性越高。 A ∈ R N × N A∈R^{N×N} A∈RN×N是图 G G G的邻接矩阵。本文从三个方面构建道路图:道路网络拓扑( X w X_w Xw)、交通连通性( X P X_P XP)和区域相似性( X s X_s Xs),这将在第4.2.1节中详细阐述。
Definition 2. Problem Definition.
我们使用 x t c , i x^{c,i}_t xtc,i,它表示节点 i i i在时间 t t t的第 c c c个特征, X t i X^i_t Xti表示节点 i i i在时间 t t t的所有特征值, X t X_t Xt表示时间t的所有节点的所有特征值。 X = ( X 1 , X 2 , ⋅ ⋅ ⋅ , X τ X=(X_1,X_2,⋅⋅⋅,X_{\tau} X=(X1,X2,⋅⋅⋅,Xτ表示τ时间片上所有节点的所有特征值。根据各种历史观察结果, X i n p u t { X t − τ ∣ τ ∈ ( 0 , 1 , ⋅ ⋅ ⋅ , w − 1 ) } X_{input}\{X_{t−\tau}|\tau∈(0,1,⋅⋅⋅,w−1) \} Xinput{Xt−τ∣τ∈(0,1,⋅⋅⋅,w−1)}在过去的 w w w个时间片中,在 X w X_w Xw、 X P X_P XP和 X s X_s Xs的前提下,利用多图网络的模型知识学习函数f。交通流预测问题旨在预测下一时刻 X ^ t \hat{X}_t X^t的交通量。即:

4. Methodology
我们的CAFMGCN模型如图3所示。该模型由多级时间输入、多图卷积层和时空交叉注意融合模块组成。
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第3张图片](http://img.e-com-net.com/image/info8/48ecc91b5eb34fa3a1ff9334359ffb59.jpg)
4.1. Multi-Level Temporal Inputs
根据文献[18,27,28,30],待测周期与其当前、每日和每周周期之间有很强的相关性。为了充分捕捉时间维度的特征,本文根据时间序列将当前、每日和每周待测时段组合在时间维度上作为模型的输入,以此表示多层次的时间相关性。
首先,将一天平均划分为 q q q个时段,我们以当前时刻 t t t为起点;预测窗口大小为 p p p。分别使用 X r X_r Xr、 X d X_d Xd和 X w X_w Xw表示待测期间当前、每日和每周模式的时间维度特征图,然后:
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第4张图片](http://img.e-com-net.com/image/info8/475a8ab3fd504a66b72fabd2e751a7a2.jpg)
where, T r T_r Tr、 T d T_d Td和 T w T_w Tw表示最新时段、每日时段和每周时段的长度。由三种时态拼接而成的并集用作模型的输入集:
![]()
其中, d d d和 w w w表示每日和每周时间段中的时间片数(例如,在1小时时间段中, d = 24 d=24 d=24, w = 24 × 7 w=24×7 w=24×7), l r l_r lr、 l d l_d ld和 l w l_w lw分别为3、1和1。模型输入如图4所示。
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第5张图片](http://img.e-com-net.com/image/info8/72beb6f70f4743b28743f145ff941a7a.jpg)
4.2. Multi-Graph Convolutional Layer
为了获得多样化的空间相关性和上下文信息,本文使用多图网络来捕获异构的空间相关性。多图网络可以聚合不同领域的数据,捕获多个空间相关性,并单独学习。例如,文献[25,26]分别从邻近性、功能相似性和连通性对空间相关性进行建模。文献[31]使用历史交通模式相关性对异质空间进行建模。然而,他们都忽视了长距离和流量之间的相关性对空间建模的影响。在本节中,我们使用多个图形对道路和这些关系之间的不同相关性进行编码。
4.2.1. Multi-Graph Construction
利用多个图对道路之间的三种相关性进行建模,包括:(1)邻接图adjacency graph,,编码空间接近度;(2) 交通连通图 traffic connectivity graph,考虑相对遥远区域之间的连通性;(3)区域相似图regional similarity graph,对动态方向相似的节点进行编码。
(1) Traffic Adjacency Graph
本文定义了基于空间邻近性的交通邻接图( X w X_w Xw),每对节点( v i , v j v_i,v_j vi,vj)之间是否有一条直线,如果 v i v_i vi和 v j v_j vj连接,则 X w , i j = 1 。否则, X_{w,ij}=1。否则, Xw,ij=1。否则,X_{w,ij}=0$。邻接图的计算如下:

图5给出了邻接矩阵的一个例子:
(2)Traffic Connectivity Graph
由于交通状态是时间序列数据,道路上的当前交通状态将不可避免地影响那些地理位置遥远但易于访问的位置。例如,当 X i j = 1 、 X j k = 1 和 X i k = 0 X_{ij}=1、X_{jk}=1和X_{ik}=0 Xij=1、Xjk=1和Xik=0时,节点 i i i和 k k k不直接连接,信息可以通过节点 j j j传输。如果发生拥塞或其他事故,非相邻节点对之间的流量传输需要绕过中间节点对来发送拥塞信息。为了保证数据是否可以传输,我们根据实际距离判断远程节点是否可以到达。如果节点可访问,则可以发送信息;这是一种远距离关联。因此,本文定义的交通连通图为:

where, v ˉ i j \bar{v}_{ij} vˉij是节点 i i i和 j j j之间的平均速度,它是指驾驶员在没有任何不利条件的情况下驾驶的平均速度, m m m是以平均速度移动的时间步数。因此, m m m决定 X p X_p Xp的元素大小。如果车辆可以在 m m m个时间步内从节点 i i i行驶到 j j j,则元素 X p , i j = 1 X_{p,ij}=1 Xp,ij=1,否则 X p , i j = 0 X_{p,ij}=0 Xp,ij=0。直观地说, X p , i j X_{p,ij} Xp,ij用于检测车辆是否可以在特定的时间步数内以平均速度从节点 i i i行驶到节点 j j j。在这里,将 X p X_p Xp的所有对角线值设置为0。
(3)Regional Similarity Graph
为了同时考虑不同节点的相似性,我们使用皮尔逊相关方法来描述它们。在以前的文献[39,40]中,皮尔逊相关法主要分析时间序列是否相关。相比之下,本文使用皮尔逊相关法来检验区域空间位置是否相关。在许多情况下,具有相似空间位置的道路在空间上不一定很近。例如,商业区和学区都有相同的交通模式。尽管如此,在工作日的高峰时段,当商业区有大量交通流量时,学区也可能很快有大量交通流量。可以看出,不同的空间区域具有相似的位置。因此,我们使用Pearson相关法构建节点间的流量关系,将其视为权重 w s ( i , j ) w_s(i,j) ws(i,j), w s ( i , j ) w_s(i,j) ws(i,j)的计算如式(8)所示:
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第7张图片](http://img.e-com-net.com/image/info8/621a805b34e941cf977a03f973595174.jpg)
where, x i τ x^τ_i xiτ和 y j τ y^τ_j yjτ分别是节点 i i i和 j j j在时间 τ τ τ的流量。 L L L是时间序列的长度。 x ˉ \bar{x} xˉ和 y ˉ \bar{y} yˉ是节点 i i i和 j j j在时间长度 L L L下的平均交通流量, w s ( i , j ) ∈ [ 0 , 1 ] w_s(i,j)∈ [0,1] ws(i,j)∈[0,1]. 然后,区域相似图 X s X_s Xs可以表示为公式(9),其中 σ = 0.5 σ=0.5 σ=0.5。
4.2.2. Multi-Graph Convolutional Network
为了捕获多样性和异质性空间相关性,我们采用了多图卷积网络(MGCN)模型,该模型由多个单独的图结构组成,并将具有不同空间位置关系的每个节点的特征输入到一个单独的图中,然后使用基于谱理论的图卷积分析时间片上的图拓扑。在图分析中,GCN层和1阶滤波器的叠加可以达到类似于k阶切比雪夫多项式滤波器的效果【41】,从而提高了训练速度和预测精度。切比雪夫多项式的分层传播定律为:

where, H ∈ R u × 1 , X ∈ R v × 1 H∈R^{u×1},X∈R^{v×1} H∈Ru×1,X∈Rv×1和 W k ∈ R v × u W_k∈R^{v×u} Wk∈Rv×u表示隐藏层、输入特征向量和操作中提取的可训练参数矩阵;ReLU是激活功能;和 L ~ ∈ R v × v \tilde{L}∈R^{v×v} L~∈Rv×v是重新缩放的拉普拉斯矩阵, L ~ = 2 λ m a x L − I N \tilde{L} =\frac{2}{λ_{max}}L−I_N L~=λmax2L−IN,其中 L = I N − D − 1 / 2 A D − 1 / 2 L=I_N−D^{−1/2}AD^{−1/2} L=IN−D−1/2AD−1/2是对称归一化拉普拉斯图, λ m a x λ_{max} λmax是其最大特征值。 I N I_N IN是单位矩阵, A A A是邻接矩阵, D D D是度矩阵。传播定律可以看作是傅里叶域中的一个谱滤波器spectral filter。每个路段输入三个GCN和由相应道路图生成的三个特征矩阵。本文定义的一阶GCN层的传播规律为:
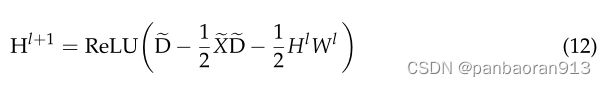
where, X ~ ∈ R v × v \tilde{X}∈R^{v×v} X~∈Rv×v是拓扑图确定的邻接矩阵, D ~ \tilde{D} D~是 X ~ \tilde{X} X~的对角度矩阵, H l H^l Hl是 L L L层的特征矩阵, W l W^l Wl是 L L L层的参数矩阵。
4.3. Cross-Attention Mechanism Fusion
虽然可以使用多个图形作为输入,但如何同时有效地集成时间和空间信息是当前研究阶段的一个新问题。在文献[42]中,时空特征通过时空融合图的矩阵乘法进行融合。文献[43]通过对生成的拓扑图进行求和和集成,直接合并了所有特征。这些方法不能同时支持多时间和多空间信息的融合。为了有效融合多层时间切片上邻接图、连通图和区域相似图之间的相关性,我们提出了一种称为交叉注意融合机制的动态融合方法。交叉注意融合的原理是使用最基本的注意机制,以交错的方式从时间和空间角度同时捕获信息。图6显示了交叉注意机制的一般模型。
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第8张图片](http://img.e-com-net.com/image/info8/cb337ec85c2f4a208d51f3bac3004c3c.jpg)
注意力机制的博文:《详解Transformer中Self-Attention以及Multi-Head Attention》
4.3.1. Cross Attention
我们采用多层时间输入( X t − τ ∈ X i n p u t X_{t−τ}∈X_{input} Xt−τ∈Xinput(方程(5))通过多图特征集 θ θ θ(方程(5))并行,得到隐藏的时空表示 H ℍ H.

这里, H t − τ θ ∈ H H^θ_{t−τ}∈H Ht−τθ∈H、,其上标 θ θ θ携带空间相关信息,下标 t − τ t-τ t−τ携带时间相关信息。为了实现时空信息的融合,我们分两步使用时空注意机制,如图7所示。
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第9张图片](http://img.e-com-net.com/image/info8/dd602bc6904b48fd9b6c7b9eef92d055.jpg)
4.3.2. Feature Fusion
在第一步中,我们划分时空表示 H t − τ θ H^θ_{t−τ} Ht−τθ分为两种表达形式:
(1)根据时间相同但空间位置不同分为 H t X w H^{X_w}_t HtXw、 H t X p H^{X_p}_t HtXp和 H t X s H^{X_s}_t HtXs;
(2) 根据相同的空间但不同的时间信息转化为 H t − r θ H^θ_{t−r} Ht−rθ、 H t − d θ H^θ_{t−d} Ht−dθ、 and H t − w θ H^θ_{t−w} Ht−wθ.
前者表示异构多图的空间特征,称为空间注意;后者代表多层次的时间特征,称为时间注意。因此,第一步的空间注意(等式(14))和时间注意(等式(15))如下所示:
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第10张图片](http://img.e-com-net.com/image/info8/427aa56b9f3a4a0db24b3430e4ad7cd5.jpg)
其中 W H 1 t W^{1t}_H WH1t、 W M 1 t W^{1t}_M WM1t、 W H 1 s W^{1s}_H WH1s和 W G 1 s W^{1s}_G WG1s表示可培训参数; b 1 t b^{1t} b1t和 b 1 s b^{1s} b1s表示偏差向量; α τ 1 t α^{1t}_τ ατ1t和 α θ 1 s α^{1s}_θ αθ1s表示归一化权重标量,即 ∑ τ T h α τ 1 t = ∑ θ N α θ 1 s = 1 ∑^{Th}_τα^{1t}_τ=∑^N_θα^{1s}_θ=1 ∑τThατ1t=∑θNαθ1s=1,其中 α τ 1 t ∈ ( 0 , 1 ) α^{1t}_τ∈(0,1) ατ1t∈(0,1)和 α θ 1 s ∈ ( 0 , 1 ) α^{1s}_θ∈(0,1) αθ1s∈(0,1). M t 公 − τ M_{t公−τ} Mt公−τ表示时间片 h t − τ h_{t−τ} ht−τ、, G θ G^θ Gθ表示图 θ θ θ的简洁向量。
第二步,如图8所示,由于第一步是在一组时间注意中,产生了一个包含时间信息的空间集 H ( T ) = { H θ ( T ) ∣ θ ∈ ( X w , X P , X s ) } \mathbb{H}^{(T)}=\{H^{(T)}_θ∣θ∈(X_w,X_P,X_s)\} H(T)={Hθ(T)∣θ∈(Xw,XP,Xs)} 。空间注意产生一个包含空间信息的时间集 H ( S ) = { H t − τ ( S ) ∣ τ ∈ T h } \mathbb{H}^{(S)}=\{H^{(S)}_{t−τ}∣τ∈T_h\} H(S)={Ht−τ(S)∣τ∈Th};然后,我们使用交叉注意对新融合的空间集 H ( S ) \mathbb{H}^{(S)} H(S)进行时间注意,并对新融合的时间集 H ( T ) \mathbb{H}^{(T)} H(T)进行空间注意,以得到一组新的方程。
这里的表示法类似于第一步中的公式表示法。交叉注意机制融合的原理是将多层时间相关性和异质空间相关性同时表示为两个视图,然后进行交叉融合。方程(14)和(16)基于空间连续性将 H ( S ) \mathbb{H}^{(S)} H(S)压缩为 H ( S T ) H^{(ST)} H(ST),方程(15)和(17)基于时间连续性将 H ( T ) \mathbb{H}^{(T)} H(T)压缩为 H ( T S ) H^{(TS)} H(TS)。最后,将两个压缩矩阵输入到一个完全连通的层中,得到最终的预测结果,即:

其中, W T S W_{TS} WTS和 W S T W_{ST} WST为可训练参数, b b b为有偏参数。
5. Experiment
5.1. Datasets Description
我们在官方网站上下载了两个加州交通数据集PeMS04和PeMS08(https://pems.dot.ca.gov/)(2021 5月23日访问)和GitHub。交通数据每30秒实时收集一次,每5分钟聚合一次【41】。在我们的实验中考虑了三种交通测量:总流量、平均速度和距离。我们使用1小时(Tp=12)作为历史时间窗口,预测未来15/30/45/60分钟的交通状况。
PeMSD4包含29条道路上的3848个探测器。我们选择了307个传感器,收集了2018年1月1日至2月28日两个月的数据。
PeMSD8包含1979个探测器,位于8条道路上。我们选择了170个传感器,收集了2016年7月1日至8月31日两个月的数据。表1总结了这两个数据集的一些关键信息数据。
Tab.1 数据集描述和统计信息。
5.2. Settings
使用Pytorch实现我们的模型。首先,将⛄️输入时间参数设置为 T r = T p × 3 T_r=T_p×3 Tr=Tp×3、 T d = T p × 1 T_d=T_p×1 Td=Tp×1和 T w = T p × 1 T_w=T_p×1 Tw=Tp×1,其中 T p = 12 T_p=12 Tp=12是预测窗口大小。我们捕获了三种类型的位置关系,因此 N = 3 N=3 N=3。在多图卷积阶段,图和时间卷积核大小分别设置为64和3。在培训过程中,我们选择了最佳batch_size=32,learn_rate=1×10−3,epoch=100。所有实验均在Windows系统(CPU:Intel(R)Core(TM)i5-5200U [email protected] Ghz)上编译和测试,使用Xshell和WinSCP连接到服务器(GTX 1080 Ti)。
5.3. Baselines
我们将CAFMGCN与以下八条基线进行比较:
-
SVR:支持向量回归使用线性支持向量机进行回归任务[6]。
-
GRU:选通递归单元网络,一种特殊的RNN【10】。
-
DCRNN:扩散卷积递归神经网络是一种数据驱动的预测框架,使用扩散递归神经网络来捕获时空依赖性【19】。
-
STGCN:时空图卷积网络是图卷积网络和卷积序列建模层的集成框架,用于建模空间和时间依赖关系[20]。
-
Graph WaveNet:一种将自适应邻接矩阵与1D扩展卷积结合成图卷积的框架[21]。
-
ASTGCN:基于注意的时空图卷积网络将时空注意机制引入模型。只有建模期的最新组成部分用于保持公平比较【28】。
-
时空同步图卷积网络(STSGCN):时空同步图卷积网络,利用局部时空子图模块独立建模局部相关性【29】。
-
STFGNN:时空融合图神经网络可以有效地并行融合不同时期的各种时空图。我们比较了该模型的融合方法【42】。
5.4. Evaluation Metric
使用三种评估:平均绝对误差(MAE)、平均基本百分比误差(MAPE)和均方根误差(RMSE)。
5.5. Experiment Results Analysis
本文将八个基线模型与我们的模型进行了比较。从图9可以看出,与其他模型相比,我们的CAFMGCN模型在MAE、MAPE和RMSE三个评估指标上取得了最好的结果。
传统的时间序列预测方法SVR和GRU只考虑时间相关性,忽略了空间相关性的重要性,预测效果不理想。
在深入学习方法的基础上,引入DCRNN、STGCN、Graph WaveNet、ASTGCN、STSGCN、STFGNN以及我们的模型CAFMGCN、图结构和图拓扑,以获取空间信息并获得更好的预测结果。
Graph WaveNet的预测效果最差,因为它只使用1D CNN,无法堆叠其时空层和扩展感受野。
DCRNN、STGCN和ASTGCN分别使用两个模块处理时间和空间相关性,忽略了时空数据的异质性,预测效果平均。
然而,STSGCN和STFGNN同时处理时间和空间相关性,具有较高的MAE、MAPE和RMSE,但忽略了时间多样性。
我们的CAFMGCN考虑了不同的时间和异质空间相关性,同时捕获时空相关性并执行多图融合。实验结果表明,CAFMGCN能够更好地捕捉道路网络的异质时空相关性,从而达到最佳的预测效果。
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第14张图片](http://img.e-com-net.com/image/info8/5048db68ccdf491488fa0aa6a5fc6fa1.jpg)
图10显示了两个数据集中未来15、30、45和60分钟的交通流预测。以GRU、STGCN和ASTGCN为基线,从图中可以看出,随着时间的增加,每个模型的预测都呈上升趋势,但我们的模型的预测误差上升得比其他三个模型慢,因为我们考虑了长距离的时间相关性,并结合了多个图的特征来减少模型的预测误差。短期内取得了有效的预测结果,对长期预测有很大帮助。
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第15张图片](http://img.e-com-net.com/image/info8/d0d5bdd2109a4777baa0fd0ba973af49.jpg)
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第16张图片](http://img.e-com-net.com/image/info8/fe07009329b343138720e8bdad8b741d.jpg)
5.6. Ablation Experiment
为了验证多图异质性和交叉注意机制,我们以PEMS04为例进行了消融研究。对于异质性,我们基于三个单图实验,即邻接图、连通图和区域相似图,使用单变量方法用一个图来减少多个图的异质性。对于交叉注意,我们使用文献[31]中提到的矩阵乘法方法来表示多图融合和GRU模型,以供实验使用。
如图11所示,单图ASTGCN-w、ASTGCN-p、ASTGCN-s和多图非注意机制的预测效果不如CAFMGCN,说明多图的有效性和交叉注意机制的融合效果更好。
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第17张图片](http://img.e-com-net.com/image/info8/a2a4d219e8754852afdd6b56bdda9dbc.jpg)
6. Conclusions and Outlook
本文提出了一种新的交通流预测模型CAFMGCN。该模型使用多图GCN处理多级时间相关性,对异构空间道路之间的非欧几里得相关性进行编码,并将MGCN与交叉注意融合,以捕获隐藏的时间和空间信息。将多图卷积模块与交叉注意机制相结合,可以同时捕获交通数据的动态时空特性。基于两个真实流量数据集的实验证明,我们的模型CAFMGCN可以获得更好的性能。
未来主要考虑以下两个问题:天气因素一直是交通流预测面临的挑战之一。环境极大地影响了旅行,需要根据特定的天气数据进行观察。此外,生活中经常会遇到重大事件,如节日、节假日和音乐会,这很容易造成交通堵塞。解决这些问题将进一步改善运输系统。
References
[16]A Deep Learning Model for Traffic Speed Prediction,LC-RNN博文
[17]Traffic graph convolutional recurrent neural network: A deep learning framework for network-scale traffic learning and forecasting.,原文
[18] Deep spatial–temporal 3D convolutional neural networks for traffic data forecasting. 知乎
[19]Diffusion convolutional recurrent neural network: Data-driven traffic forecasting,⭐️DCRNN简书
[20]Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. STGCN简书
[21]Graph wavenet for deep spatial-temporal graph modeling.,⭐️GWT博文
[22]Dynamic Spatial-Temporal Graph Convolutional Neural Networks for Traffic Forecasting,博文
[23]Multistep speed prediction on traffic networks: A deep learning approach considering Spatio-temporal dependencies,原文
[24]Composition-based multi-relational graph convolutional networks,博文
[25]Bike flow prediction with multi-graph convolutional networks.MGCN我的博文
[26]Spatiotemporal multi-graph convolution network for ride-hailing demand forecasting.⭐️ST-MGCN.我的博文
[27]TrafficGan: Network-scale deep traffic prediction with generative adversarial nets.,原文
[28]Attention based spatial-temporal graph convolutional networks for traffic flow forecasting,⭐️ASTGCN知乎
[29]Spatial-temporal synchronous graph convolutional networks: A new framework for spatial-temporal network data forecasting.,⭐️STSGCN博文
[30]Multi-graph convolutional network for short-term passenger flow forecasting in urban rail transit,原文
[31]emporal multi-graph convolutional network for traffic flow prediction,博文
[32]Neural machine translation by jointly learning to align and translate,简书
[33]Multi-range attentive bicomponent graph convolutional network for traffic forecasting.,博文
[34]A3t-gcn: Attention temporal graph convolutional network for traffic forecasting,博文
[35]Self-attention generative adversarial networks.,博文
[36]Ccnet: Criss-cross attention for semantic segmentation,博文
[37] CaEGCN: Cross-Attention Fusion based Enhanced Graph Convolutional Network for Clustering,博文
[38]Forecasting Ambulance Demand with Profiled Human Mobility via Heterogeneous Multi-Graph Neural Networks. ,原文
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第2张图片](http://img.e-com-net.com/image/info8/013e50b0bdb144218bb676027709d5c8.jpg)
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第6张图片](http://img.e-com-net.com/image/info8/3f384040bb274487bedfe70e484d14e1.jpg)
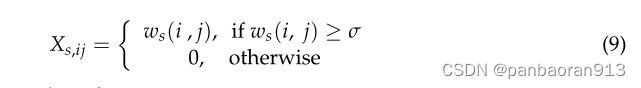

![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第11张图片](http://img.e-com-net.com/image/info8/59d221e4eda54258b7378d5dc84d8c55.jpg)
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第12张图片](http://img.e-com-net.com/image/info8/cfbba44c9f65493b8846e0afeff2aff1.jpg)
![[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for_第13张图片](http://img.e-com-net.com/image/info8/9b5d30003dd948d2a19ad60fafd93b8b.jpg)