【Ryo】Python：绘图之Matplotlib

利用Python进行图形描绘是美化图形，进行数分可视化展示的重要途径。本文缝合了许多保姆级教学的案例，整理自用欢迎大家参考~

研究内容	软件	日期
图形绘制	Python3(vs)	2021年6月5日

△△△△△本文为个人项目练习，仅供参考，如有不足欢迎讨论 △△△△△

一、神器Matplotlib

绘图的包基本上就几个，对于大部分的绘图完全够用了。matplotlib首当其冲，是最常用、最新手的绘图包，功能强大调用方便。matplotlib是受MATLAB的启发构建的。MATLAB是数据绘图领域广泛使用的语言和工具。MATLAB语言是面向过程的。利用函数的调用，MATLAB中可以轻松的利用一行命令来绘制直线，然后再用一系列的函数调整结果。

1. 首先介绍一些利用matplotlib进行绘图的基本框架：
   在绘图结构中，figure创建窗口，subplot创建子图。所有的绘画只能在子图上进行。plt表示当前子图，若没有就创建一个子图。所有你会看到一些教程中使用plt进行设置，一些教程使用子图属性进行设置。他们往往存在对应功能函数。figure只能有一个，是大的画布，而子图顾名思义有可以有很多个，是画布内的各个图形。
2. 常见配置参数：
   axex: 设置坐标轴边界和表面的颜色、坐标刻度值大小和网格的显示
   figure: 控制dpi、边界颜色、图形大小、和子区( subplot)设置
   font: 字体集（font family）、字体大小和样式设置
   grid: 设置网格颜色和线性
   legend: 设置图例和其中的文本的显示
   line: 设置线条（颜色、线型、宽度等）和标记
   patch: 是填充2D空间的图形对象，如多边形和圆。控制线宽、颜色和抗锯齿设置等。
   savefig: 可以对保存的图形进行单独设置。例如，设置渲染的文件的背景为白色。
   verbose: 设置matplotlib在执行期间信息输出，如silent、helpful、debug和debug-annoying。
   xticks和yticks: 为x,y轴的主刻度和次刻度设置颜色、大小、方向，以及标签大小。
3. 进行画布和子图布局：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator

#创建窗口、子图
#先创建窗口，再创建子图。（一定绘制）
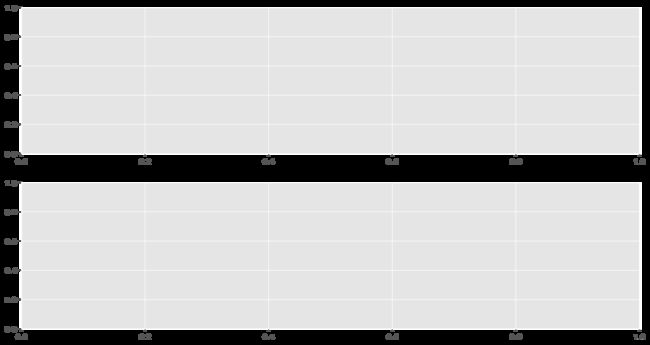
fig = plt.figure(num=1, figsize=(15, 8),dpi=200)     #开启一个窗口，同时设置大小，分辨率
ax1 = fig.add_subplot(2,1,1)  #通过fig添加子图，参数：行数，列数，第几个。
ax2 = fig.add_subplot(2,1,2)  #通过fig添加子图，参数：行数，列数，第几个。
print(fig,ax1,ax2)

这样就完成绘制了上下两个子图的一张图：（坐标轴默认参数0-1）

4. 设置子图的细节各个参数：

ax1.set_title('python-drawing')            #设置图体，plt.title
ax1.set_xlabel('x-name')                    #设置x轴名称,plt.xlabel
ax1.set_ylabel('y-name')                    #设置y轴名称,plt.ylabel
plt.axis([-6,6,-10,10])                  #设置横纵坐标轴范围，这个在子图中被分解为下面两个函数
ax1.set_xlim(-5,5)                           #设置横轴范围，会覆盖上面的横坐标,plt.xlim
ax1.set_ylim(-10,10)                         #设置纵轴范围，会覆盖上面的纵坐标,plt.ylim
xmajorLocator = MultipleLocator(2)   #定义横向主刻度标签的刻度差为2的倍数。就是隔几个刻度才显示一个标签文本
ymajorLocator = MultipleLocator(3)   #定义纵向主刻度标签的刻度差为3的倍数。就是隔几个刻度才显示一个标签文本

ax1.xaxis.set_major_locator(xmajorLocator) #x轴 应用定义的横向主刻度格式。如果不应用将采用默认刻度格式
ax1.yaxis.set_major_locator(ymajorLocator) #y轴 应用定义的纵向主刻度格式。如果不应用将采用默认刻度格式

ax1.xaxis.grid(True, which='major')      #x坐标轴的网格使用定义的主刻度格式
ax1.yaxis.grid(True, which='major')      #x坐标轴的网格使用定义的主刻度格式

ax1.set_xticks([])     #去除坐标轴刻度
ax1.set_xticks((-5,-3,-1,1,3,5))  #设置坐标轴刻度
ax1.set_xticklabels(labels=['x1','x2','x3','x4','x5'],rotation=-30,fontsize='small')  #设置刻度的显示文本，rotation旋转角度，fontsize字体大小

这样就完成在子图上分别绘制坐标参数参数：

5. 极坐标绘图

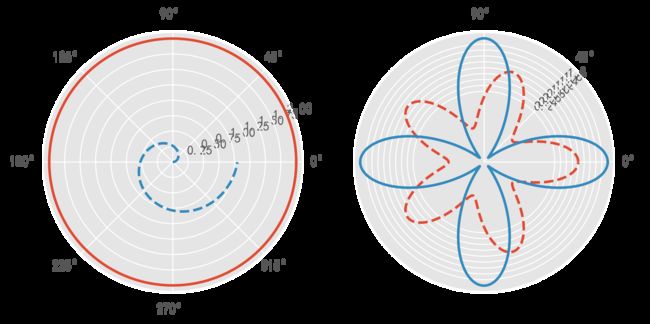
#极坐标
plt.show()
fig = plt.figure(2)                                #新开一个窗口
ax1 = fig.add_subplot(1,2,1,polar=True)                  #启动一个极坐标子图
theta=np.arange(0,2*np.pi,0.02)              #角度数列值
ax1.plot(theta,2*np.ones_like(theta),lw=2)   #画图，参数：角度，半径，lw线宽
ax1.plot(theta,theta/6,linestyle='--',lw=2)           #画图，参数：角度，半径，linestyle样式，lw线宽

ax2 = fig.add_subplot(1,2,2,polar=True)                  #启动一个极坐标子图
ax2.plot(theta,np.cos(5*theta),linestyle='--',lw=2)
ax2.plot(theta,2*np.cos(4*theta),lw=2)

ax2.set_rgrids(np.arange(0.2,2,0.2),angle=45)   #距离网格轴，轴线刻度和显示位置
ax2.set_thetagrids([0,45,90])                   #角度网格轴，范围0-360度

plt.show()

6. 柱状图

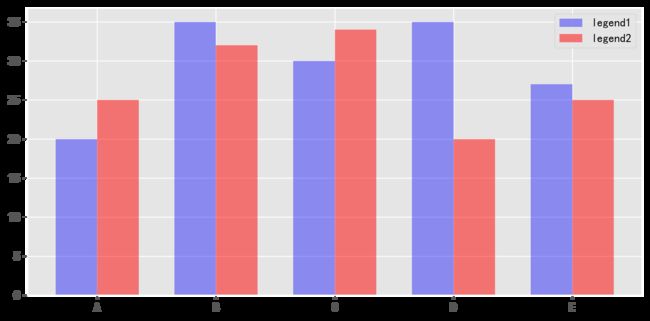
#柱状图
plt.figure(3)
x_index = np.arange(5)   #柱的索引
x_data = ('A', 'B', 'C', 'D', 'E')
y1_data = (20, 35, 30, 35, 27)
y2_data = (25, 32, 34, 20, 25)
bar_width = 0.35   #定义一个数字代表每个独立柱的宽度

rects1 = plt.bar(x_index, y1_data, width=bar_width,alpha=0.4, color='b',label='legend1')            #参数：左偏移、高度、柱宽、透明度、颜色、图例
rects2 = plt.bar(x_index + bar_width, y2_data, width=bar_width,alpha=0.5,color='r',label='legend2') #参数：左偏移、高度、柱宽、透明度、颜色、图例
#关于左偏移，不用关心每根柱的中心不中心，因为只要把刻度线设置在柱的中间就可以了
plt.xticks(x_index + bar_width/2, x_data)   #x轴刻度线
plt.legend()    #显示图例
plt.tight_layout()  #自动控制图像外部边缘，此方法不能够很好的控制图像间的间隔
plt.show()

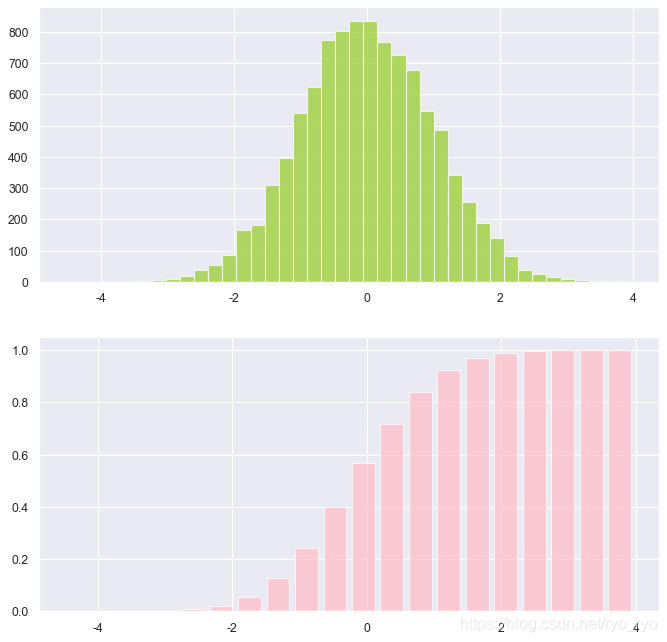
7. 直方图（Py2中density为normed，目前Py3中该参数已变成density）

#直方图
fig,(ax0,ax1) = plt.subplots(nrows=2,figsize=(10,10),dpi=80)     #在窗口上添加2个子图
sigma = 1   #标准差
mean = 0    #均值
x=mean+sigma*np.random.randn(10000)   #正态分布随机数
ax0.hist(x,bins=40,density=False,histtype='bar',facecolor='yellowgreen',alpha=0.75)   #density是否归一化，histtype直方图类型，facecolor颜色，alpha透明度
ax1.hist(x,bins=20,density=1,histtype='bar',facecolor='pink',alpha=0.75,cumulative=True,rwidth=0.8) #bins柱子的个数,cumulative是否计算累加分布，rwidth柱子宽度
plt.show()  #所有窗口运行

结果如下所示：

8. 热力图

#直方图
fig,(ax0,ax1) = plt.subplots(nrows=2,figsize=(10,10),dpi=80)     #在窗口上添加2个子图
sigma = 1   #标准差
mean = 0    #均值
x=mean+sigma*np.random.randn(10000)   #正态分布随机数
ax0.hist(x,bins=40,density=False,histtype='bar',facecolor='yellowgreen',alpha=0.75)   #density是否归一化，histtype直方图类型，facecolor颜色，alpha透明度
ax1.hist(x,bins=20,density=1,histtype='bar',facecolor='pink',alpha=0.75,cumulative=True,rwidth=0.8) #bins柱子的个数,cumulative是否计算累加分布，rwidth柱子宽度
plt.show()  #所有窗口运行

结果如下所示：

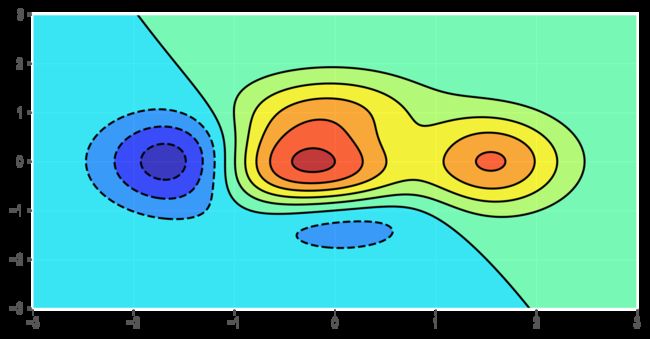
9. 三维表面图

#-*- coding:utf-8 -*-
from pylab import *

def f(x,y): return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)

n = 256
x = np.linspace(-3,3,n)
y = np.linspace(-3,3,n)
X,Y = np.meshgrid(x,y)

contourf(X, Y, f(X,Y), 8, alpha=.75, cmap='jet')
C = contour(X, Y, f(X,Y), 8, colors='black', linewidth=.5)
show()

结果如下所示：

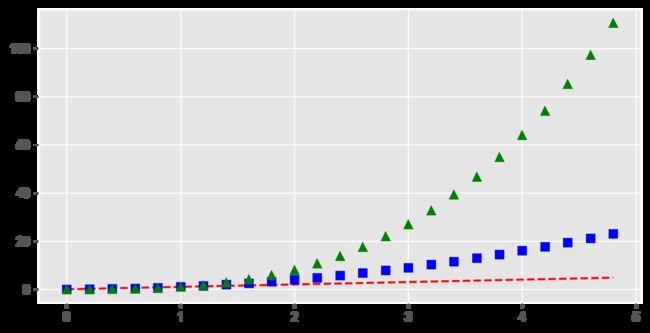
10. 叠加图

#叠加线
import numpy as np
import matplotlib.pyplot as plt

# evenly sampled time at 200ms intervals
t = np.arange(0., 5., 0.2)

# red dashes, blue squares and green triangles
plt.plot(t, t, 'r--', t, t**2, 'bs', t, t**3, 'g^')
plt.show()

结果如下所示：

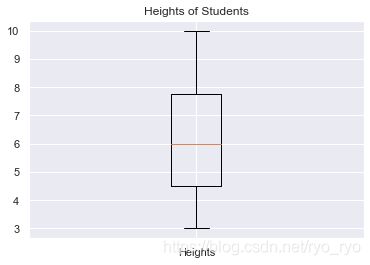
11. 箱线图

#绘制箱型图
def drawBox(heights):
    #创建箱型图
    #第一个参数为待绘制的定量数据
    #第二个参数为数据的文字说明
    pyplot.boxplot([10,3,5,7],labels=['Heights'])
    pyplot.title('Heights of Students')
    pyplot.show()
drawBox(heights)

结果如下所示：

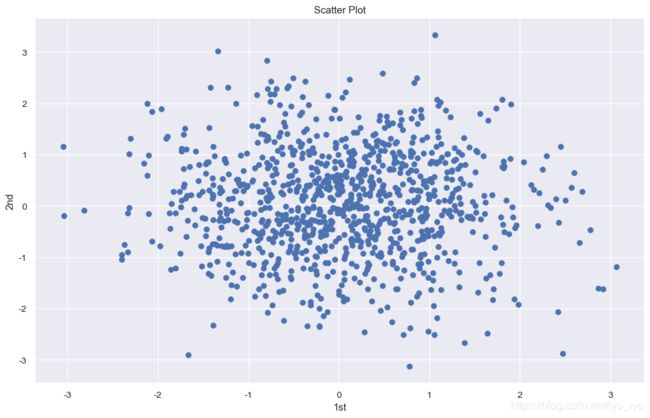
12. 散点图

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

np.random.seed(2000)
y = np.random.standard_normal((1000, 2))
plt.figure(figsize=(13,8),dpi=90)
plt.scatter(y[:,0],y[:,1],marker='o')
plt.grid(True)
plt.xlabel('1st')
plt.ylabel('2nd')
plt.title('Scatter Plot')
plt.show()

结果如下所示：

二、运用参数

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.figure()    # 创建画布
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置字体，不然中文无法显示

plt.rcParams['figure.figsize'] = (8.0, 4.0) # 设置figure_size尺寸
#figsize(12.5, 4) # 设置 figsize
plt.rcParams['savefig.dpi'] = 300 #保存图片分辨率
plt.rcParams['figure.dpi'] = 300 #分辨率
# 默认的像素：[6.0,4.0]，分辨率为100，图片尺寸为 600&400
# 指定dpi=200，图片尺寸为 1200*800
# 指定dpi=300，图片尺寸为 1800*1200

plt.rcParams['image.interpolation'] = 'nearest' # 设置 interpolation style
plt.rcParams['image.cmap'] = 'gray' # 设置 颜色 style

画一个电视机雪花界面的饼图！

plt.pie(x, explode=None, labels=None,
    colors=('b', 'g', 'r', 'c', 'm', 'y', 'k', 'w'),
    autopct=None, pctdistance=0.6, shadow=False,
    labeldistance=1.1, startangle=None, radius=None,
    counterclock=True, wedgeprops=None, textprops=None,
    center = (0, 0), frame = False )
plt.show()

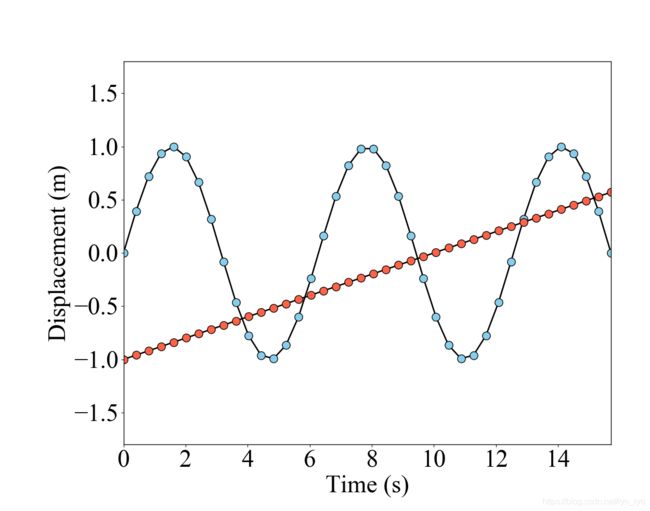
二、简单绘图1——sinx和直线

下面以sinx和直线为例，对于一张图片有以下组成

1. 坐标轴X、Y，其范围和间距刻度
2. 图片四条边框（线条）
3. 图片刻度字体、标题字体
4. 绘制图形的函数
5. 图形的点、线的形态（大小、粗细、颜色）

from matplotlib import pyplot as plt
import numpy as np

x = np.linspace(0, 5*np.pi, 40)
y1 = np.sin(x)
y2 = 0.1*x-1

plt.figure(figsize=(12.5, 10))
# 线条颜色black, 线宽2, 标记大小11, 标记填充颜色从网上找16进制好看的颜色
plt.plot(x, y1, '-o', color='black', markersize=11, markerfacecolor='#87CEEB', linewidth=2)
plt.plot(x, y2, '-o', color='black', markersize=11, markerfacecolor='#FF6347', linewidth=2)

# 字体设置: 字体名称Times New Roman, 字体大小34
font_format = {'family':'Times New Roman', 'size':34}
plt.xlabel('Time (s)', font_format)
plt.ylabel('Displacement (m)', font_format)
# 设置坐标轴 x范围0~5pi, y范围-1.8~1.8
plt.axis([0, 5*np.pi, -1.8, 1.8])
# 横纵坐标上的字体大小与类型(不是xlabel, 是xticks)
plt.xticks(fontproperties='Times New Roman', size=34)
plt.yticks(fontproperties='Times New Roman', size=34)
# 整个图像与展示框的相对位置
plt.subplots_adjust(left=0.19,right=0.94, bottom=0.13)
# 调整上下左右四个边框的线宽为1
ax=plt.gca()
ax.spines['bottom'].set_linewidth(1)
ax.spines['left'].set_linewidth(1)
ax.spines['right'].set_linewidth(1)
ax.spines['top'].set_linewidth(1)
plt.show()

结果如下图所示：

三、简单绘图2——常用的统计图

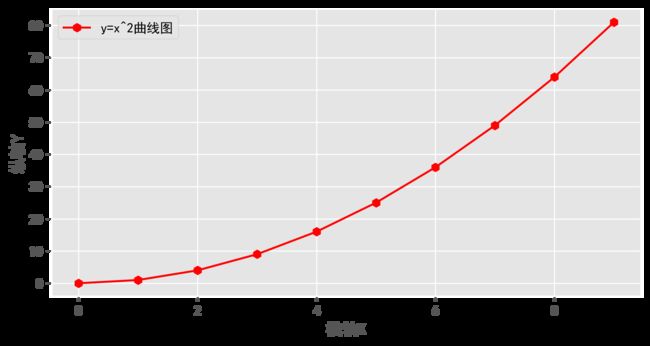
1.绘制y=x²的图像

import matplotlib.pyplot as plt
import pylab as pl
x = range(10)  # 横轴的数据
y = [i*i for i in x]  # 纵轴的数据
pl.plot(x, y, 'hr-', label=u'y=x^2曲线图')  # 显示数据点+线（有颜色）,再加上label参数添加图例
pl.legend()  # 让图例生效
pl.xlabel(u"横轴X")
pl.ylabel(u"纵轴Y")

结果如下图：

四、三线绘制

简单绘制

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt  # 导入图形展示库
plt.figure(figsize=(10,5)) #创建画布
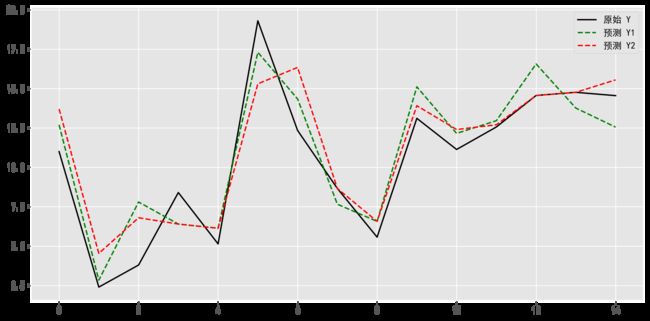
y_test = [11,2.4,3.8,8.4,5.14,19.3,12.34,8.66,5.57,13.11,11.134,12.56,14.56,14.76,14.55]
pre_y = [12.7,2.84,7.8,6.4,6.14,17.3,14.34,7.66,6.57,15.11,12.154,12.96,16.56,13.76,12.55]
pre_y2 = [13.7,4.54,6.8,6.4,6.13,15.3,16.34,8.66,6.57,13.91,12.4,12.7,14.56,14.76,15.55]
plt.plot(np.arange(len(y_test)),y_test, color='k', label='原始 Y')       #画出原始值的曲线
plt.plot(np.arange(len(pre_y)), pre_y, 'g--', label='预测 Y1')      #画出预测结果线1
plt.plot(np.arange(len(pre_y2)), pre_y2, 'r--', label='预测 Y2')      #画出预测结果线2
plt.legend(loc='upper right')                                            #图例位置
plt.tight_layout()                                                       #自动调整子图间隔

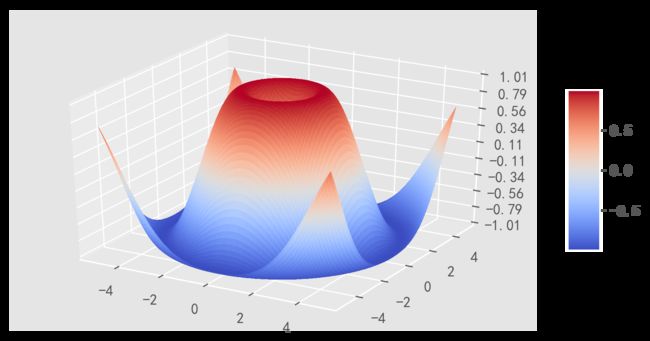
五、三维绘图

三维曲面简单绘制：

fig = plt.figure(dpi=100,figsize=(12,10))  #定义新的三维坐标轴，定义画布大小和分辨率
ax3 = plt.axes(projection='3d')

#定义三维数据
xx = np.arange(-6,6,0.2)
yy = np.arange(-6,6,0.2)
X, Y = np.meshgrid(xx, yy)
Z = np.sin(X)+np.cos(Y)

#作图
ax3.plot_surface(X,Y,Z,rstride = 1, cstride = 1,cmap='rainbow') #其中的row和cloum_stride为横竖方向的绘图采样步长，越小绘图越精细。
#ax3.contour(X,Y,Z, zdim='z',offset=-2，cmap='rainbow)   #等高线图，要设置offset，为Z的最小值
plt.show()

等高线，同时还可以将等高线投影到不同的面上：

from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

#定义坐标轴
fig4 = plt.figure(dpi=120,figsize=(10,8))
ax4 = plt.axes(projection='3d')

#生成三维数据
xx = np.arange(-5,5,0.1)
yy = np.arange(-5,5,0.1)
X, Y = np.meshgrid(xx, yy)
Z = np.sin(np.sqrt(X**2+Y**2))

#作图
ax4.plot_surface(X,Y,Z,alpha=0.3,cmap='winter')     #生成表面， alpha 用于控制透明度
ax4.contour(X,Y,Z,zdir='z', offset=-3,cmap="rainbow")  #生成z方向投影，投到x-y平面
ax4.contour(X,Y,Z,zdir='x', offset=-6,cmap="rainbow")  #生成x方向投影，投到y-z平面
ax4.contour(X,Y,Z,zdir='y', offset=6,cmap="rainbow")   #生成y方向投影，投到x-z平面
#ax4.contourf(X,Y,Z,zdir='y', offset=6,cmap="rainbow")   #生成y方向投影填充，投到x-z平面，contourf()函数

#设定显示范围
ax4.set_xlabel('X')
ax4.set_xlim(-6, 4)  #拉开坐标轴范围显示投影
ax4.set_ylabel('Y')
ax4.set_ylim(-4, 6)
ax4.set_zlabel('Z')
ax4.set_zlim(-3, 3)

plt.show()

随机散点图：

#函数定义
matplotlib.pyplot.scatter(x, y, 
	s=None,   #散点的大小 array  scalar
	c=None,   #颜色序列   array、sequency
	marker=None,   #点的样式
	cmap=None,    #colormap 颜色样式
	norm=None,    #归一化  归一化的颜色camp
	vmin=None, vmax=None,    #对应上面的归一化范围
 	alpha=None,     #透明度
	linewidths=None,   #线宽
	verts=None,   #
	edgecolors=None,  #边缘颜色
	data=None,              #本来这里还有一行	**kwargs ，但是加入这个动态变量会说还未定义报错，因此删除
	)

#ref:https://matplotlib.org/api/_as_gen/matplotlib.pyplot.scatter.html

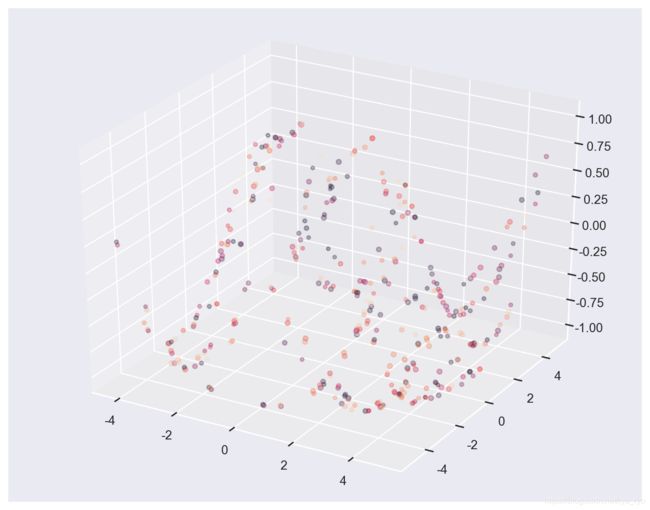
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

#定义坐标轴
fig4 = plt.figure(dpi=160,figsize=(10,8))
ax4 = plt.axes(projection='3d')

#生成三维数据
xx = np.random.random(20)*10-5   #取100个随机数，范围在5~5之间
yy = np.random.random(20)*10-5
X, Y = np.meshgrid(xx, yy)
Z = np.sin(np.sqrt(X**2+Y**2))

#作图
ax4.scatter(X,Y,Z,alpha=0.3,c=np.random.random(400),s=np.random.randint(10,20, size=(20, 40)))     #生成散点.利用c控制颜色序列,s控制大小

#设定显示范围

plt.show()

参考文献

知乎1
知乎2
简书1
CSDN1

附录——图形参数

颜色（color 简写为 c）：
蓝色： 'b' (blue)
绿色： 'g' (green)
红色： 'r' (red)
蓝绿色(墨绿色)： 'c' (cyan)
红紫色(洋红)： 'm' (magenta)
黄色： 'y' (yellow)
黑色： 'k' (black)
白色： 'w' (white)

线型（linestyle 简写为 ls）：
实线： '-'
虚线： '--'
虚点线： '-.'
点线： ':'
点： '.' 

点型（标记marker）：
像素： ','
圆形： 'o'
上三角： '^'
下三角： 'v'
左三角： '<'
右三角： '>'
方形： 's'
加号： '+' 
叉形： 'x'
棱形： 'D'
细棱形： 'd'
三脚架朝下： '1'（像'丫'）
三脚架朝上： '2'
三脚架朝左： '3'
三脚架朝右： '4'
六角形： 'h'
旋转六角形： 'H'
五角形： 'p'
垂直线： '|'
水平线： '_'