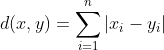机器学习算法（一） K-Means算法简述以及在MNIST上的聚类实现

目录

前言

简述

优点

缺点

距离

欧几里得距离

余弦距离

曼哈顿距离

实例：k-means在MNIST数据集的训练集上聚类（自定义）

总结

---

前言

本文面向机器学习完全从零开始，但对python有足够了解的小白（毕竟我也是），如果有人发现错误也请指正，笔者会十分感谢。已有基本了解的人可以直接跳到后文MNIST聚类实现。

环境：python 3。

调用库：numpy、struct（用来解析数据，暂时不必了解）。

简述

 K-means算法，意为K-均值。这里的K为常数，需事先设定，简单地说，该算法就是把n个样本分成k个类别。在对样本进行分类的过程一般是以样本之间的距离作为指标。距离这个概念我们下面会讲。

伪代码如下：

function K-Means(输入数据，中心点个数K)
    获取输入数据的维度Dim和个数N
    随机生成K个Dim维的点
    while(算法未收敛)
        对N个点：计算每个点属于哪一类。
        对于K个中心点：
            1，找出所有属于自己这一类的所有数据点
            2，把自己的坐标修改为这些数据点的中心点坐标
    end
    输出结果：
end

算法收敛条件：聚类结果稳定、达到最大迭代次数等

网上有这样一个牧师布道模型来辅助理解：

有四个牧师去郊区布道，一开始牧师们随意选了几个布道点，并且把这几个布道点的情况公告给了郊区所有的居民，于是每个居民到离自己家最近的布道点去听课。
听课之后，大家觉得距离太远了，于是每个牧师统计了一下自己的课上所有的居民的地址，搬到了所有地址的中心地带，并且在海报上更新了自己的布道点的位置。
牧师每一次移动不可能离所有人都更近，有的人发现A牧师移动以后自己还不如去B牧师处听课更近，于是每个居民又去了离自己最近的布道点……
就这样，牧师每个礼拜更新自己的位置，居民根据自己的情况选择布道点，最终稳定了下来。

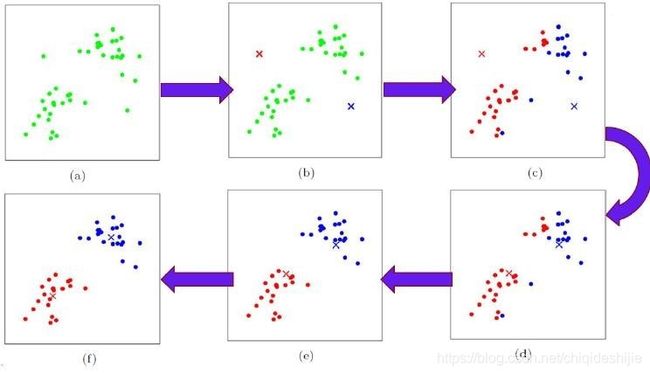
 以二维空间、欧式距离划分为例，我们再来看看这个图片加深理解：

a.一堆数据点

b.在数据点中初始化了两个中心点

c.根据离中心点的距离将数据分为两类

d.将同类数据的中心（坐标求平均值）设置为新的中心点

e.根据新的中心点，重新划分数据

f.根据新的划分结果重新寻找中心点

优点

• 容易理解；

• 算法复杂度低。

缺点

• K 值需要人为设定；

• 对K值敏感，不同 K 值得到的结果不一样；

• 对初始的中心点敏感，不同选取方式会得到不同结果；

• 对异常值敏感，比如1，3，4，5，100这一组数据质心在22.6，偏的非常离谱；

• 对数据分布敏感，不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类等等。

距离

距离是什么概念？可以简单理解为样本在某种规则下的相似程度。

本篇采用欧几里得距离。

以下为几种常用距离。

欧几里得距离

即我们所熟悉的坐标系里的两点距离。

余弦距离

即两个向量间的夹角的余弦值。

曼哈顿距离

两点的各轴间距的绝对值的总和。（这个可能会相对陌生一些，可以百度一下补补课，笔者就不干数学老师的活儿了）

实例：k-means在MNIST数据集的训练集上聚类（自定义）

我们用这样的例子来理解一下k-means、距离等具体是什么东西。

首先要知道MNIST是什么，这个详情大家自行百度，总之是一个手写体数据集，每个样本都是一个28*28的灰度图形。

下面的解码过程暂时不用深究（这里也讲不完），你只需要知道，最终解析出来的train_images和test_images是三维数组（其中一维是图片总数，train_images是60000，test_images是10000；另外两维度是28，28。没错就是灰度图形的特征）；train_labels和test_labels是一维数组（分别存放前面两个数组对应序号图片的标签）。

特征维度上的欧式距离能度量两张图片的相似程度。

import numpy as np
import struct

# 训练集文件，右边是文件地址
train_images_idx3_ubyte_file = 'MNIST_data/train-images.idx3-ubyte'
# 训练集标签文件
train_labels_idx1_ubyte_file = 'MNIST_data/train-labels.idx1-ubyte'

# 测试集文件
test_images_idx3_ubyte_file = 'MNIST_data/t10k-images.idx3-ubyte'
# 测试集标签文件
test_labels_idx1_ubyte_file = 'MNIST_data/t10k-labels.idx1-ubyte'

def decode_idx3_ubyte(idx3_ubyte_file):
    """
    解析idx3文件的通用函数
    :param idx3_ubyte_file: idx3文件路径
    :return: 数据集
    """
    # 读取二进制数据
    bin_data = open(idx3_ubyte_file, 'rb').read()

    # 解析文件头信息，依次为魔数、图片数量、每张图片高、每张图片宽
    offset = 0
    fmt_header = '>iiii' #因为数据结构中前4行的数据类型都是32位整型，所以采用i格式，但我们需要读取前4行数据，所以需要4个i。我们后面会看到标签集中，只使用2个ii。
    magic_number, num_images, num_rows, num_cols = struct.unpack_from(fmt_header, bin_data, offset)
    print('魔数:%d, 图片数量: %d张, 图片大小: %d*%d' % (magic_number, num_images, num_rows, num_cols))

    # 解析数据集
    image_size = num_rows * num_cols
    offset += struct.calcsize(fmt_header)  #获得数据在缓存中的指针位置，从前面介绍的数据结构可以看出，读取了前4行之后，指针位置（即偏移位置offset）指向0016。
    print(offset)
    fmt_image = '>' + str(image_size) + 'B'  #图像数据像素值的类型为unsigned char型，对应的format格式为B。这里还有加上图像大小784，是为了读取784个B格式数据，如果没有则只会读取一个值（即一副图像中的一个像素值）
    print(fmt_image,offset,struct.calcsize(fmt_image))
    images = np.empty((num_images, num_rows, num_cols))
    for i in range(num_images):
        if (i + 1) % 10000 == 0:
            print('已解析 %d' % (i + 1) + '张')
            print(offset)
        images[i] = np.array(struct.unpack_from(fmt_image, bin_data, offset)).reshape((num_rows, num_cols))
        offset += struct.calcsize(fmt_image)


    return images #这是num_row*num_col的ndarray


def decode_idx1_ubyte(idx1_ubyte_file):
    """
    解析idx1文件的通用函数
    :param idx1_ubyte_file: idx1文件路径
    :return: 数据集
    """
    # 读取二进制数据
    bin_data = open(idx1_ubyte_file, 'rb').read()

    # 解析文件头信息，依次为魔数和标签数
    offset = 0
    fmt_header = '>ii'
    magic_number, num_images = struct.unpack_from(fmt_header, bin_data, offset)
    print('魔数:%d, 图片数量: %d张' % (magic_number, num_images))

    # 解析数据集
    offset += struct.calcsize(fmt_header)
    fmt_image = '>B'
    labels = np.empty(num_images)
    for i in range(num_images):
        if (i + 1) % 10000 == 0:
            print ('已解析 %d' % (i + 1) + '张')
        labels[i] = struct.unpack_from(fmt_image, bin_data, offset)[0]
        offset += struct.calcsize(fmt_image)
    return labels

方便起见我们定义4个函数分别去解码对应文件。上一代码块和这一代码块写在同一个py文件里，命名为loader.py。

def load_train_images(idx_ubyte_file=train_images_idx3_ubyte_file):
    return decode_idx3_ubyte(idx_ubyte_file)


def load_train_labels(idx_ubyte_file=train_labels_idx1_ubyte_file):
    return decode_idx1_ubyte(idx_ubyte_file)


def load_test_images(idx_ubyte_file=test_images_idx3_ubyte_file):
    return decode_idx3_ubyte(idx_ubyte_file)


def load_test_labels(idx_ubyte_file=test_labels_idx1_ubyte_file):
    return decode_idx1_ubyte(idx_ubyte_file)

接下来我们定义kmeans类。

这个定义过程是自己写的，与sklearn中的定义可能不太相同，也因此可能会有代码冗余等，如有人愿意帮忙修改，感激不尽。

import numpy as np
import loader
class Kmeans:
    def __init__(self,k,maxiter,data,labels):
        self.k = k  #k是簇的数目
        self.maxiter=maxiter  #最大迭代次数
        self.data=data  
        #输入的数据，是一个(m,n*n)的数组，m代表有m个测试图，n*n是特征。
        #（例如由图片28*28二维矩阵转化为这个784一维矩阵）
        self.labels=labels  #标签文件，也是一个对应位置的一维矩阵。
        self.distances=np.zeros((self.data.shape[0],self.k))
        #data.shape[0]代表测试图数目（前文注释的m）。
        #data.shape[1]代表测试图特征（前文注释的n*n）。
        #创建个空的(m,k)数组，用来保存距离。
        self.centre=np.zeros((self.k,self.data.shape[1]))
        #创建个空的(k,n*n)数组，用来保存中心点。
        
    def get_distances(self):  
        #计算每幅图到每个中心图距离的函数，算得的距离保存为一个(m,k)数组。
        #这个数组在m上的索引顺序与data相同，即还是按照原来的顺序对应图片。
        for i in range(self.data.shape[0]):  #对每幅图进行计算。
            distance_i=((np.tile(self.data[i],(self.k,1))-self.centre)**2).sum(axis=1) ** 0.5
            #计算每个点到中心点的距离，得到一个长度k的一维数组。
            self.distances[i]=distance_i  
            #将得到的一维数组放在distances的对应位置，k轴从0到k-1。
            
    def get_centre(self): #初始化中心点，并初始化分类数组。
        self.classifications=np.random.randint(0,self.k,(self.data.shape[0]))
        #创建一个(m,)的分类数组，里面填充[0,k)的随机整数，代表每个图的初始化聚类。
        for i in range(self.k):
            self.classifications[i]=i
            #防止出现空的聚类使后面中心点计算报错。
    
    
    def classify(self):  #分类的函数。
        new_classifications=np.argmin(self.distances,axis=1)
        #计算【距离数组里每一行的最小值的索引】所组成的一维数组。
        if any(self.classifications-new_classifications):
            self.classifications=new_classifications
            #如果得到的一维数组与之前的分类数组不完全相同，则该数组作为新分类数组。
            return 1
            #返回值控制外部循环。
        else:
            return 0
        #如果完全相同就跳过，不用再替换了。返回值控制外部循环。
        
    def update_centre(self):  #更新中心点的函数。
        for i in range(self.k):
            self.centre[i] = np.mean(self.data[self.classifications==i], axis=0 )
            #每个聚类的中心点是【所有标签为该聚类的点的中心】，即数据轴的平均值。
    def work(self):  #kmeans的计算函数。
        self.get_centre() #先初始化中心点。
        for i in range(self.maxiter):  #控制次数。
            self.update_centre()  #更新中心点。
            self.get_distances()  #求距离。
            if(not self.classify()):  #根据距离分类。
                break
            #如果分类不变化则停止for循环。

接下来就要开始聚类了。首先是对于数据的处理。这里我们把三维数组拉成了二维数组，代表图片数目的维度不变，代表特征的28*28二维压缩成784大小的一维。

train_images = loader.load_train_images()
train_labels = loader.load_train_labels()
test_images = loader.load_test_images()
test_labels = loader.load_test_labels()

m = 1500  # 创建一个读入数据的数组，部分选取图片进行训练。m为选取数目。
n_clusters=30 #聚类的数目，即k值
trainingMat = np.zeros((m, 784))  
#初始化存放部分选取图片的数组并拉直，即(m,n*n)的数组。置为0。
part_train_labels=train_labels[0:m]  #直接截取出存放这部分图片标签的数组。
for i in range(m):
    for j in range(28):
        for k in range(28):
            trainingMat[i, 28*j+k] = train_images[i][j][k]
#将前面m张图片赋给存放部分图片的数组。

运行一下我们写的kmeans。

a=Kmeans(n_clusters,300,trainingMat,part_train_labels)
a.work()

接下来检查一下预测结果。

label_num = np.zeros((n_clusters, 10))
for i in range(a.classifications.shape[0]):
    pred = int(a.classifications[i])
    truth = int(part_train_labels[i])
    label_num[pred][truth] += 1
## 查看KNN label---> number label的对应关系
label2num = label_num.argmax(axis=1)       
set( label2num ) ## 看下分类是否覆盖10个数字
train_preds = np.zeros(part_train_labels.shape)
for i in range(train_preds.shape[0]):
    train_preds[i] = label2num[a.classifications[i]]
    
print("训练数据上的精度：{}".format(np.sum(train_preds==part_train_labels) / part_train_labels.shape[0]))

以下是运行结果，大功告成。

魔数:2051, 图片数量: 60000张, 图片大小: 28*28
16
>784B 16 784
已解析 10000张
7839232
已解析 20000张
15679232
已解析 30000张
23519232
已解析 40000张
31359232
已解析 50000张
39199232
已解析 60000张
47039232
魔数:2049, 图片数量: 60000张
已解析 10000张
已解析 20000张
已解析 30000张
已解析 40000张
已解析 50000张
已解析 60000张
魔数:2051, 图片数量: 10000张, 图片大小: 28*28
16
>784B 16 784
已解析 10000张
7839232
魔数:2049, 图片数量: 10000张
已解析 10000张
训练数据上的精度：0.7466666666666667

总结

k-means算法还有很多缺陷，也因此有k-means++等众多优化方案，在此不赘述。（没力气讲了）

如果有人看的话可能还会继续更新其他的机器学习算法以及k-means后续优化。

有问题欢迎评论或私信。