基于S函数的BP神经网络PID控制器及simulink仿真

基于S函数的BP神经网络PID控制器及simulink仿真

文章来源和摘要

S函数的编写格式和运行步骤

S函数相当于simulink中自定义的软件包，当simulink中没有现成的功能模块可用时，就可以通过编写s函数的方式来进行仿真。
S函数的编写格式为

各个变量对应的含义分别为

运行步骤：

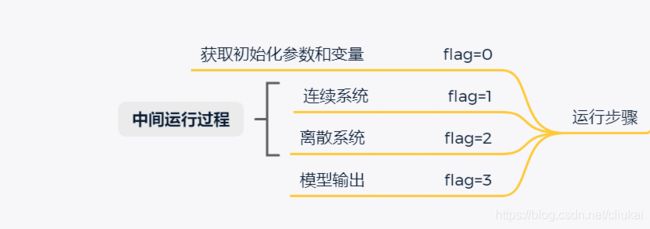
simulink模型结构

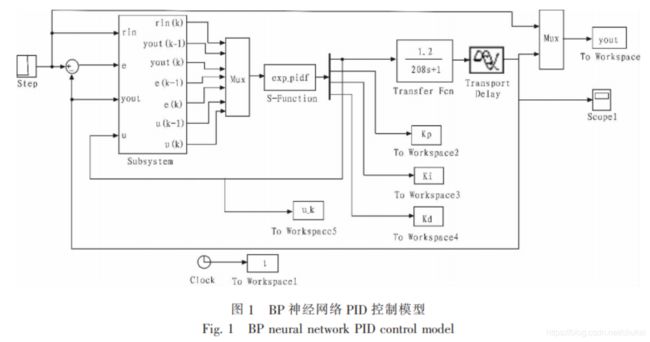
在simulink中搭建模型如下

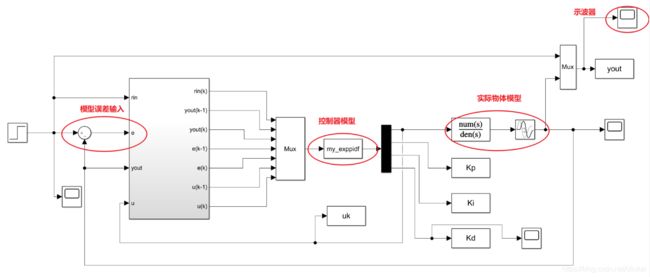
其中mux的作用是把常量合并成数组
demux（黑色部分）的作用是吧一个数组重新解析成标量
在这里有一个疑惑，就是输入的子系统中，并没有设置有效的单位延时

在BP神经网络+PID控制simulink仿真 - zkzfengyi的博客 - CSDN博客
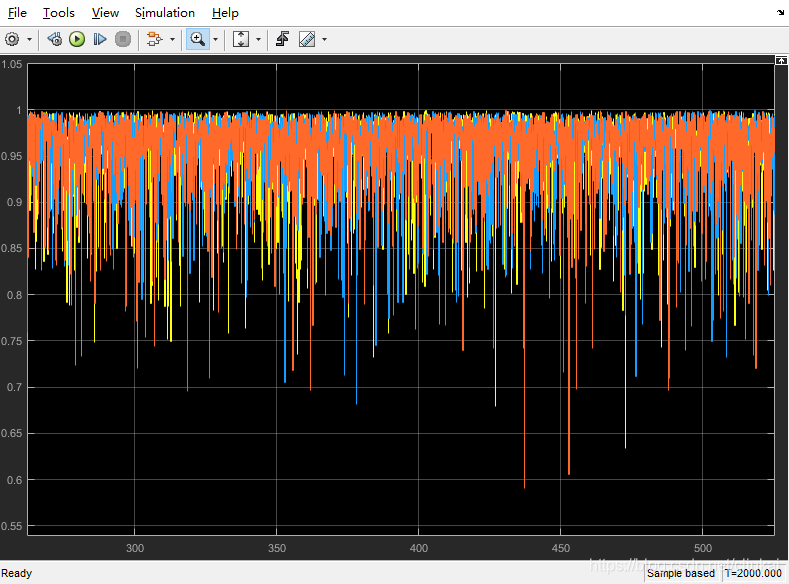
这篇博客的评论区里，大家普遍认为有造假的嫌疑，我也十分困惑。

控制器部分，利用S函数实现BP神经网络的PID。论文给出的仿真效果如下

实际的控制器仿真效果如图

PID的输出参数变化

S函数模型初始化部分代码理解

S函数总共分为4个部分，第一部分为切换函数，第二部分为初始化，第三部分为数据更新部分，第四部分为模型输出。

% 模型初始化
function[sys,x0,str,ts]=mdlInitializeSizes
    sizes=simsizes;%用于设置模块参数的结构体用simsizes来生成
    sizes.NumContStates=0;%模块连续状态变量的个数
    sizes.NumDiscStates=3;%模块离散状态变量的个数
    sizes.NumOutputs=4;%模块输出变量的个数
    sizes.NumInputs=7;%模块输入变量的个数
    sizes.DirFeedthrough=1;%模块是否存在直接贯通，1表示存在直接贯通，若为0，则mdlOutputs函数里不能有u
    sizes.NumSampleTimes=1;%模块的采样时间个数,至少是一个
    sys=simsizes(sizes);%设置完后赋给sys输出
    x0=zeros(3,1);%系统状态变量设置，3行一列
    str=[];
    ts=[0 0];%采样周期设为0表示是连续系统，
%     ts=[0.001 0];%采样周期设为0表示是连续系统，

simsizes是什么，帮助文档给出如下

ans =

包含以下字段的 struct:

NumContStates: 0
NumDiscStates: 0
 NumOutputs: 0
  NumInputs: 0
DirFeedthrough: 0
NumSampleTimes: 0

说明是一个系统的默认变量，不需要初始化就能直接引用。

S函数模型更新部分

% 模型更新部分，输入为系统状态量和系统输入
function sys=mdlUpdates(x,u)
        T=0.001;
        x=[u(5);x(2)+u(5)*T;(u(5)-u(4))/T];%3个状态量（偏差、偏差和以及偏差变化量），u(5)是偏差，u(4)是上一次的偏差，x(2)则是之前的偏差和
        sys=[x(1);x(2);x(3)];

x和u分别是什么？

u应该就是mux左侧的那7个输入变量，实际对应u(1)~u(7)

在这之前，初始化的时候，x0=zero(3,1)=[0;0;0]，这里的x正式成为状态量，分别为偏差，偏差和，偏差变化量。

所以模型更新部分实际只更新了状态量。

S函数模型输出部分

参数的初始化

% 这一段基本上都是一些参数的初始化
xite=0.2;   % 学习速率
alfa=0.05;  % 惯性因子
IN=3;H=5;OUT=3; % 神经网络的3-5-3架构

% 输入层-隐含层的加权系数
wi=rand(5,3);%产生一个5*3的随机数矩阵，随机数在（0，1）区间
wi_1=wi;wi_2=wi;wi_3=wi;    % 隐含层加权系数
% 隐含层-输出层的加权系数
wo=rand(3,5);   
wo_1=wo;wo_2=wo;wo_3=wo;    % 输出层加权系数
Oh=zeros(5,1);  %产生一个1*5的零矩阵(行矩阵)，这里就是隐含层
I=Oh;
% 输入层的具体输入
xi=[u(1),u(3),u(5)];%神经网络训练的3个输入，期望值、误差以及实际值
% PID的3个对应参量
epid=[x(1);x(2);x(3)];%3个状态变量（偏差、偏差和、偏差变化量）（3*1矩阵，列向量）
I=xi*wi';%隐层的输入

接着进行隐含层节点和输出层节点值的更新

% 更新隐含层
for j=1:1:5
% 隐含层的节点值
Oh(j)=(exp(I(j))-exp(-I(j)))/(exp(I(j))+exp(-I(j)));%隐层的输出值（1*5矩阵）行矩阵
end
% 更新输出层
K1=wo*Oh;   % 输出层的输入值（3*1矩阵）
for i=1:1:3
% 输出层的输出值
K(i)=exp(K1(i))/(exp(K1(i))+exp(-K1(i)));%得到输出层的输出（KP、KI、KD）（1*3矩阵，行向量）
end
% 这里得到的K相当于是pid的3个参数

% 最终控制器的完全输出值
u_k=K*epid;%计算得到控制律u，1个值

最后，根据反向传播算法进行权值的调整

 %隐含层至输出层的权值调整
 dyu=sign((u(3)-u(2))/(u(7)-u(6)+0.0001));
 for j=1:1:3
 dK(j)=2/(exp(K1(j))+exp(-K1(j)))^2; %输出层的输出的一阶导
 end
 for i=1:1:3
 delta3(i)=u(5)*dyu*epid(i)*dK(i);  %输出层的delta
 end
 for j=1:1:3
 for i=1:1:5
 d_wo=xite*delta3(j)*Oh(i)+alfa*(wo_1-wo_2);
 end
 end
 % 隐含层-输出层的加权系数的调整
 wo=wo_1+d_wo;

%以下是输入层至隐含层的权值调整
for i=1:1:5
dO(i)=4/(exp(I(i))+exp(-I(i)))^2;%(1*5矩阵)
end
segma=delta3*wo;%（1*5矩阵，行向量）
delta2 = dO.*segma;
d_wi = delta2'*xi+alfa*(wi_1-wi_2);
% 输入层-隐含层的加权系数调整
wi=wi_1+d_wi;

% 这里猜测存储的是历史信息？
wo_3=wo_2;
wo_2=wo_1;
wo_1=wo;%储存输出层本次调整后的权值

wi_3=wi_2;
wi_2=wi_1;
wi_1=wi;%储存隐层本次调整后的权值


Kp=K(1);Ki=K(2);Kd=K(3);
sys=[u_k,Kp,Ki,Kd];   

S函数完整代码附录

% 有个疑惑，到底是什么在选择flag？为什么这里没有主函数？
function [sys,x0,str,ts]=my_exppidf(t,x,u,flag)
switch flag,
    case 0,
        [sys,x0,str,ts]=mdlInitializeSizes;
    case 2,
        sys=mdlUpdates(x,u);
    case 3,
        sys=mdlOutputs(t,x,u);
    case {1,4,9},
        sys=[];
    otherwise
        error(['unhandled flag=',num2str(flag)]);%异常处理
end

% 模型初始化
function[sys,x0,str,ts]=mdlInitializeSizes
    sizes=simsizes;%用于设置模块参数的结构体用simsizes来生成
    sizes.NumContStates=0;%模块连续状态变量的个数
    sizes.NumDiscStates=3;%模块离散状态变量的个数
    sizes.NumOutputs=4;%模块输出变量的个数
    sizes.NumInputs=7;%模块输入变量的个数
    sizes.DirFeedthrough=1;%模块是否存在直接贯通，1表示存在直接贯通，若为0，则mdlOutputs函数里不能有u
    sizes.NumSampleTimes=1;%模块的采样时间个数,至少是一个
    sys=simsizes(sizes);%设置完后赋给sys输出
    x0=zeros(3,1);%系统状态变量设置
    str=[];
    ts=[0 0];%采样周期设为0表示是连续系统，
%     ts=[0.001 0];%采样周期设为0表示是连续系统，
function sys=mdlUpdates(x,u)
        T=0.001;
        x=[u(5);x(2)+u(5)*T;(u(5)-u(4))/T];%3个状态量（偏差、偏差和以及偏差变化量），u(5)是偏差，u(4)是上一次的偏差，x(2)则是之前的偏差和
        sys=[x(1);x(2);x(3)];
function sys=mdlOutputs(t,x,u)
            xite=0.2;
            alfa=0.05;
            IN=3;H=5;OUT=3;
            wi=rand(5,3);%产生一个5*3的随机数矩阵，随机数在（0，1）区间
            wi_1=wi;wi_2=wi;wi_3=wi;
            wo=rand(3,5);
            wo_1=wo;wo_2=wo;wo_3=wo;
            Oh=zeros(5,1);%产生一个1*5的零矩阵(行矩阵)
            I=Oh;
            xi=[u(1),u(3),u(5)];%神经网络训练的3个输入，期望值、误差以及实际值
            epid=[x(1);x(2);x(3)];%3个状态变量（偏差、偏差和、偏差变化量）（3*1矩阵，列向量）
            I=xi*wi';%隐层的输入
            for j=1:1:5
                Oh(j)=(exp(I(j))-exp(-I(j)))/(exp(I(j))+exp(-I(j)));%隐层的输出值（1*5矩阵）行矩阵
            end
            K1=wo*Oh;%输出层的输入（3*1矩阵）
            for i=1:1:3
                K(i)=exp(K1(i))/(exp(K1(i))+exp(-K1(i)));%得到输出层的输出（KP、KI、KD）（1*3矩阵，行向量）
            end
            u_k=K*epid;%计算得到控制律u，1个值
            %%以下是权值调整
            %隐含层至输出层的权值调整
            dyu=sign((u(3)-u(2))/(u(7)-u(6)+0.0001));
            for j=1:1:3
                dK(j)=2/(exp(K1(j))+exp(-K1(j)))^2; %输出层的输出的一阶导
            end
            for i=1:1:3
                delta3(i)=u(5)*dyu*epid(i)*dK(i);  %输出层的delta
            end
            for j=1:1:3
                for i=1:1:5
                    d_wo=xite*delta3(j)*Oh(i)+alfa*(wo_1-wo_2);
                end
            end
            wo=wo_1+d_wo;
            %以下是输入层至隐含层的权值调整
            for i=1:1:5
                dO(i)=4/(exp(I(i))+exp(-I(i)))^2;%(1*5矩阵)
            end
            segma=delta3*wo;%（1*5矩阵，行向量）
            delta2 = dO.*segma;
            d_wi = delta2'*xi+alfa*(wi_1-wi_2);
            wi=wi_1+d_wi;
            wo_3=wo_2;
            wo_2=wo_1;
            wo_1=wo;%储存输出层本次调整后的权值
            wi_3=wi_2;
            wi_2=wi_1;
            wi_1=wi;%储存隐层本次调整后的权值
         Kp=K(1);Ki=K(2);Kd=K(3);
         sys=[u_k,Kp,Ki,Kd];       

完整simulink模型（建议使用MATLAB2016b或更高版本）+S函数工程文件+原论文和思维导图xmind下载：
基于S函数的BP神经网络PID控制器及Simulink仿真和对应代码模型.zip

压缩包截图