学习笔记：粒子滤波的推导过程

前面的文章我们了解了到对于一个线性动态系统（比如说卡尔曼滤波）中的filtering问题可以用预测和跟新两个步骤求解，因为它们的后验概率和条件概率都服从高斯分布，所以比较容易求出解析解，但是对于非线性非高斯的动态系统，我们是无法求出其解析解的，那么这个时候该怎么做呢？于是人们就想到了借助采样的思想。

蒙特卡洛采样：

贝叶斯推断问题主要在于求解$P(z|x)$这个后验概率，但是这个后验概率不好求，于是蒙特卡洛就提出用采样的办法来近似等替后验概率。但是大多数应用中，我们更关心后验的期望，而不是后验的本身。后验的期望：$E_{z|x}[f(z)]=\int f(z)P(z)dx$，然后我们对后验P(Z)进行采样（采N个样本，$Z^{(i)}$~$P(z)$），那么上面的期望就可以近似为：$$E_{z|x}[f(z)]=\int f(z)P(z)dx\approx 1/N\sum _{i=1}^{n}f(z^{(i)})$$但是这里有个问题，就是说我们对后验$P(z)$进行采样是比较困难的，因为有些时候$P(z)$的维度很高等等，于是就有了下面的方法解决这个问题。

重要性采样

思想：引入一个已有的、相对比较简单的分布$q(z)$,我们把$q(z)$叫做提议分布，然后我们就从$q(z)$中进行采样。于是我们就有如下公式

其中$\frac{p(z^{(i)})}{q(z^{(i)})}$叫做权重，记为$w^{(i)}$，表示第i个样本权重。如果我们使用重要性采样的方法去解决filtering问题，那么我们就必须要求出t=1时刻到t=T时刻的权重:$w_t^{(i)}=\frac{p(z_t^{(i)}|x_{1:t})}{q(z_t^{(i)}|x_{1:t})}$ $w_1^{(1)},w_1^{(2)},...,w_1^{(n)}，w_2^{(1)},w_2^{(2)},...,w_2^{(n)}，...，w_T^{(1)},w_T^{(2)},...,w_T^{(n)}$
这样计算是非常麻烦，非常困难的。 那么我们就想能不能找到一个w的递推公式。我们就有了下面的新的采样方法。

Sequential Importance Sampling(SIS)采样

那么SIS是如何和找到$w_t^{(i)}和w_{t-1}^{(i)}$之间的关系呢？
SIS对filtering问题，它不关心$P(z_t|x_{1:t})$,它关心的是$P(z_{1:t}|x_{1:t})$（这样使计算方便）。那么对于$w_t^{(i)}\propto \frac{p(z_{1:t}|x_{1:t})}{q(z_{1:t}|x_{1:t})}$.递推公式如下：

SIS算法总结：用SIS求出了$w_t^{(i)}$之后，就可以将其带入重要性采样的那个期望公式中就可以算出期望值。

但是SIS也有一些问题，就是SIS在执行一定次数之后，它会出现权值退化的问题（权值越来越小）。也就会导致出现大量的权重小的粒子样本，而其他几个少量的粒子的权重又很大。对于这样的问题，我们的解决办法有两种：1）重采样 2）选择一个合适的提议分布$q(z)$

重采样

比如说我现在有三个样本以及它们的权重 $x^{(1)}=0.1,x^{(2)}=0.1,x^{(3)}=0.8$，然后我们画出他们的累积分布函数：

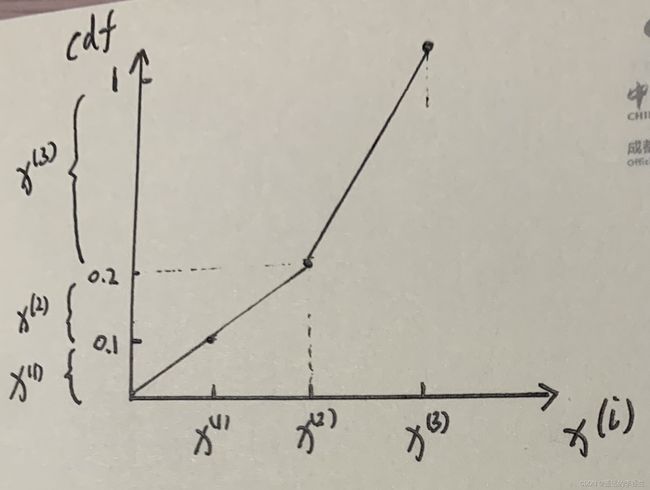
如图所示，我们在纵轴上面划分了三个区域，那么重采样是怎么样的呢？当我们在0-1这个区间随机采样的时候，如果样本点落到那个区域那么就把它划到哪个样本里面，比如说随机采样采到了0.3，那么就它把化为$x^{(3)}$这个样本区间里边，重采样后每个样本的权值都是相同的，比如重采样了N个样本，那么每个样本的权值就是1/N.到这里（这里介绍的重采样是最简单的一种），其实我们用上面所讲的SIS和重采样解决filtering问题的时候就相当于是一个最基本的粒子滤波了（SIS+Resampling）。

SIR滤波

前面我们说对于权值退化的问题，我们有两种方法，一个就是重采样，另一个就是选择一个好的$q(z)$，那么什么是好的$q(z)$呢？
一般我们选择$q(z_t\mid z_{1:t-1},x_{1:t})=p(z_t|z_{t-1})$，此时$z_t^{(i)}=p(z_t|z_{(t-1)}^{(i)})$
那么这个时候SIS算法中在计算权重的公式就会发生变化：

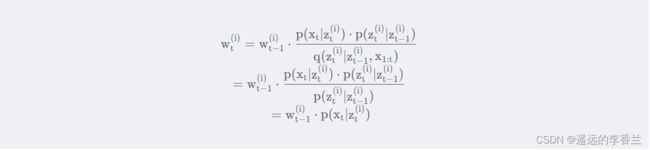
选择$q(z)$经过变换后的SIS就是SIR滤波。