模式识别— Fisher线性判别实验
模式识别— Fisher线性判别实验
一、实验目的:
1)加深对Fisher线性判别的基本思想的认识和理解。
2)编写实现Fisher线性判别准则函数的程序。
二、实验原理:
1.基本原理:
一般情况下,我们总可以找到某个方向,使得这个方向的直线上,样本的投影能分开的最好,而Fisher法所要解决的基本问题就是找到这条最好的、最易于分类的投影线。
先从d维空间到一维空间的一维数学变换方法。假设有一集合包含N个d维样本,其中个属于类的样本记为子集,个属于类的样本记为。若对的分量做线性组合可得标量
,
这样便得到N个一维样本组成的集合,并可分为两个子集和。的绝对值是无关紧要的,它仅使乘上一个比例因子,重要的是选择的方向,从而转化为寻找最好的投影方向,是样本分开。
2.基本方法:
先定义几个基本参量:
(1)各类样本均值向量
(2)样本类内离散度矩阵和总类内离散度矩阵
(3)样本类间离散度矩阵
我们希望投影后,在低维空间里个样本尽可能的分开些,即希望两类均值越大越好,同时希望各类样本内部尽量密集,即越小越好。因此,我们定义Fisher准则函数为
但不显含,因此必须设法将变成的显函数。
由式子
从而得到
,
采用Lagrange乘子法求解它的极大值
对其求偏导,得,即
从而我们很容易得到
忽略比例因子,得
这就是我们Fisher准则函数取极大值时的解。
三、实验内容:
依据实验基本原理和基本方法,对下面表3-1样本数据中的类别和计算最优方向,画出最优方向的直线,并标记出投影后的点在直线上的位置。选择决策边界,实现新样本xx1=(-0.7,0.58,0.089),xx2=(0.047,-0.4,1.04)的分类。
设某新类别数据如表3-2所示,用自己的函数求新类别分别和、分类的投影方向和分类阀值。
表3-1 Fisher线性判别实验数据
类别 1 2 3 4 5 6 7 8 9 10
x1 -0.4 -0.31 -0.38 -0.15 -0.35 0.17 -0.011 -0.27 -0.065 -0.12
x2 0.58 0.27 0.055 0.53 0.47 0.69 0.55 0.61 0.49 0.054
x3 0.089 -0.04 -0.035 0.011 0.034 0.1 -0.18 0.12 0.0012 -0.063
x1 0.83 1.1 -0.44 0.047 0.28 -0.39 0.34 -0.3 1.1 0.18
x2 1.6 1.6 -0.41 -0.45 0.35 -0.48 -0.079 -0.22 1.2 -0.11
x3 -0.014 0.48 0.32 1.4 3.1 0.11 0.14 2.2 -0.46 -0.49
表3-2 新类别实验数据
类别 1 2 3 4 5 6 7 8 9 10
x1 1.58 0.67 1.04 -1.49 -0.41 1.39 1.2 -0.92 0.45 -0.76
x2 2.32 1.58 1.01 2.18 1.21 3.61 1.4 1.44 1.33 0.84
x3 -5.8 -4.78 -3.63 -3.39 -4.73 2.87 -1.89 -3.22 -4.38 -1.96
四、实验程序及其说明:
1)Fisher准则函数算法:
其中w为我们要找到的投影方向,w1、w2是我们的样本、,s1、s2是相应样本的类内离散度矩阵,sw是总类内离散度矩阵,m1、m2是相应样本均值。在进行分别和、分类的投影方向和分类阀值时,将对应的s1、s2;sw;m1、m2以及输出坐标换成相应的样本符号。由于代码除此之外均相同,没有必要再重复列出,只需在运行时修改上述值即可。
注意:在画出w时(即),由于样本的不同,输出系数应作相应的调整。如:
、时,plot3(40x,40xw(2,:)/w(1,:),40xw(3,:)/w(1,:),‘k’);
、时,plot3(x,xw(2,:)/w(1,:),xw(3,:)/w(1,:),‘k’);
、时,plot3(5x,5xw(2,:)/w(1,:),5xw(3,:)/w(1,:),‘k’);
w1、w2fisher判别函数代码如下:
w1=[-0.4 -0.58 -0.089;-0.31 0.27 -0.04;-0.38 0.055 -0.035;-0.15 0.53 0.011;-0.35 0.47 0.034;
0.17 0.69 0.1;-0.011 0.55 -0.18;-0.27 0.61 0.12;-0.065 0.49 0.0012;-0.12 0.054 -0.063];
w2=[0.83 1.6 -0.014;1.1 1.6 0.48;-0.44 -0.41 0.32;0.047 -0.45 1.4;0.28 0.35 3.1;
-0.39 -0.48 0.11;0.34 -0.079 0.14;-0.3 -0.22 2.2;1.1 1.2 -0.46;0.18 -0.11 -0.49];
w3=[1.58 2.32 -5.8;0.67 1.58 -4.78;1.04 -1.01 -3.63;-1.49 2.18 -3.39;-0.41 1.21 -4.73;
1.39 3.61 2.87;1.2 1.4 -1.89;-0.92 1.44 -3.22;0.45 1.33 -4.38;-0.76 0.84 -1.96];
xx1=[-0.7 0.58 0.089];
xx2=[0.047 -0.4 1.04];
s1=cov(w1,1); %样本类间离散度S1
m1=mean(w1); %样本均值m1
s2=cov(w2,1); %样本类间离散度S2
m2=mean(w2); %样本均值m2
sw=s1+s2; %总类内离散度Sw
w=inv(sw)*(m1-m2)'; %Fisher
h1=figure(1);
for i=1:1:10 %打印样本。
plot3(w1(i,1),w1(i,2),w1(i,3),'r*');
hold on
plot3(w2(i,1),w2(i,2),w2(i,3),'bo');
end;
figure(2)
%画出fisher判别函数
xmin=min(min(w1(:,1)),min(w2(:,1)));
xmax=max(max(w1(:,1)),max(w2(:,1)));
x=xmin-1:(xmax-xmin)/ 100:xmax;
plot3(40*x,40*x*w(2,:)/w(1,:),40*x*w(3,:)/w(1,:),'k');
hold on
%将样本投影到fisher 判别函数上
y1=w'*w1';%yn=w'*T·*. xn.n=1,2
y2=w'*w2';
figure(2)
for i=1:1:10
plot3(y1(i)*w(1),y1(i)*w(2),y1(i)*w(3),'rx');
hold on;
plot3(y2(i)*w(1),y2(i)*w(2),y2(i)*w(3),'bp');
end;
w1、w3fisher判别函数代码如下:
w1=[-0.4 -0.58 -0.089;-0.31 0.27 -0.04;-0.38 0.055 -0.035;-0.15 0.53 0.011;-0.35 0.47 0.034;
0.17 0.69 0.1;-0.011 0.55 -0.18;-0.27 0.61 0.12;-0.065 0.49 0.0012;-0.12 0.054 -0.063];
w2=[0.83 1.6 -0.014;1.1 1.6 0.48;-0.44 -0.41 0.32;0.047 -0.45 1.4;0.28 0.35 3.1;
-0.39 -0.48 0.11;0.34 -0.079 0.14;-0.3 -0.22 2.2;1.1 1.2 -0.46;0.18 -0.11 -0.49];
w3=[1.58 2.32 -5.8;0.67 1.58 -4.78;1.04 -1.01 -3.63;-1.49 2.18 -3.39;-0.41 1.21 -4.73;
1.39 3.61 2.87;1.2 1.4 -1.89;-0.92 1.44 -3.22;0.45 1.33 -4.38;-0.76 0.84 -1.96];
xx1=[-0.7 0.58 0.089];
xx2=[0.047 -0.4 1.04];
s1=cov(w1,1); %样本类间离散度S1
m1=mean(w1); %样本均值m1
s2=cov(w3,1); %样本类间离散度S2
m2=mean(w3); %样本均值m2
sw=s1+s2; %总类内离散度Sw
w=inv(sw)*(m1-m2)'; %Fisher
h1=figure(1);
for i=1:1:10 %打印样本。
plot3(w1(i,1),w1(i,2),w1(i,3),'r*');
hold on
plot3(w3(i,1),w3(i,2),w3(i,3),'bo');
end;
figure(2)
%画出fisher判别函数
xmin=min(min(w1(:,1)),min(w3(:,1)));
xmax=max(max(w1(:,1)),max(w3(:,1)));
x=xmin-1:(xmax-xmin)/ 100:xmax;
plot3(x,x*w(2,:)/w(1,:),x*w(3,:)/w(1,:),'k');
hold on
%将样本投影到fisher 判别函数上
y1=w'*w1';%yn=w'*T·*. xn.n=1,2
y2=w'*w3';
figure(2)
for i=1:1:10
plot3(y1(i)*w(1),y1(i)*w(2),y1(i)*w(3),'rx');
hold on;
plot3(y2(i)*w(1),y2(i)*w(2),y2(i)*w(3),'bp');
end;
w2、w3fisher判别函数代码如下:
w1=[-0.4 -0.58 -0.089;-0.31 0.27 -0.04;-0.38 0.055 -0.035;-0.15 0.53 0.011;-0.35 0.47 0.034;
0.17 0.69 0.1;-0.011 0.55 -0.18;-0.27 0.61 0.12;-0.065 0.49 0.0012;-0.12 0.054 -0.063];
w2=[0.83 1.6 -0.014;1.1 1.6 0.48;-0.44 -0.41 0.32;0.047 -0.45 1.4;0.28 0.35 3.1;
-0.39 -0.48 0.11;0.34 -0.079 0.14;-0.3 -0.22 2.2;1.1 1.2 -0.46;0.18 -0.11 -0.49];
w3=[1.58 2.32 -5.8;0.67 1.58 -4.78;1.04 -1.01 -3.63;-1.49 2.18 -3.39;-0.41 1.21 -4.73;
1.39 3.61 2.87;1.2 1.4 -1.89;-0.92 1.44 -3.22;0.45 1.33 -4.38;-0.76 0.84 -1.96];
xx1=[-0.7 0.58 0.089];
xx2=[0.047 -0.4 1.04];
s1=cov(w2,1); %样本类间离散度S1
m1=mean(w2); %样本均值m1
s2=cov(w3,1); %样本类间离散度S2
m2=mean(w3); %样本均值m2
sw=s1+s2; %总类内离散度Sw
w=inv(sw)*(m1-m2)'; %Fisher
h1=figure(1);
for i=1:1:10 %打印样本。
plot3(w2(i,1),w2(i,2),w2(i,3),'r*');
hold on
plot3(w3(i,1),w3(i,2),w3(i,3),'bo');
end;
figure(2)
%画出fisher判别函数
xmin=min(min(w2(:,1)),min(w3(:,1)));
xmax=max(max(w2(:,1)),max(w3(:,1)));
x=xmin-1:(xmax-xmin)/ 100:xmax;
plot3(5*x,5*x*w(2,:)/w(1,:),5*x*w(3,:)/w(1,:),'k');
hold on
%将样本投影到fisher 判别函数上
y1=w'*w2';%yn=w'*T·*. xn.n=1,2
y2=w'*w3';
figure(2)
for i=1:1:10
plot3(y1(i)*w(1),y1(i)*w(2),y1(i)*w(3),'rx');
hold on;
plot3(y2(i)*w(1),y2(i)*w(2),y2(i)*w(3),'bp');
end;
五、 实验结果及其说明:
Fisher线性判别算法输出结果:
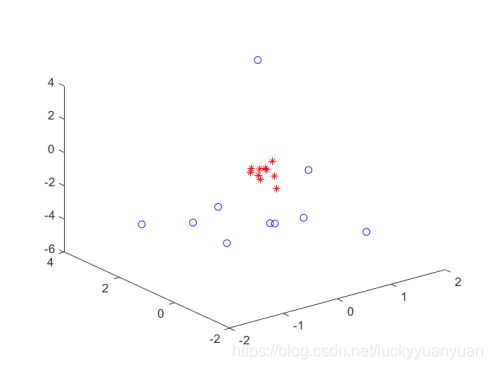
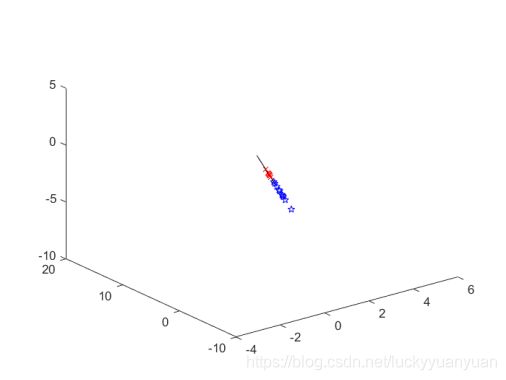
1.样本、及判别函数
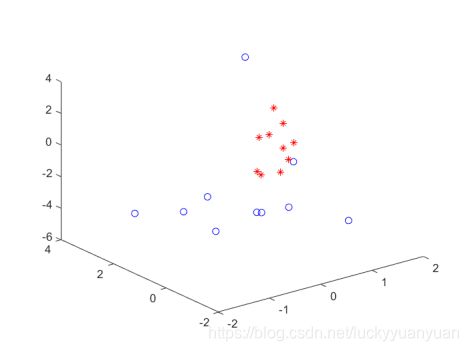
2.样本、及判别函数
六、实验小结:
模式识别实践课程加深了我们对Fisher线性判别的基本思想的认识和理解,通过仿照老师的程序,我们分别对w1和w2、w1和w3、w2和w3编写了计算最优方向,画出最优方向的直线,并标记出投影后的点在直线上的位置的程序,实现了Fisher线性判别准则函数。
我首先了解了Fisher线性判别的基本原理,和计算方法,w1和w2的实验,我模仿老师给的代码运行处w1和w2及其判别函数图像