基于MATLAB和模糊聚类分析的图像分类

基于MATLAB和模糊聚类分析的图像分类

在做数学建模校赛的时候，队伍选择了一道图像分类题，采用了模糊聚类分析的方法，这里记录下对这个方法的学习心得。

从本地导入文件

如下为从多张图片中提取出来的相同字符，本文将以“解”字为例，来进行讨论。

// ***处填入绝对路径
photo1= imread('C:\***\***\1.jpg');

调整图片灰度与亮度

先调整图片的灰度和亮度，方便下面的操作：

photo1_1 = imadjust(photo1, [0.2 0.5],[0 1],4);
M = stretchlim(photo1_1); 
photo1_2 = imadjust(photo1_1, M, [])；

查看调整前后的图片对比：

figure,
subplot(131),imshow(uint8(photo1));
subplot(132),imshow(uint8(photo1_1));
subplot(133),imshow(uint8(photo1_2));

结果如下：

进行灰度化处理

这里采用加权平均法进行处理

y1=1/3*photo1_2(:,:,1) + 1/3*photo1_2(:,:,2) + 1/3*photo1_2(:,:,3);

计算模糊相似矩阵

研究的样本总体为s张分辨率为mn的图像，对每张图像进行灰度化处理得到其相应的mn维灰度矩阵。

建立模糊相似矩阵R , 其中 ,r(p,q)为图像p与图像q的相似系数，表示两者的相似程度，这里采取绝对值减数法：

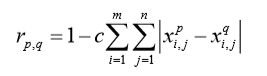
为了方便起见，先将28个二维矩阵，合并成一个三维矩阵

%合并矩阵为40*40*28
yy = zeros(40,40,28);
for i=1:28
yy(:,:,i) = eval(['y', num2str(i)]);
end

%计算模糊相似矩阵
R = zeros(28,28);
sum = 0;
for p=1:28
    for q = 1:28
    sum = 0;
        for i = 1:28
            for j = 1:28
                sum=sum+ abs(yy(i,j,p)-yy(i,j,q) );
            end
        end
        R(p,q)=1-sum*(1/1000000);
    end
end

%输出模糊相似矩阵
R

聚类

求得模糊相似矩阵之后进行聚类，先求得R的传递闭包，再选择适当的值来截取矩阵，截取规律如下，矩阵中大于等于该值的数取1，小于该值的数取0。

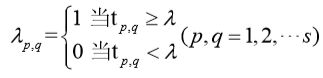
%求传递闭包
a=size(R);
B=zeros(a);
flag=0;
while flag==0  
  for i= 1: a  
    for j= 1: a
      for k=1:a
	%R与R内积，抄先取小再取大袭
	B(i,j) = max(min(R(i,k),R(k,j)),B(i,j)) ;   
      end
    end
  end
  if B==R
    flag=1;
  else
    R=B;%循环计算baiR传递闭du包
  end
end

截矩阵时有一个小技巧，先将二维矩阵拉成一维矩阵，再进行排序，从值较大的地方开始截取。

%求有多少个不相等数据
R1 = R;
R1 = R1(:); %拉成一维，
n = length(unique(B)); % 取唯一，算长度，可得要的不同值个数 
n %不同值的个数
R2 = unique(R1,'rows'); 

本文采取0.9638作为截取值。

RR = R;
for i =1:28
    for j = 1:28
        if RR(i,j)>=0.9638
           RR(i,j)=1；
           else
           RR(i,j) = 0;
        end
    end
end

当且仅当截取后的矩阵中对应的列向量相等，则其对应的样本可分为同一类。