数字图像处理习题(三)
数字图像处理习题(三)
文章目录
- 数字图像处理习题(三)
-
- 一、编程题
-
- 1. 图像的形态学处理
-
- 1.1 完成清华大学教材例9.10、9.11、9.30
-
- 1.1.1 例9.10 基于MATLAB编程,打开一幅二值图像进行开、闭运算。
- 1.1.2 例9.11 基于 MATLAB编程,对一幅二值图像进行矩形块和单向线段、交叉线段特征提取。
- 1.1.3 例9.30 基于 MATLAB编程,对灰度图像进行 Top-hat 变换和Bottom-hat变换。
- 1.2 比较灰度形态学开运算结果与重建开运算结果
- 2. 图像分割
-
- 2.1实现k-均值分割
- 3. 图像的特征提取
- 3.1 特征点提取(任选一种方法)、灰度共生矩阵(任选一种统计特征)、PCA变换提取第一主成分
-
- 3.1.1 Moravecs算法特征点提取
- 3.1.2 灰度共生矩阵(任选一种统计特征)
- 3.1.3 PCA变换提取第一主成分
一、编程题
1. 图像的形态学处理
1.1 完成清华大学教材例9.10、9.11、9.30
1.1.1 例9.10 基于MATLAB编程,打开一幅二值图像进行开、闭运算。
-
编程思路
(1)读取图片,并用
im2bw()函数将其转换为二值图像。(2)使用
strel(shape, parameters)创建一个方形的结构元素。 shape 是指定希望形状的字符串,参数parameters是指定形状信息的一系列参数,即
SE = strel('square', 10);创建一个10*10的正方形。(3)开运算是先腐蚀后膨胀。
imdilate(imerode(BW, SE), SE),也可以使用matlab自带的imopen(BW, SE)(4)闭运算是先膨胀后腐蚀。
imerode(imdilate(BW, SE), SE),也可以使用matlab自带的imclose(BW, SE) -
源代码
Homework1_1_1.m
%例9.10 基于MATLAB编程,打开一幅二值图像进行开、闭运算。 close all; clear; clc; Image = imread('img.jpg'); BW = im2bw(Image); %灰度图像转为二值图像 subplot(1,3,1),imshow(Image),title('原图'); SE = strel('square', 10); %创建方形结构元素 result1 = imdilate(imerode(BW, SE), SE); %先腐蚀后膨胀,即开运算 result2 = imerode(imdilate(BW, SE), SE); %先膨胀后腐蚀,即闭运算 subplot(1,3,2),imshow(result1),title('开运算'); subplot(1,3,3),imshow(result1),title('闭运算'); -
分析
(1)首先分析腐蚀与膨胀
-
膨胀算法:用结构元素,扫描二值图像的每一个像素,用结构元素与其覆盖的二值图像做“与”运算,如果都为0,结构图像的该像素为0,否则为1。结果:使二值图像扩大一圈。
膨胀后图像面积扩大,而且相邻的两个孤立成分有了连接。
-
腐蚀算法:用结构元素,扫描二值图像的每一个像素,用结构元素与其覆盖的二值图像做“与”运算,如果都为1,结构图像的该像素为1,否则为0。结果:使二值图像减小一圈。
目标集合中比结构元素小的成分被腐蚀消失了,大的成分面积缩小,并且其细连接处经过腐蚀后断裂。
(2)分析开运算,闭运算
-
根据腐蚀与膨胀的先后顺序可以实现开运算和闭运算。
-
**先腐蚀后膨胀,即开运算。**开运算一般能平滑图像的轮廓,削弱狭窄部分,去掉细长的突出、边缘毛刺和孤立斑点。
-
**先膨胀后腐蚀,即闭运算。**闭运算也可以平滑图像的轮廓,但与开运算不同,闭运算一般融合窄的缺口和细长的弯口,能填补图像的裂缝及破洞,所起的是连通补缺作用,图像的主要情节保持不变。
-
1.1.2 例9.11 基于 MATLAB编程,对一幅二值图像进行矩形块和单向线段、交叉线段特征提取。
-
编程思路
(1)用
imread()函数读取照片.(2)并用
graythresh()和im2bw()将原图转换为二值图像 ①
graythresh(image)函数输入是一副图像,输出就是阈值(TH)。这个函数使用最大类间方差法找到图片的一个合适的阈值(threshold)。 ② 再利用
im2bw(Imgage,TH)函数,将找到的阈值输入,就可以把原图变为一个二值图。(3)用
strel()函数创建结构元素,用imopen()函数进行开运算。 ① 利用
SE = strel('square',W)和创建方形结构元素,w为正方形边长(像素数)。用于矩形块提取。 ② 用
SE = strel('line', LEN, DEG)创建平坦的线型结构,LEN为长度,DEG为角度。用于线段提取。(3)因便于操作前期取反,所一在特征提取结束后需要再次取反,复原原图色彩。
-
源代码
Homework1_1_2.m
% 例9.11 基于 MATLAB编程,对一幅二值图像进行矩形块和有向线段特征提取。 close all; clear; clc; Image = imread('img3.png'); Th= graythresh( Image); OriginBW= im2bw(Image, Th); % 灰度图像转为二值图像 BW1=1-OriginBW; % 二值图像取反 se= strel('square',8); % 创建边长为8的正方形结构元素 BW2=1- imopen(BW1, se); % 用边长为8的正方形结构元素实现二值图像的形态开运算 se45=strel('line',23,45); % 创建长度为23,角度为45°的平坦线型结构元素 se135=strel('line',23,135); % 创建长度为23,角度为135°的平坦线型结构元素 BW3=1-imopen(BW1,se45); % 用长度为23,角度为45°的平坦线型结构元素实现二值图像的形态开运算 BW4=1-imopen(BW1,se135); % 用长度为23,角度为45°的平坦线型结构元素实现二值图像的形态开运算 BW5=1-imopen(BW1,se45)-imopen(BW1,se135); subplot(2,3,1),imshow(Image),title('原图'); subplot(2,3,2),imshow(OriginBW),title('二值图像'); subplot(2,3,3),imshow(BW2),title('矩形块提取'); subplot(2,3,4),imshow(BW3),title('45°有向线段提取'); subplot(2,3,5),imshow(BW4),title('135°有向线段提取'); subplot(2,3,6),imshow(BW5),title('交叉线段提取'); -
分析
(1)开运算是先腐蚀再膨胀,可以消除小物体或小斑块。原图经过开运算后,一些孤立的小点被去掉了。开运算能够去除孤立的小点,毛刺和小桥(即连通两块区域的小点),而总的位置和形状不变。
(2)程序运行结果的图片线段连续但宽度不均匀,是因为截取的是书上的图片,图片质量较差导致出现此情况。
1.1.3 例9.30 基于 MATLAB编程,对灰度图像进行 Top-hat 变换和Bottom-hat变换。
-
编程思路
(1)用
imread()函数读取照片,并用rgb2gray()函数将其转换为灰度图像。(2)用
se = strel('disk', 23);创建一个半径为23的圆盘结构元素,用imtophat()函数进行Top-hat变换;用imbothat()函数进行Bottom-hat变换。(3)用
imadjust()函数将图像进行灰度线性拉伸。 -
源代码
Homework1_1_3.m
%例9.30 基于 MATLAB编程,对灰度图像进行 Top-hat 变换和Bottom-hat变换。 close all; clear; clc; Image1 = rgb2gray(imread('img1.jpg')); Image2 = rgb2gray(imread('img2.jpg')); se = strel('disk', 23); %选取半径为23的圆盘结构元素 result1 = imtophat(Image1, se); result2 = imbothat(Image2, se); subplot(2,3,1),imshow(Image1);title('原始图像'); subplot(2,3,2),imshow(result1);title ('top-hat 变换'); %对图像Image1进行Top-hat变换 subplot(2,3,5),imshow(result2);title ('buttom-hat 变换'); %对图像Image2进行Bottom-hat变换 rr1 = imadjust(result1); %进行灰度线性拉伸 rr2 = imadjust(result2); %进行灰度线性拉伸 subplot(2,3,4),imshow(Image2);title('原始图像'); subplot(2,3,3),imshow(rr1);title('基于top-hat的对比度增强'); subplot(2,3,6),imshow(rr2);title('基于bottom-hat的对比度增强'); -
分析
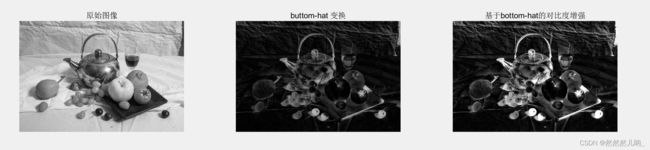
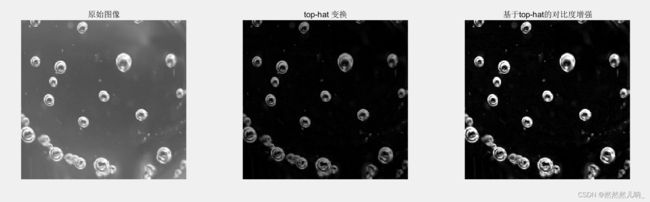
(1)程序运行结果如图所示。从图中可以看出Top-hat变换(顶帽变换)提取了图像中的亮细节分量。 Bottom-hat变换(低帽变换)提取了图像中的暗细节分量。
(2)另外:顶帽变换可以用于校正不均匀关照的影响。低帽变换可以突出比原图轮廓周围更暗的区域。
(3)最右侧是分别对两张图进行灰度线性拉伸的结果,实现了对比度增强的处理。效果体现更为明显。
1.2 比较灰度形态学开运算结果与重建开运算结果
-
编程思路
(1)读取图片。
(2)使用
strel(shape, parameters)创建一个方形的的结构元素。 shape 是指定希望形状的字符串,参数parameters是指定形状信息的一系列参数,即
se = strel('square', 12);创建一个12*12的正方形。形态学开运算(3)开运算:直接用
imopen()函数做开运算。 重建开运算:利用
imerode()函数对图像进行腐蚀,得到腐蚀图像。使用imreconstruct()函数,将腐蚀图像作为标记,利用原图像作为掩膜进行卷积运算。 -
源代码
Homework1_2.m
% 比较灰度形态学开运算结果与重建开运算结果 close all; clear; clc; Image = imread('img1.png'); se=strel('square', 12); % 创建方形结构元素 Image1=imerode(Image,se); % 腐蚀 Image2=imreconstruct(Image1,Image); % 由重构做开运算 Image3=imopen(Image,se); % 开运算 subplot(1,3,1),imshow(Image),title('原始图像'); subplot(1,3,2),imshow(Image2),title('重建开运算'); subplot(1,3,3),imshow(Image3),title('形态学开运算'); -
分析
(1)从结果看,开运算能平滑图像的轮廓,削弱狭窄部分,去掉细长的突出、边缘毛刺和孤立斑点。重建开运算可去掉孤立斑点,但不能去除细长的突出及边缘毛刺。
(2)开运算是对图像进行腐蚀之后再进行膨胀,可以消除小物体或小斑块,一般用来对图像的边缘进行平滑,腐蚀和膨胀所采用的的结构元素是相同的。详细说明见1.1.1。
(3)重建开运算是对图像先进行腐蚀,然后利用腐蚀所得到的图像作为标记,利用原图像作为掩膜进行卷积运算。从网上搜索资料发现重建开运算可以用来做车牌识别。
2. 图像分割
2.1实现k-均值分割
-
编程思路
(1)首先了解knn分类器的原理,创造样本简单实现knn分类器。(参考了网上的代码)
- 初始化训练集和类别;
- 计算测试集样本与训练集样本的欧氏距离;
- 根据欧氏距离大小对训练集样本进行升序排序;
- 选取欧式距离最小的前K个训练样本,统计其在各类别中的频率;
- 返回频率最大的类别,即测试集样本属于该类别。
(2)老师讲的课堂案例
(3)k-均值分割将图片分类。
-
源代码
Homework_2_1_1.m
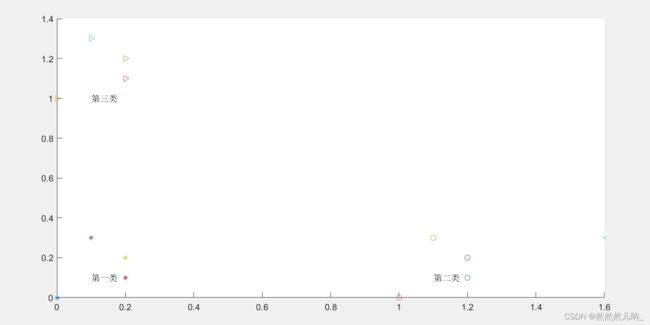
%实现KNN算法 %%算法描述 %1、初始化训练集和类别; %2、计算测试集样本与训练集样本的欧氏距离; %3、根据欧氏距离大小对训练集样本进行升序排序; %4、选取欧式距离最小的前K个训练样本,统计其在各类别中的频率; %5、返回频率最大的类别,即测试集样本属于该类别。 close all; clear; clc; %%算法实现 %step1、初始化训练集、测试集、K值 %创建一个三维矩阵,二维表示同一类下的二维坐标点,第三维表示类别 trainData1=[0 0;0.1 0.3;0.2 0.1;0.2 0.2];%第一类训练数据 trainData2=[1 0;1.1 0.3;1.2 0.1;1.2 0.2];%第二类训练数据 trainData3=[0 1;0.1 1.3;0.2 1.1;0.2 1.2];%第三类训练数据 trainData(:,:,1)=trainData1;%设置第一类测试数据 trainData(:,:,2)=trainData2;%设置第二类测试数据 trainData(:,:,3)=trainData3;%设置第三类测试数据 trainDim=size(trainData);%获取训练集的维数 testData=[1.6 0.3];%设置1个测试点 K=7; %%分别计算测试集中各个点与每个训练集中的点的欧氏距离 %把测试点扩展成矩阵 testData_rep=repmat(testData,4,1); %设置三个二维矩阵存放测试集与测试点的扩展矩阵的差值平方 %diff1=zero(trainDim(1),trianDim(2)); %diff2=zero(trainDim(1),trianDim(2)); %diff3=zero(trainDim(1),trianDim(2)); for i=1:trainDim(3) diff1=(trainData(:,:,1)-testData_rep).^2; diff2=(trainData(:,:,2)-testData_rep).^2; diff3=(trainData(:,:,3)-testData_rep).^2; end %设置三个一维数组存放欧式距离 distance1=(diff1(:,1)+diff1(:,2)).^0.5; distance2=(diff2(:,1)+diff2(:,2)).^0.5; distance3=(diff3(:,1)+diff3(:,2)).^0.5; %将三个一维数组合成一个二维矩阵 temp=[distance1 distance2 distance3]; %将这个二维矩阵转换为一维数组 distance=reshape(temp,1,3*4); %对距离进行排序 distance_sort=sort(distance); %用一个循环寻找最小的K个距离里面那个类里出现的频率最高,并返回该类 num1=0;%第一类出现的次数 num2=0;%第二类出现的次数 num3=0;%第三类出现的次数 sum=0;%sum1,sum2,sum3的和 for i=1:K for j=1:4 if distance1(j)==distance_sort(i) num1=num1+1; end if distance2(j)==distance_sort(i) num2=num2+1; end if distance3(j)==distance_sort(i) num3=num3+1; end end sum=num1+num2+num3; if sum>=K break; end end class=[num1 num2 num3]; classname=find(class(1,:)==max(class)); fprintf('测试点(%f %f)属于第%d类',testData(1),testData(2),classname); %%使用绘图将训练集点和测试集点绘画出来 figure(1); hold on; for i=1:4 plot(trainData1(i,1),trainData1(i,2),'*'); plot(trainData2(i,1),trainData2(i,2),'o'); plot(trainData3(i,1),trainData3(i,2),'>'); end plot(testData(1),testData(2),'x'); text(0.1,0.1,'第一类'); text(1.1,0.1,'第二类'); text(0.1,1,'第三类');Homework2_1_2.m
close all; clear; clc; img=imread('img.jpg'); label=textread('img-10.21op7-p-220t000-resized.regions.txt'); %imgl=reshape(img(:,:,2),320*240,1); se1=strel('disk',3); img_erode=imerode(img, se1); img_reop=imreconstruct(img_erode,img);img_stack=cat(3,img,img_reop); subplot(1,3,1),imshow(img,[]); subplot(1,3,2),imshow(label,[]); % imgl=reshape(img_reop,320+240,3); % imgl=reshape(img,320*240,3); imgl=reshape(img_stack,320*240,6); lab1=reshape(label,320*240,1); % predictlab=knnclassify(imgl,img1,lab1, 5); mdl = fitcknn(imgl,lab1,'NumNeighbors',5);%k为对应的1,2,3,4..... predictlab = predict(mdl,imgl); accuracy=length(find(predictlab==lab1))/length(lab1)*100; subplot(1,3,3),imshow(reshape(predictlab, 320,240),[]);Homework2_1_3.m
close all; clear; clc; org = imread('img.jpg'); %读入图像 figure; subplot(1,5,1); imshow(org),title('原始图像'); %显示原图像 % 接下来需要知道图片的尺寸(长和宽),如若直接对RGB图像进行操作,如下 % [m,n,p]=size(org) %m,n为所求,p=3为通道数 % 或者用下面的这种方法,转化为灰度图再求 gray=rgb2gray(org); [m,n]=size(gray); % 将图像进行RGB——3通道分解 % org(:, :, 1)......分别代表rgb通道 A = reshape(org(:, :, 1), m*n, 1); B = reshape(org(:, :, 2), m*n, 1); C = reshape(org(:, :, 3), m*n, 1); data = [A B C]; % r g b分量组成样本的特征,每个样本有三个属性值,共width*height个样本 % 第二张图 % kmeans第一个参数: N*P的数据矩阵,N为数据个数,P为单个数据维度 res = kmeans(double(data), 2); result = reshape(res, m, n); % 反向转化为图片形式 subplot(1,5,2); % label2rgb功能是转换标记矩阵到RGB图像 imshow(label2rgb(result)),title(strcat('K=',num2str(2),'时RGB通道分割结果')); % 显示分割结果 % 第三张图 res = kmeans(double(data), 3); result = reshape(res, m, n); subplot(1,5,3); imshow(label2rgb(result)),title(strcat('K=',num2str(3),'时RGB通道分割结果')); % 第四张图 res = kmeans(double(data),4); result = reshape(res, m, n); subplot(1,5,4); imshow(label2rgb(result)),title(strcat('K=',num2str(4),'时RGB通道分割结果')); % 第五张图 res = kmeans(double(data),5); result = reshape(res, m, n); subplot(1,5,5); imshow(label2rgb(result)),title(strcat('K=',num2str(5),'时RGB通道分割结果')); -
结果
Homework2_1_1.m
Homework2_1_2.m
Homework2_1_3.m
-
分析
(1)k均值聚类结果受到所选聚类中心的个数K和其初始位置以及模式样本的几何性质及读入次序等的影响。实际应用中需要试探不同的K值和选择不同的聚类中心起始值。
(2)我是直接用MATLAB里面的kmeans函数(官方文档有详细介绍),聚类起始点并不需要考虑。代码中我们重点关照一下K,并且把不同的K得出的效果放在同一个figure中,这样对比起来效果比较明显。
(3)其实这个样例分类分的还可以,但仍旧有些误差。可能是图片过于精细,图片内的内容院所过多,这种简单的分类不太容易区分。
(4)此外,比较有可能影响结果的应该就是模式样本的几何性质了,也就是图片的前景背景的占比,RGB占比等等。
3. 图像的特征提取
3.1 特征点提取(任选一种方法)、灰度共生矩阵(任选一种统计特征)、PCA变换提取第一主成分
3.1.1 Moravecs算法特征点提取
-
编程思路
(1)逐像素遍历, 计算垂直,水平,对角,反对角四个方向领域灰度差的平方和。
(2)四个方向中选最小值,做像素点的响应函数。
(3)设定一个阈值,将大于该阈值初次候选特征值的选为二次候选特征值。
(4)设定一个邻域,将该邻域最大的二次候选特征值作为最终要选择的特征值。
(5)若某点的CRF值大于某个阈值并为局部极大值时,则该像素点即为角点。
(6)焦点在图像中做标记,赋值为255.
-
源代码
Homework3_1_1.m
% Moravec角点检测 close all; clear; clc; img=double(imread('img4.jpg')); [h,w]=size(img); subplot(1,2,1),imshow(uint8(img)),title('原图'); imgn=zeros(h,w); n=4; for y=1+n:h-n for x=1+n:w-n sq=img(y-n:y+n,x-n:x+n); V=zeros(1,4); for i=2:2*n+1 %垂直,水平,对角,反对角四个方向领域灰度差的平方和 V(1)=V(1)+(sq(i,n+1)-sq(i-1,n+1))^2; V(2)=V(2)+(sq(n+1,i)-sq(n+1,i-1))^2; V(3)=V(3)+(sq(i,i)-sq(i-1,i-1))^2; V(4)=V(4)+(sq(i,(2*n+1)-(i-1))-sq(i-1,(2*n+1)-(i-2)))^2; end pix=min(V); %四个方向中选最小值 做像素点的响应函数 imgn(y,x)=pix; end end T=mean(imgn(:)); %设阈值,小于均值置零 ind=find(imgn<T); imgn(ind)=0; for y=1+n:h-n %选局部最大且非零值作为特征点 for x=1+n:w-n sq=imgn(y-n:y+n,x-n:x+n); if max(sq(:))==imgn(y,x) && imgn(y,x)~=0 img(y,x)=255;% 角点在图像中做标记 end end end subplot(1,2,2),imshow(uint8(img)),title('Moravec角点检测的图片'); -
大图
-
分析
(1)Moravec角点检测算法思路是以图像某个像素点(x,y)为中心,计算固定窗口内四个主要方向上(水平、垂直、对角线、反对角线)相邻像素灰度差的平方和,选取最小值作为像素点(x,y)的响应函数CRF;
(2)若某点的CRF值大于某个阈值并为局部极大值时,则该像素点即为角点。
3.1.2 灰度共生矩阵(任选一种统计特征)
-
编程思路
(1)matlab中的介绍
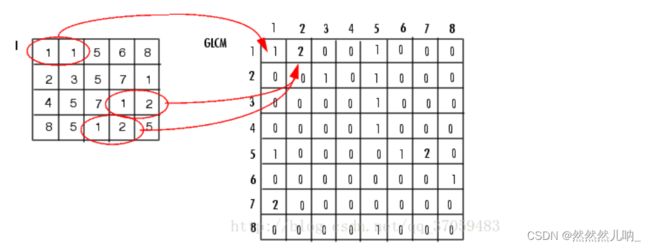
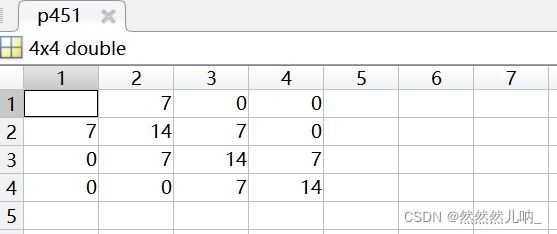
- 以(1,1)点为例,GLCM(1,1)值为1说明只有一对灰度为1的像素水平相邻。GLCM(1,2)值为2,是因为有两对灰度为1和2的像素水平相邻。(MatLab说明文档)
-
GLCM表其实就是所有像素可能的组合,比如,GLCM(1,1)就是I中像素值为1和1的组合,GLCM(4,5)就是I中像素4和像素5的组合,GLCM(i,j)的值呢就是I中像素为i,像素为j的有有多少和相邻的成对点。这个相邻有个规则:就是f(x,y),f(x+a,y+b)相邻,就是只有x相隔a的单位,y相隔b个单位,我们认为是相邻的。
-
平时我们说相邻:B点在A点右边,其实就是这里的a=1,b=0,也就是f(x,y)和f(x+1,y+0)相邻。
于是就有了:-
a=1,b=0 时我们就说水平相邻:也就是0度的时候
-
a=1,b=1 时我们就说对角相邻,也就是45度的时候
-
a=-1,b=1时 即135度
-
其他角度类似。
-
在a=1,b=0时:GLCM(1,1)=1;其实就是I中有几个1和1相邻(1个)(按上面的规则)GLCM(1,2)=2,几个1和2相邻(2个)。
-
-
源代码
Homework3_1_2.m
close all; clear; clc; IN1 = [ 0 0 1 1 2 2 3 3;0 0 1 1 2 2 3 3; 0 0 1 1 2 2 3 3;0 0 1 1 2 2 3 3;0 0 1 1 2 2 3 3;0 0 1 1 2 2 3 3;0 0 1 1 2 2 3 3;0 0 1 1 2 2 3 3]; IN2 = [ 0 1 2 3 0 1 2 3;1 2 3 0 1 2 3 0;2 3 0 1 2 3 0 1;3 0 1 2 3 0 1 2;0 1 2 3 0 1 2 3;1 2 3 0 1 2 3 0;2 3 0 1 2 3 0 1;3 0 1 2 3 0 1 2]; IN3 = [ 2 1 2 1 2 1 2 1;1 2 1 2 1 2 1 2;2 1 2 1 2 1 2 1;1 2 1 2 1 2 1 2;2 1 2 1 2 1 2 1;1 2 1 2 1 2 1 2;2 1 2 1 2 1 2 1;1 2 1 2 1 2 1 2]; [p451,p901] = comatrix(IN1,4); [p452,p902] = comatrix(IN2,4); [p453,p903] = comatrix(IN3,4);comatrix.m
%灰度共生矩阵函数 function[p45,p90] = comatrix(IN,gray) % gray 是灰度级个数,也是灰度共生矩阵的维数 g=gray; [R,C]=size(IN); p45 = zeros(g); p90 = zeros(g); %计算45°方向的共生矩阵 for M = 1:(R - 1) for N=2:C p45(IN(M,N)+1,IN(M + 1,N - 1)+1)=p45(IN(M,N)+1,IN(M + 1,N - 1)+1)+1; p45(IN(M+1,N - 1)+1,IN(M,N)+1)=p45(IN(M + 1,N - 1)+1,IN(M,N)+1)+1; end end %计算90°方向的共生矩阵 for M = 1:(R-1) for N=1:C p90(IN(M,N)+1,IN(M+1,N)+1)=p90(IN(M,N)+1,IN(M+1,N)+1)+1; p90(IN(M+1,N)+1,IN(M,N)+1)=p90(IN(M+1,N)+1,IN(M,N)+1)+1; end end end -
结果
-
分析
(1)灰度共生矩阵被定义为从灰度为i的像素点出发,离开某个固定位置(相隔距离为d,方位为)的点上灰度值为的概率,所有估计的值可以表示成一个矩阵的形式,以此被称为灰度共生矩阵。
(2)对于纹理变化缓慢的图像(分布较均匀的图像),其灰度共生矩阵对角线上的数值较大;而对于纹理变化较快的图像,其灰度共生矩阵对角线上的数值较小,对角线两侧的值较大。
(3)由于灰度共生矩阵的数据量过于庞大,一般不直接作为区分纹理的特征,而是基于它构建的一些统计量作为纹理分类特征。
(4)另外,Haralick曾提出了14种基于灰度共生矩阵计算出来的统计量:即:能量、熵、对比度、均匀性、相关性、方差、和平均、和方差、和熵、差方差、差平均、差熵、相关信息测度以及最大相关系数。这些信息量能更加直观的体现出图像。
3.1.3 PCA变换提取第一主成分
-
编程思路
(1)读取图片
(2)调用自定义的pca函数,提取图像的各主成分。
- 求各通道的均值
- 数据去中心化
- 求协方差矩阵
- 求特征向量与特征值
- 特征值和特征向量从大到小排序
(3)遍历结果将其显示出来。
-
源代码
Homework3_1_3.m
close all; clear; clc; %PCA 提取主成分 img = imread('img2.jpg'); subplot(2,2,1); imshow(img,[]);title('原图'); [width,length,heigth]=size(img); [vector,~,tempImg]= pca(img); PC = tempImg*vector; % 提取图像的各个主成分 for i = 1:heigth res = PC(:,i); min_value = min(res); max_value = max(res); res = reshape(res,[width,length]); str = sprintf('%s%d%s','第',i,'主成分'); subplot(2,2,i+1); imshow(res,[min_value,max_value]);title(str); endpca.m
function [vector ,value,tempImg] = pca(img) img=double(img)/255; [r ,c ,bands]=size(img); pixels = r*c; img = reshape(img, [pixels,bands]); tempImg = img; % 求各通道的均值 meanValue = mean(img,1); % 数据去中心化 img = img - repmat(meanValue,[r*c,1]); % 求协方差矩阵 correlation = (img'*img)/pixels; %求特征向量与特征值 [vector ,value] = eig(correlation); % 特征值和特征向量从大到小排序 vector = fliplr(vector); value = rot90(value,2); end -
结果
- 第一主成分
- 第一主成分
-
分析
(1)PCA是主成分分析。也是用于降维常用的一中方法。PCA 主要用于数据降维,对于高维的向量,PCA 方法求得一个 kk 维特征的投影矩阵,这个投影矩阵可以将特征从高维降到低维。
-
数据降维的目的:
- 减少预测变量的个数。
- 确保这些变量是相互独立的。
- 提供一个框架来解释结果。
- 降维后的特征向量减少冗余,具有低相关性等性质,在某些程度上反应了特征的本质,且在以后做分类预测等时,不容易陷入过拟合。
(2)PCA的一般用途:
- 聚类:把复杂的多维数据转为少量数据,易于分簇
- 降维:降低高维数据,简化计算,达到数据降维,压缩,降噪(去掉不太重要的特征)的目的
(3)PCA的作用:
-
将原有的d维数据集,转为k维数据,k
-
新生成的k维数据尽可能多的保留原来d维数据的信息,投影到对角线上的话,保留的数据信息会多一些。
-