机器学习预备02

相关分析（关联性分析）概述

什么是相关分析（关联性分析）

相关分析是用于考察变量间数量关系密切程度的分析方法，例如：

身高与体重的关系

10 几乎所有涉及到多个变量的假设检验方法，都可以被看作是这些变

量间的关联性分析

t 检验：分组变量与连续因变量间的关联性分析

卡方检验：行、列分类变量间的关联性分析

聚类分析：案例 (case) 间的关联性分析

多变量回归：因变量和一组自变量间的关联性分析

各种相关系数

连续 vs 连续： Pearson 相关系数（双变量正态分布）；

Spearman 秩相关系数（不符合双变量正态分布）

有序 vs 有序： Gamma 系数、肯德尔相关系数等（例如：医生

级别与治疗效果的相关关系）；也可使用 Spearman 秩相关系数

无序 vs 无序：列联系数等（例如：民族与职业的关系）

基于卡方统计量进一步推导而来

无方向 0~1

OR/RR: 一类特殊的关联强度指标

连续 vs 分类： Eta( 本质上是方差解释度，即连续变量的离散度

有多少可以被另外的分类指标所解释 )

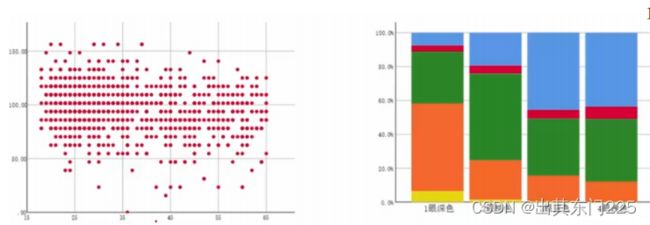
统计图 / 统计表在相关分析中的重要性

连续变量：用散点图先确认关联趋势是否为直线

分类变量：分组条图、马赛克图（分组百分条图）等工具

 

相关系数的计算原理

常用术语（针对两连续变量的相关）

直线相关：两变量呈线性共同增大，或者呈线性一增一减的情况

曲线相关：两变量存在相关趋势，但是为各种可能的曲线趋势

正相关与负相关：如果 A 变量增加时 B 变量也增加，则为正相

关，如果 A 变量增加时 B 变量减小，则为负相关

完全相关：完全正相关；完全负相关

零相关：自变量的变化 , 不会影响因变量的变化

Pearson 相关系数

计算公式

公式理解：标准差代表变量的离散程度（信息量大小）；

协方差 Cov(X,Y) 代表各变量共同携带的信息量大

小；

相关系数代表两个变量总信息量中的共同部分占比

相关系数 ρ 的取值范围： -1 < ρ < 1

其正负反映了相关的方向

| ρ | 越接近于 1 ，说明相关性越好

| ρ | 越接近于 0 ，说明相关性越差

Pearson 相关系数的检验：

H 0 : 两变量间无直线相关关系， ρ =0

检验方法： t 检验

Pearson 相关系数的适用条件：

必须是线性相关的情形（可以先绘制散点图观察一下）

针对两连续变量的相关系数

极端值对相关系数的计算影响极大，因此要慎重考虑和使用

要求相应的变量呈双变量正态分布（近似也可以）

 

Spearman 秩相关系数

不服从正态分布的变量、分类或等级变量之间的关联性可采用

Spearman 秩相关系数

Spearman 提出首先对数据做秩变换，然后再计算两组秩间的直

线相关系数（秩变换分析思想）

相关分析的 Python 实现

两个连续变量，且符合双变量正态分布： Pearson 相关系数

scipy.stats.pearsonr(a, b)

两个连续变量，不符合双变量正态分布： Spearman 秩相关系数

scipy.stats.spearmanr(a, b)

两个有序变量： Kendall's Tau ； Spearman 秩相关系数

scipy.stats.kendalltau(a, b) # 肯德尔相关系数
scipy.stats.spearmanr(a, b) # 斯皮尔曼秩相关系数

RR(Relative Risk)—— 相对危险度

表示两种情况下发病密度或者说发病概率之比

P t ：实验组人群反应阳性概率

P c ：对照组人群反应阳性概率

如果 RR > 1 ，说明相应的自变量取值增加，会导致个体发病 / 死

亡风险增加若干倍，

例如：吸烟者的发病概率是非吸烟者的 5 倍

RR 在医学中得到了极为广泛的应用

RR 的计算条件比较苛刻（观察周期长）

import numpy as np
import statsmodels.stats.contingency_tables as
tbl
# 这里必须使用np.array函数进行数组转换，否则后续计算会
出问题
table =
tbl.Table2x2(np.array(pd.crosstab(home.Ts9,
home.O1)))
print(table.oddsratio) # OR值
print(table.summary())  # 汇总信息