hdu 2604 Queuing AC自动机构造递推式->矩阵->结果

http://acm.hdu.edu.cn/showproblem.php?pid=2604

题意：

L个人排队，这一队里男性用m表示，女性用f表示，问长度为L的序列里面不包含形如"fmf"和"fff"的可能的排队的数量：

AC大牛的图：

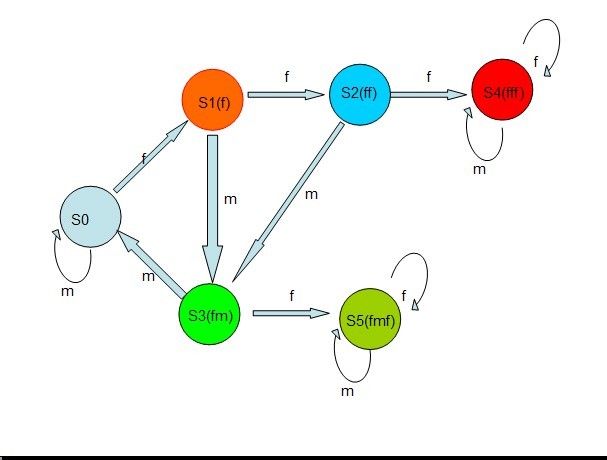
然后AC大牛给出了递推式：

S0表示其他状态
S1表示状态的后缀是(f),为了不和S2重复,姑且当成是(mf),其他状态同.
其他的图上应该很明确了.现在就是状态转移
显然在有后缀为fmf or fff以后后面无论加什么那么状态都不会变化了,于是
假设dp[i][j]表示长为i,后缀状态为j的方案数
dp[n][5]=2*dp[n-1][5]+dp[n-1][3]
dp[n][4]=2*dp[n-1][4]+dp-n-1][2]
dp[n][3]=dp[n-1][2]+dp[n-1][1]
dp[n][2]=dp[n-1][1]
dp[n][1]=dp[n-1][0]
dp[n][0]=dp[n-1][3]+dp[n-1][0]

我们构造矩阵

(f[n][5],f[n][4],f[n][3],f[n][2],f[n][1],f[n][0]) = {(201000),(020100),(000110),(000010),(000001),(001001)}*(f[n - 1][5],f[n - 1][4],f[n - 1][3],f[n - 1][2],f[n - 1][1],f[n - 1][0]);

然后利用矩阵快速幂求值然后再乘以(f[1][5],f[1][4],f[1][3],f[1][2],f[1][1],f[1][0])=(000011)即可：

//#pragma comment(linker,"/STACK:327680000,327680000")

#include <iostream>

#include <cstdio>

#include <cmath>

#include <vector>

#include <cstring>

#include <algorithm>

#include <string>

#include <set>

#include <functional>

#include <numeric>

#include <sstream>

#include <stack>

#include <map>

#include <queue>



#define CL(arr, val)    memset(arr, val, sizeof(arr))



#define lc l,m,rt<<1

#define rc m + 1,r,rt<<1|1

#define pi acos(-1.0)

#define ll long long

#define L(x)    (x) << 1

#define R(x)    (x) << 1 | 1

#define MID(l, r)   (l + r) >> 1

#define Min(x, y)   (x) < (y) ? (x) : (y)

#define Max(x, y)   (x) < (y) ? (y) : (x)

#define E(x)        (1 << (x))

#define iabs(x)     (x) < 0 ? -(x) : (x)

#define OUT(x)  printf("%I64d\n", x)

#define lowbit(x)   (x)&(-x)

#define Read()  freopen("din.txt", "r", stdin)

#define Write() freopen("dout.txt", "w", stdout);





#define M 23

#define N 1007

#define chN 50

using namespace std;



int n,m;

struct Mat

{

    int mat[6][6];

    void init()

    {

        CL(mat,0);

        mat[0][0] = mat[1][1] = 2;

        mat[0][2] = mat[1][3] = mat[2][3] = mat[2][4] = mat[3][4] = mat[4][5] = mat[5][2] = mat[5][5] = 1;

    }

}a;



Mat operator*(Mat a,Mat b)

{

    Mat c;

    int i,j,k;

    CL(c.mat,0);

    for (i = 0; i < 6; ++i)

    {

        for (j = 0; j < 6; ++j)

        {

            for (k = 0; k < 6; ++k)

            {

                if (!a.mat[i][k] || !b.mat[k][j]) continue;

                c.mat[i][j] += a.mat[i][k]*b.mat[k][j];

                if (c.mat[i][j] > m) c.mat[i][j] %= m;

            }

        }

    }

    return c;

}

Mat operator^(Mat a,int k)

{

    Mat c;

    int i,j;

    for (i = 0; i < 6; ++i)

    {

        for (j = 0; j < 6; ++j)

        {

            c.mat[i][j] = (i == j);

        }

    }

    while (k){

        if (k&1) c = c*a;

        k >>= 1;

        a = a*a;

    }

    return c;

}

int main()

{



//    Read();

    int i;

    while (~scanf("%d%d",&n,&m))

    {



        a.init();

        Mat res;

        res = a^(n - 1);

        int ans = 0;

        for (i = 2; i < 6; ++i)

        {

            ans += res.mat[i][4] + res.mat[i][5];

        }

        printf("%d\n",ans%m);



    }

    return 0;

}