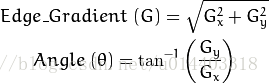(三)OpenCV中的图像处理之canny边缘检测和图像金字塔
注释:本文翻译自OpenCV3.0.0 document->OpenCV-Python Tutorials,包括对原文档种错误代码的纠正
3.7 canny边缘检测
3.7.1 目标:
- 学习OpenCV中的canny边缘检测
- 学习这些函数:cv2.Canny()
3.7.2 原理
Canny边缘检测是一种有效检测边缘的算法。它是由John F. Canny于1986年开发的。它是一个多阶段算法,我们来看看每个阶段。
1)降噪
由于边缘检测对噪声敏感,所以第一步是用5*5的高斯滤波器去除图像中的噪声。这在前面已有提到过。
2)寻找图像强度梯度
后用Sobel核在水平和垂直方向上过滤平滑图像,得到水平方向![]() 和垂直方向
和垂直方向![]() 上的一阶导数,然后在这两个图像中,我们可以找到每个像素的边缘梯度和方向如下:
上的一阶导数,然后在这两个图像中,我们可以找到每个像素的边缘梯度和方向如下:
梯度方向始终垂直于边缘。 它被四舍五入为表示垂直,水平和两个对角线方向的四个角度之一。
3)非最大抑制
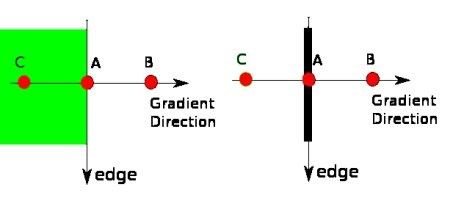
在获得梯度大小和方向后,要完成图像的全扫描以去除可能不构成边缘的任何不需要的像素。为此,在每个像素处,如果该像素沿梯度方向的邻域中的局部最大值,该像素会被检查。查看下图:
点A位于垂直方向的边缘上,点B和C在梯度下降的方向上,所以点B和点C会检查点A是否形成局部最大值,如果是,下一步操作会考虑点A,否则被置为0.
简而言之,您获得的结果是具有“薄边”的二进制图像。
4)滞后阈值
这一步是决定哪些边缘是真正的边缘而哪些不是。为此,我们需要两个阈值,minVal和maxVal,所有梯度值大于maxVal的边缘一定是边缘,而小于minVal的肯定不是边缘,因此被丢弃。介于minVal和maxVal的根据连接性分为边缘和非边缘,如果它们连接到“确定边缘”的像素,则认为是边缘,否则被丢弃。
边缘A在maxVal之上,因此被视为确定边缘,虽然边缘C在maxVal之下,但它连接到边缘A因此也被视为有效边缘,并且我们得到该完整曲线。但边缘B虽然高于minVal并且与边缘C的区域相同,但是它没有连接到任何“肯定边缘”,因此被丢弃。所以非常重要的是我们必须相应地选择minVal和maxVal才能得到正确的结果。
假设边缘是长线,这个阶段也会消除小像素的噪音。所以我们终于得到的是图像中的强度。
3.7.3 OpenCV中的canny边缘检测
OpenCV将上述所有过程都集成在方法cv2.Canny()中,该函数的第一个参数是输入图像,第二个和第三个参数分别是minVal和maxVal,第四个参数是aperture_size,用于查找图像梯度的Sobel内核的大小。默认情况下是3。最后一个参数是L2gradient,它指定查找梯度大小的方程。
代码示例:
# -*- coding: utf-8 -*-
'''
canny边缘检测:
1.降噪:边缘检测对噪声敏感,所以第一步用5*5的高斯核去除噪声
2.寻找图像强度梯度:使用Sobel核在水平和垂直方向上过滤图像,得到水平和垂直方向上的一阶导数
3.非最大抑制:获得梯度大小和方向后,要完成图像的全扫描去除不可能构成边缘的任何不需要的像素
(为此,在每个像素处,如果该像素沿梯度方向的领域中的局部最大值,该像素会被检查)
4.滞后阈值:这一步决定哪些是真的边缘哪些不是
cv2.Canny(img,minval,maxVal,aperture_size,L2gradient)
'''
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('2.jpg', 0)
edges = cv2.Canny(img, 100, 200)
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Original Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(edges, cmap='gray')
plt.title('Edge Image'), plt.xticks([]), plt.yticks([])
plt.show()
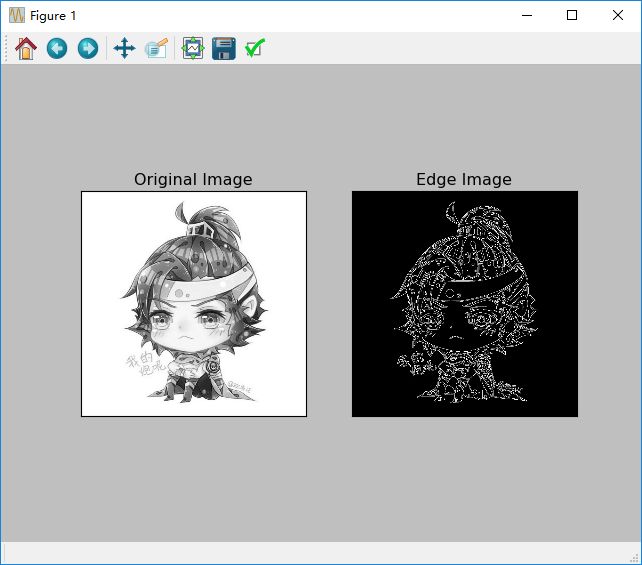
结果:
3.8 图像金字塔
3.8.1 目标:
- 学习图像金字塔
- 学习用图像金字塔创造水果"Orapple"
- 学习这些函数:cv2.pyrUp()、cv2.pyrDown()
3.8.2 原理
正常情况下,我们处理的是大小不变的图像,但有时候,我们需要处理不同分辨率下的同一张图像。例如,在图像中寻找某物的时候,我们不确定图像中的对象以什么样的大小显示。在这种情况下,我们需要创建一组不同分辨率的图像,并在所有图像中搜索该对象。这些具有不同分辨率的图像称作图像金字塔(因为当它们堆叠在一起,分辨率最大的图像在最底部,分辨率最下的图像在最顶端)。
这里有两种类型的金字塔:1)高斯金字塔2)拉普拉斯金字塔
高斯金字塔中高层(低分辨率)是通过删除低层(高分辨率)中图像的连续行和连续列得到的。然后,较高层中的每个像素由基础级别中的5个像素与高斯权重的贡献形成。通过这样做,一个图像成为图像。因此,面积减少到原始面积的四分之一。它被称为八度。我们在金字塔上升(即分辨率降低)时相同的模式继续下去。类似地,在扩展时,每个层面的面积变成4倍。我们可以使用cv2.pyrDown()和cv2.pyrUp()函数得到高斯金字塔。
拉普拉斯金字塔由高斯金字塔形成。没有排他的功能。 拉普拉斯金字塔图像仅仅是边缘图像。 它的大多数元素都是零。 它们用于图像压缩。拉普拉斯金字塔中的一个层是由高斯金字塔的高低层与高斯金字塔上层扩展版本之间的差异形成的。
3.8.3 用金字塔进行图像融合
金字塔的一个应用是图像融合。例如,在图像拼接中,需要将两个图像堆叠在一起,但由于图像之间的不连续性,效果看起来会不太好。在这种情况下,图像金字塔就可以让图像无缝衔接,而不会在图像中留下大量数据。一个典型的栗子就是混了了两个水果,橙子和苹果。实现图像的融合只需完成如下操作:
1) 加载橘子和苹果的图像
2) 得到橘子和苹果的高斯金字塔(在该例中,数量是6)
3) 从高斯金字塔中,得到它们的拉普拉斯金字塔
4) 在拉普拉斯金字塔的各层中,左边加入苹果,右边加入橘子
5) 最后从这个联合图像金字塔中,重建原始图像
代码如下:
# -*- coding: utf-8 -*-
'''
图像金字塔:
1.两种类型的金字塔:1)高斯金字塔2)拉普拉斯金字塔
2.使用cv2.pyrDown()和cv2.pyrUp()得到高斯金字塔
3.拉普拉斯金字塔中的一层由高斯金字塔的高低层与高斯金字塔上层扩展版本之间的差异形成
4.金字塔的一个应用是融合:例如,图像拼接中,需要将两个图像堆叠在一起,但由于图像之间的
不连续性,效果看起来会不太好。在这种情况下,图像金字塔就可以让图像无缝衔接,而不会在图像中
留下大量数据。
'''
import cv2
import numpy as np
import warnings
from matplotlib import pyplot as plt
warnings.filterwarnings("ignore", category=np.VisibleDeprecationWarning)
A = cv2.imread('orange.jpg')
B = cv2.imread('apple.jpg')
# 生成A的高斯金字塔
G = A.copy()
gpA = [G]
for i in range(6): # 生成A的6层高斯金字塔
G = cv2.pyrDown(G)
gpA.append(G)
# 生成B的高斯金字塔
G = B.copy()
gpB = [G]
for i in range(6): # 生成B的6层高斯金字塔
G = cv2.pyrDown(G)
gpB.append(G)
# 生成A的拉普拉斯金字塔
lpA = [gpA[5]] # lpA赋值A高斯金字塔尖端,也就是最小段
for i in range(5, 0, -1): # 从A金字塔最尖端往上遍历
GE = cv2.pyrUp(gpA[i]) # 在高斯金字塔图层生成拉普拉斯金字塔
L = cv2.subtract(gpA[i - 1], GE) # 此处需要注意,如果图片分辨率连续除6次2,不能整除,代码会报错,此处是矩阵相加需要矩阵行列长度都相等
lpA.append(L) # 添加进拉普拉斯金字塔
# 生成B的拉普拉斯金字塔
lpB = [gpB[5]] # lpB赋值B高斯金字塔尖端,也就是最小段
for i in range(5, 0, -1):
GE = cv2.pyrUp(gpB[i])
L = cv2.subtract(gpB[i - 1], GE)
lpB.append(L)
# 现在在每一层中添加左右半边图像
LS = []
for la, lb in zip(lpA, lpB): # 利用zip把所有拉普拉斯金字塔变成List
rows, cols, _, = la.shape
ls = np.hstack((la[:, 0:cols / 2], lb[:, cols / 2:])) # A和B各半边按列对接
LS.append(ls)
# 现在重构
ls_ = LS[0] # 赋值金字塔最小端
for i in range(1, 6): # 从小到大将对接好的图恢复为大图
ls_ = cv2.pyrUp(ls_)
ls_ = cv2.add(ls_, LS[i])
# 直接连接每一半的图像
real = np.hstack((A[:, :cols / 2], B[:, cols / 2:])) # 原图各半对接用来对比
cv2.imwrite('Pyramid_blending2.jpg', ls_)
cv2.imwrite('Direct_blending.jpg', real)
# cv2.imshow('pyramid', ls_)
# cv2.imshow('direct', real)
titles = ['orange', 'apple', 'directMerge', 'pyramidMerge']
images = [A, B, real, ls_]
for i in range(4):
plt.subplot(2, 2, i + 1), plt.imshow(images[i]), plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
# cv2.waitKey(0) & 0xFF
# cv2.destroyAllWindows()
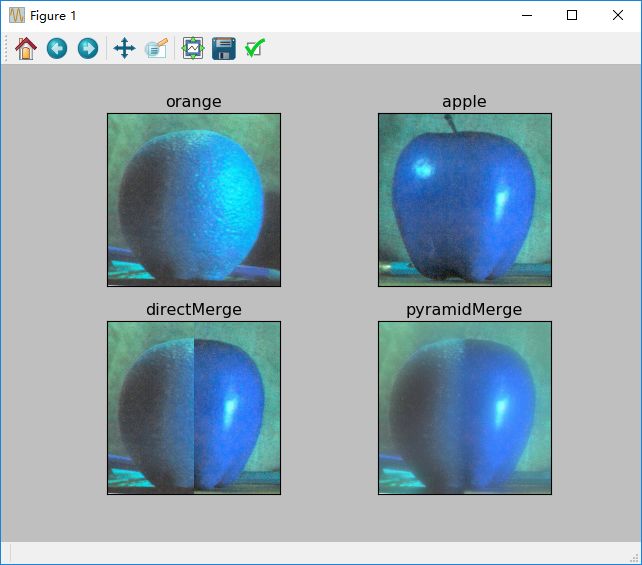
结果如下:图一、二是原始图像,三是直接拼接,四是图像金字塔拼接