GNN、GCN原理及推导

在这里插入图片描述
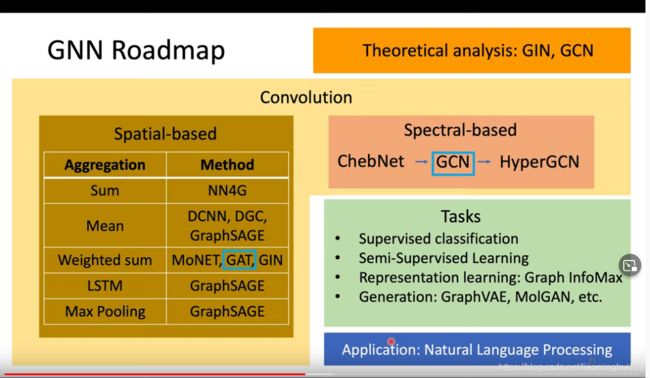
GNN分为两个角度去研究，一个空间域，一个谱域。

Spatial-based Conovolution

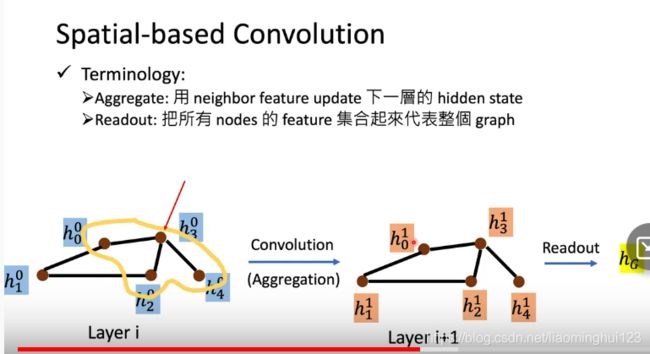
空间域的卷积就是空间上的卷积，跟CNN很像，就是综合一个节点的邻接节点的特征用来生成下一层的该点的特征然后整合成下一层的图：

1,NN4G

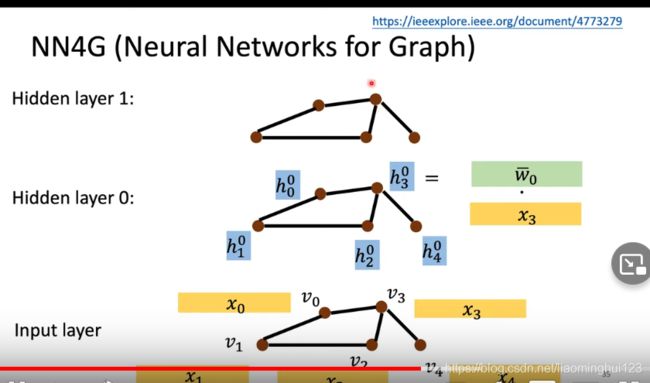
如上图，这里的卷积就是，对于v3来说，下一层的V3的特征就是一个参数（矩阵）乘以这一层的邻接点的特征，然后加上自己的特征与一个参数矩阵的乘积之后的输出跟CNN不一样，输出的y是前面所有层的平均然后分别乘以可训练矩阵后加起来得到：
为什么相加呢？可能是每一个节点的邻居数目都不一样，用相乘的话系数不统一。
2，DCNN
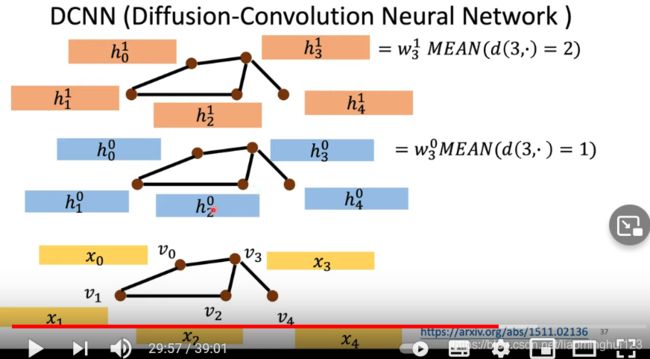DCNN的每一层都是以原始的数据进行更新，对于V3来说，第一层就是对和V3邻接为一的节点的特征（都是原始的特征）都加起来然后取平均乘以权重系数，第二层是取和它距离为2的节点特征（都是原始的）取平均然后乘以权重系数。
这样得到很多层的节点特征以后，把H都串起来乘以一个权重矩阵得到y：
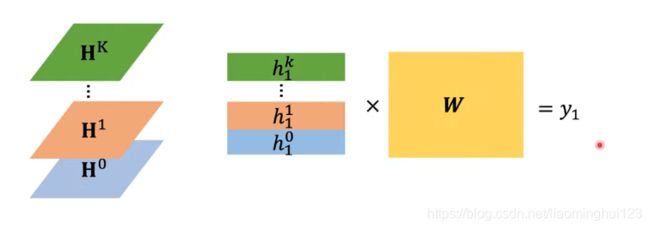3，MoNET
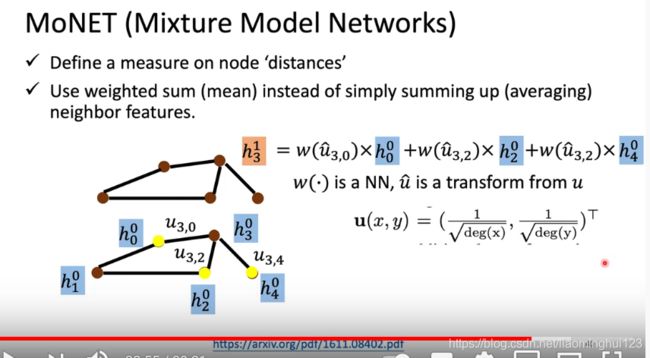这是考虑到权重而不是简单的相加，权重是由他们的度决定的，得到u后乘以一个矩阵变化成u一撇。
4，GraphASGE
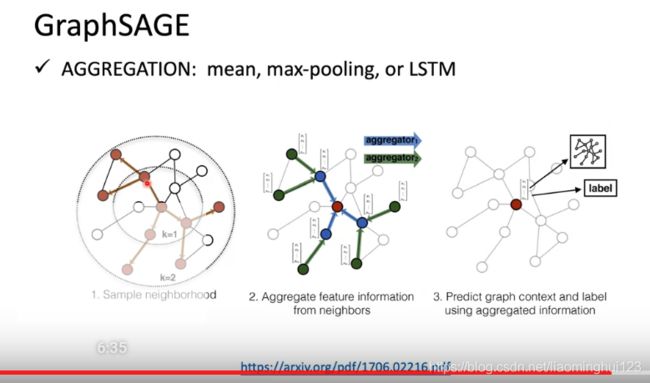5，GAT
GAT就是要对它的邻居做attention，得到e:

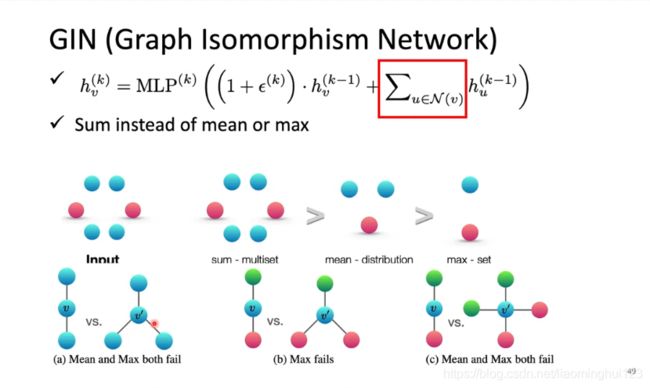
6, GIN
以上论文提出，我们在update的时候，下一层应该是对上一层的求和，然后再加上自己的上一层乘以一个东西，这里的epsion也可以等于0。之所以用sum而不用max-pool或者mean-pool是因为它对一些情况有更好的分辨（用多层MLP而不是一层）：

Spectral-based GCN

CNN可以用一个特定大小的过滤器来卷积，但是GNN不行，因为每个节点的邻居都不一样。所以要把图在空间的结构转化一下思想，再另一个域实现类似的过滤器来卷积，这就是谱域。这个过程用下面的图来说明：
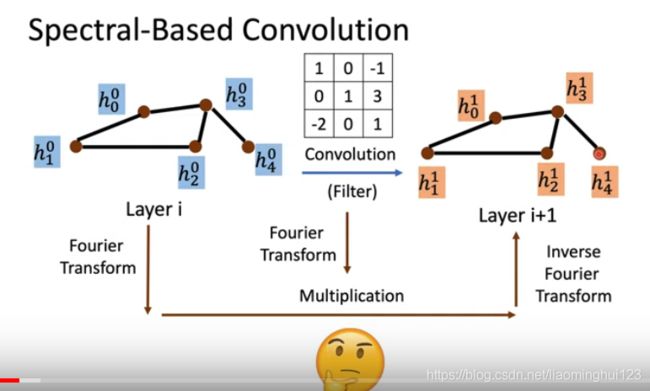那么要怎么经过这个傅里叶变换呢？先来补充一下信号系统的知识。

信号与系统相关

一个信号可以看做是n维空间的向量A，它可以看做是一组基向量vi的线性组合：

这个叫合成，此时求某一个基向量的大小（占比），就要用到分析，分析是信号和这个基向量做内积：

我们知道cos和sin是常用的基向量。
现在对于一个周期性信号X(t)，我们 可以把他看做是很多（无穷个）傅里叶基向量乘以他们分别的占比ak所合成的：

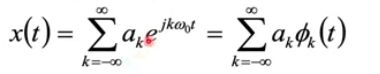
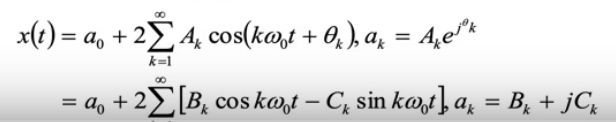
一组信号可以在不同的域用不同的基来表示/合成，这里给出时域和频域的两种合成：


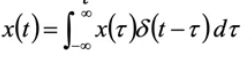
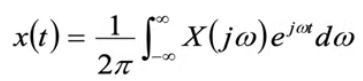
现在我们的要做的内容就是要做分析：

Spectral Graph Theory

图信号的傅里叶变换

符号表示：
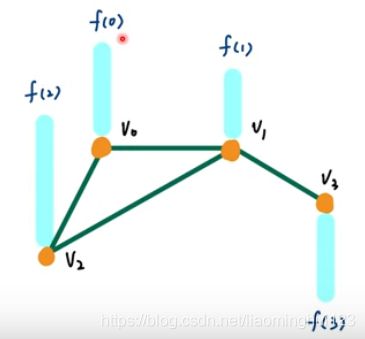
在如下的图中，我们把f看做是一个信号，比如f(0)，它可以是一个向量也可以是一个标量（此文中假定f(0)等4个信号都是标量），假设节点是城市的话，f可以看做是这个城市的人口什么的特征：
首先定义拉普拉斯矩阵L=D-A，它是半正定矩阵，即所有的特征值都不小于0，且具有对称的性质，特征值分解可以得到：
特征值λ是频率，对应的u是对应的基向量。
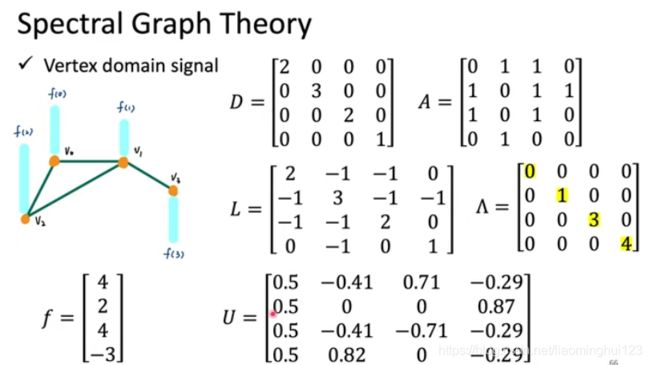如上图，左边是构成的图，这个f=[f(0),f(1),f(2),f(3)]^T。计算出L后进行特征值分解得到U和λ。λ1=0对应的U的第一列，同理后面的对应的U的每一列。
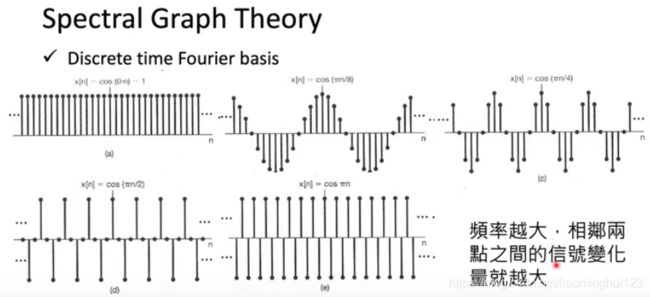
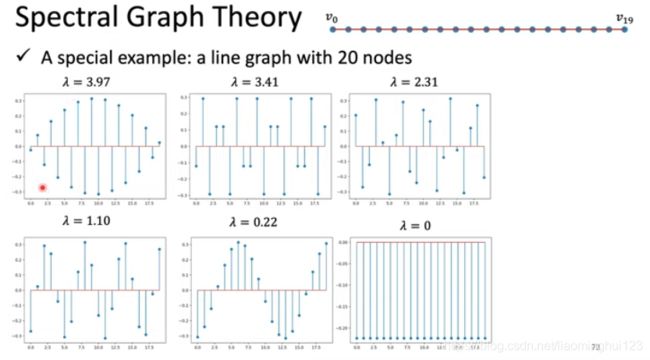
λ可以看做是频率，越低频，对应的特征向量（可以衍射在图中）越光滑：
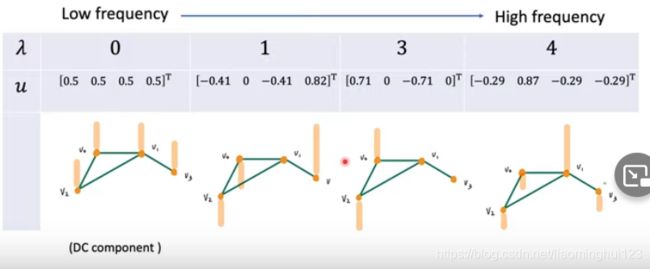从下图中可以看出来频率越大，相邻节点的的变化量越大，在右下图已经完全正负相反了：

我们现在来做一件这样的事，Lf=（D-A）f = Df - Af：
我们首先来看Lf的第一个数是怎么来的，是：黄色的框里面有个2，这个2代表的是节点0有2个和它相接的邻居，这个两个邻居分别可以从红框里的1,1看到是第1个和第2个节点；然后黄框里唯一的非零2会乘上自己的信号大小4，再分别减去和他相邻的两个节点的大小2，和4；所以这个a的物理意义就是它和它所有相接的领点的信号大小的差的总和，也就是说这个a如果越大，那么此节点和周围邻点的信号差越大，信号在这里越不光滑。
上述要是想把Lf看成是“能量”的差异的话，在（4-2）和（4-4）（在上图最后一行的算式中）的运算中还要加上平方运算，平方运算就是f^TLf：
上式运算的结果就可以看做是点i和点j的“能量差”的，对他们所有点求和，其实就是表示图的信号的光滑度
，值越大越不光滑。
现在把f换成ui：

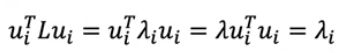
就是它的特征值！！！！！！！！！ 妙啊（编者按：有论文提到强制缩小λ而获得更光滑的特征也就是信号）
来看一个例子：
那么我们为什么要讲上面那些东西呢？其实就是因为图不能在空间域上定义一个稳定大小的filter，所以要尝试在另外一个域里定义一个filter。下图是一个传统的在时域上（类似于图的空间域）的信号，经过傅里叶变换得到在频域上的信号：

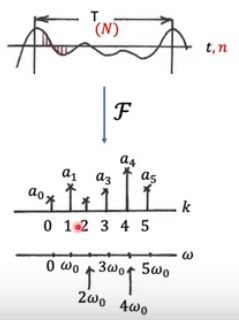
（如果大家忘了傅里叶变换的意义的话，这里给出一张动图

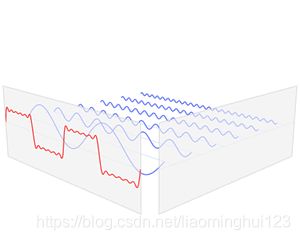
傅里叶变换的可可视化，图片来自于这里）
上上张图的a就是每一个频的振幅了。
现在同样的我们要把我们的图信号转到频域里：

x拔就是频域上的信号了。这个公式在做的事情就是前文所提到的分析：

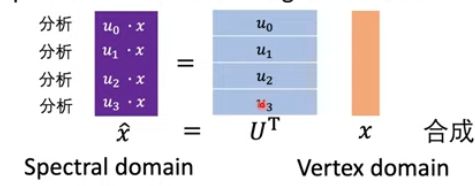
这里u0和X做点积就是求x中u0这个基向量的占比有多少，其他的ui同理。
所以我们就可以通过傅里叶变换把一个空间域的图信号转化为谱域上的信号：
在上图的左边，就是表示每一个不同频率（λi）成分上面他的大小（uif）是多少。是不是和传统的信号的在频域上面的表示（上图最右）很像了？
频域上还是不具有直观的效果，所以我们要想办法把在频域运算过的图信号转成空间域。首先看一下传统的信号是怎么从频域转到空间域的：
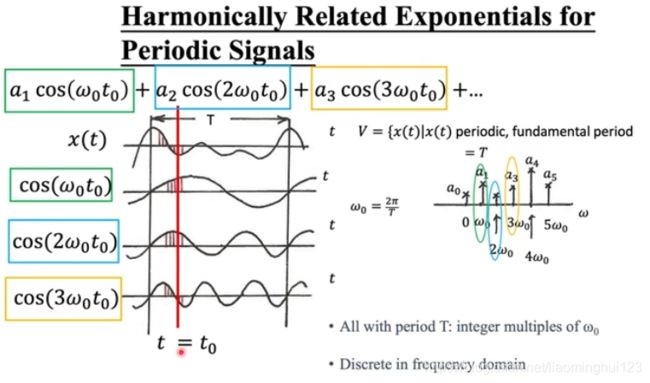上图可知，把不同频域的占比a乘以cos（该频域）然后对所有频域求和就是了。所以类似的，图信号转化为空间域就是要：不同频率（λ）上的信号大小（类比上面的cos(频率)）乘以这个频域上的信号占比uif（类比传统信号的ai）。比如现在开始求下图点v0的信号大小，更相同颜色圈圈里相乘然后相加，右边分布是对应的不同频域的信号大小：
在数学上表示就是：
其中x向量最上面的值就是节点0的信号大小，它是等于ui在0处的大小乘以ui的占总向量的占比ui*x。
到现在，图信号从空间域到谱域（类比传统的信号从时域到频域）、从谱域到空间域（类比传统的信号从频域到时域）已经讲完了。讲它的目的就是为了能在谱域上进行filter。下面开始讲filter。

Filter

在传统的信号的卷积上，如下（注意横轴和纵轴）：
现在要搞一个图信号的filter。如下图，右上的纵坐标是信号在λi上的大小uif，现在要给它一个频域响应函数gθ，经过这样的卷积之后，该λ处的信号大小就变成了y = g（λ）：
将上面的x^打开就是U ^Tx，然后在经过傅里叶逆变换(就是如前文所讲的用U去乘它)得到过滤的信号在空间域的表示：
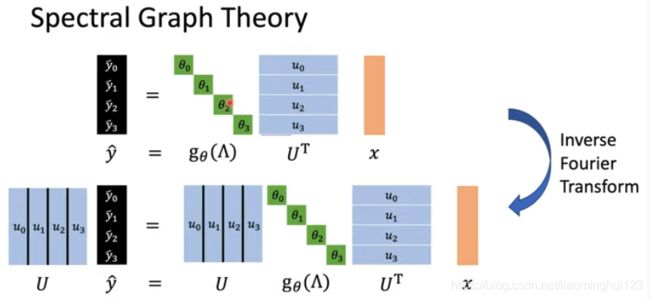现在经过卷积过的在空间域的信号y有了如下表达式：
上图中g是一个函数，θi是函数在λi上的值，该函数的参数是可学习的。根据矩阵的规则，把U和U^T放g的里面来，y就等于：

g（.）可以是任何函数，比如下面的：

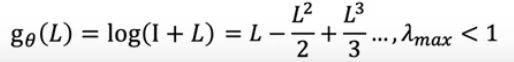
上面的函数，问题一：它的O(N)是不好的（不可能图不一样过滤器就不一样吧？那你构造的模型也不一样了），CNN都是固定的大小。
问题二：如果对于下面这个函数会怎么样呢？:

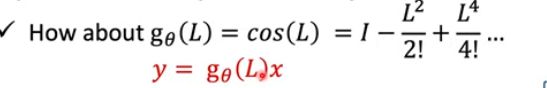
为了解释上图这个函数合不合理，我们首先看这样的函数：

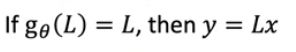
那么在这样的图中:

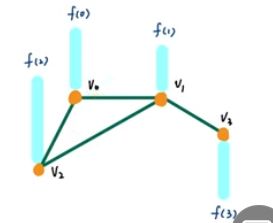
它的表现是：

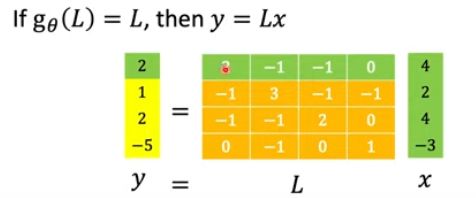
我们可以看到这样的过滤后的v0的信号大小y(0)=2是由上图的绿色区域点积形成，在L的右上角是为0的，这是因为点0和点3没有直接相连。那么如果是g（L）=L^2会怎么样呢？
是如下：
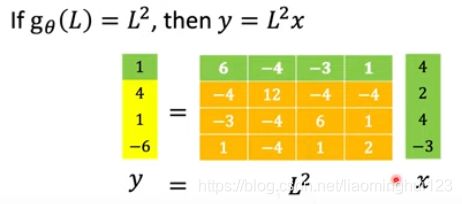L^2看到所有的节点都是非0了，这是因为点0经过1次跳跃可以达到节点3了。多少次方就是多少次跳跃连接。 所以L^N会被所有的点影响，但是这不是我们想要的，它不是localize （CNN的filter就是localize，它可以决定感受野的大小）。

ChebNet

ChebNet是谱域卷积的第一个model。
如上图，它是一个k-localized，而且求参数的时候是O(k)。但是它也有一个问题，那就是卷积操作的时候是O(N^2)，而且必须要对U进行特征值分解，如果一个图是几万个节点的话，这无疑是操蛋的。
现在要解决上图中的问题三，ChebNet是利用Chebyshev polynomil来解决的：
这是一个递归的东西，现在用去代替上图的x，那么：
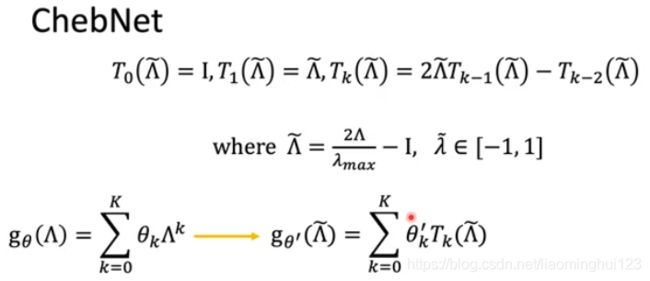如上图所示，我们求解的问题就转化为另外一个了，而且后一个更易于求解，上图where后面的变换是为了把值压在[-1,1]以适用于Chebyshev polynomil。
所以现在我们的问题求解就变成了：
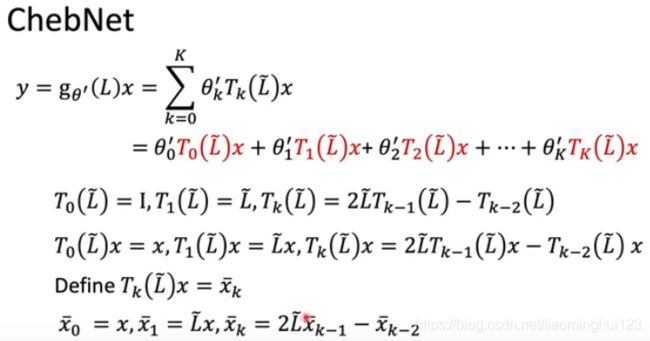进一步将计算成：
在中，右边是可学习的参数，左边有：
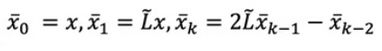而且我们用递归，将最后的复杂度降到O(KE)。
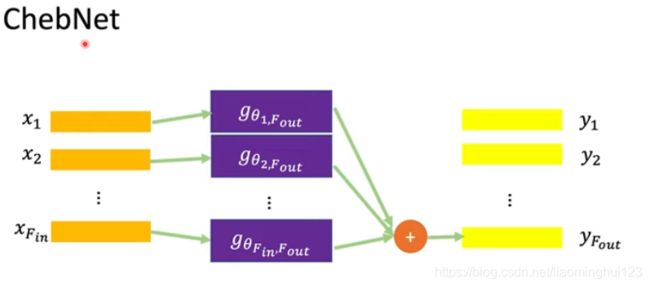
类似于CNN的多通道，这里也可以搞个多通道：

GCN

上图是GCN的传播的推导（GCN就是K=1），红之所以可以这样命令是因为我们的函数是任意的可以随便搞。以上用了对称归一化。
最后：
上图的第二个式子告诉我们在GCN中：你要更新一个节点 的信号（特征向量）的话，你要做的事情就是把它所有的邻接点包括它自己的特征经过一个转换（乘以W）然后全部加起来再取平均，再加上一个bias，最后取一个非线性激活函数就是了。 （编者按：加粗字体是作者自己讲的，可是它的邻接点在变啊？那咋么会有固定shape的W呢？所以虽然本质上是这个式子，但是不能直接这样做，要在谱域上做）

benchmark

图分类：
一张图片用制造super Pixel表示，然后一个graph去分类:
预测分子溶解度：
节点分类：
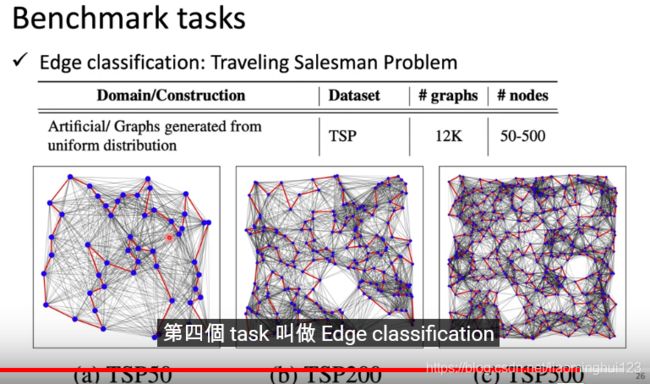
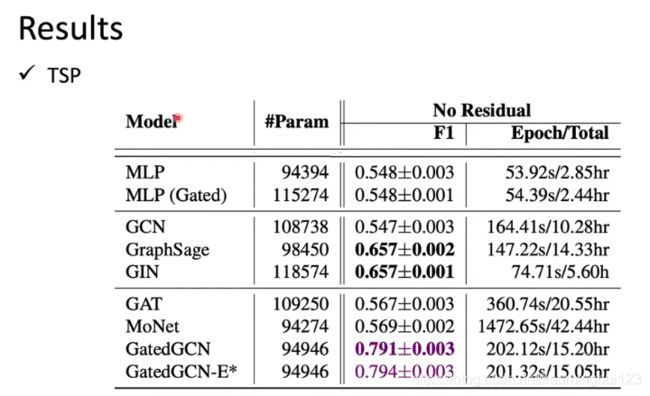
边分类，旅行商问题，边是不是最佳解：

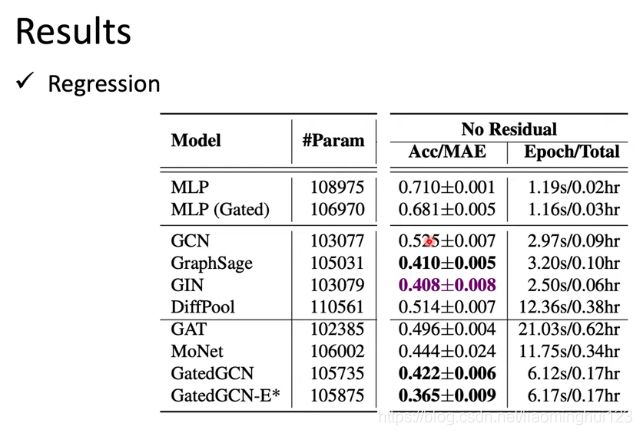
Result

GatedGCN相当于GAT加上GCN, 就是给了权重，效果好；原始GCN跟坨屎一样：
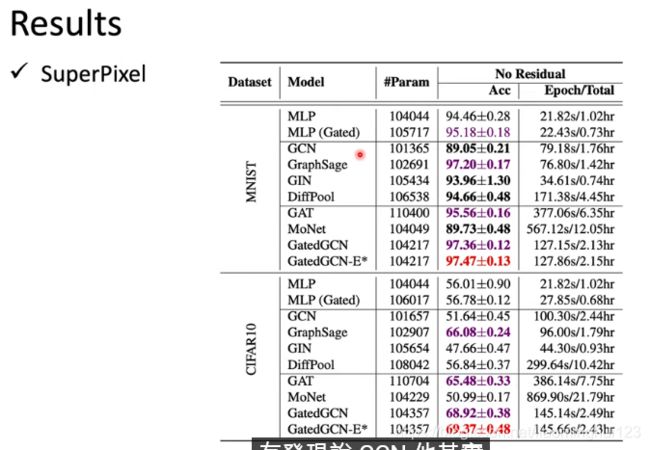GatedGCN相当于GAT加上GCN, 就是给了权重，效果好；原始GCN跟坨屎一样：

补充：GCN在堆层数的时候，会过平滑，可以把一些边给偶然dropout掉。

生成模型:

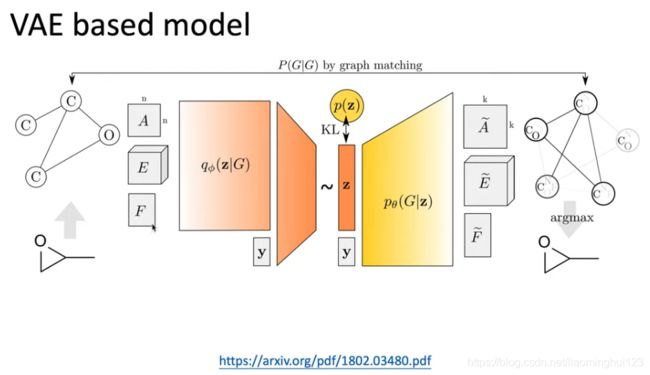
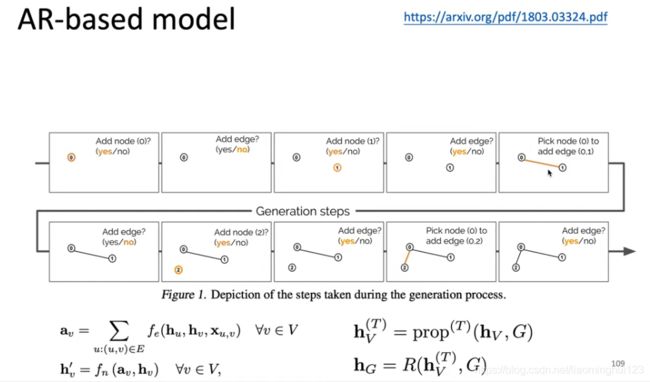
GNN在NLP上面还有应用。
还有一个知识，超图：HyperGCN
GAT和GCN是常见GNN的应用。

上图中GraphBert效果没那么好。

参考文献

本文理解基于台湾大学李宏毅的助教姜成翰同学的GNN课程讲解。
YouTube视频链接