【神经网络+数学】——（2）神经网络求解一元微分问题（一阶微分）

背景

神经网络快速发展，且其具有自动微分的天然功能特性，可以用其来近似逼近待求解函数，利用自动微分来逼近一阶微分，利用自动微分的微分来逼近二阶微分，代入原等式中计算loss，优化后即可得到结果。（以下参考博客）微分方程是由函数以及其导数组成的等式，一般而言，可以分为常微分方程(ODE)和偏微分方程(PDE)，常微分方程按照最高阶导数的阶数可以分为一阶，二阶甚至更高阶，按照函数及其导数的次数又可分为线性微分方程和非线性微分方程。求解微分方程一般有分离变量法和常数变易法等，但是这些方法可以求解的微分方程非常有限，对于更复杂的微分方程，求解解析解几乎是不可能的，于是在实际应用一般采用近似解法。近似解法一般采用离散化的手段，化微分为差分计算。

具体操作取δx=1，一阶差商，理论支撑是泰勒展开

问题举例

以参考博客提到的论文中的一元微分方程为例进行求解。
解析解：

def psy_analytic(x):
    '''
        Analytical solution of current problem
    '''
    return (np.exp((-x ** 2) / 2.)) / (1. + x + x ** 3) + x ** 2

模型代码

使用tf2+python3.7环境，自动微分的结果表示微分函数值，训练代码如下（不包含net类的定义代码，需要付费获取，请私信联系博主）：

# 随机打乱
np.random.seed(2021)
np.random.shuffle(x_space)
y_space = psy_analytic(x_space)
x_space = tf.reshape(x_space, (-1,1))
x_space = tf.cast(x_space, tf.float32)#默认是float64会报错不匹配，所以要转类型
net = SolveNet(x_space, tf.reduce_min(x_space), tf.reduce_max(x_space),w=w,activation=activation)
if retrain:
    net.model_load()
optimizer = Adam(lr)
for epoch in range(epochs):
    grad, loss,loss_data,loss_equation = net.train_step()
    optimizer.apply_gradients(zip(grad, net.trainable_variables))

    if epoch % 100 == 0:
        print("loss:{}\tloss_data:{}\tloss_equation:{}\tepoch:{}".format(loss, loss_data,loss_equation, epoch))
net.model_save()
predict = net.net_call(x_space)
plt.plot(x_space,y_space,'o',label="True")
plt.plot(x_space,predict,'x',label="Pred")
plt.legend(loc=1)
plt.title("predictions")
plt.show()

拟合效果一般，训练收敛很慢，调整了点数、lr、迭代次数、loss权值、激活函数、模型结构等均改变不了收敛慢的问题。
训练日志：

loss:11.477972030639648	loss_data:0.8164212703704834	loss_equation:10.661550521850586	epoch:0
loss:1.4320040941238403	loss_data:0.8163880705833435	loss_equation:0.6156160235404968	epoch:100
loss:1.431862473487854	loss_data:0.816315770149231	loss_equation:0.615546703338623	epoch:200
loss:1.4316843748092651	loss_data:0.8161567449569702	loss_equation:0.6155276298522949	epoch:300
loss:1.4311025142669678	loss_data:0.8156390190124512	loss_equation:0.6154634356498718	epoch:400
loss:1.4280999898910522	loss_data:0.8130143880844116	loss_equation:0.6150856018066406	epoch:500
loss:1.3621699810028076	loss_data:0.7576843500137329	loss_equation:0.6044855713844299	epoch:600
loss:0.16882848739624023	loss_data:0.11115887016057968	loss_equation:0.05766961723566055	epoch:700
loss:0.15744301676750183	loss_data:0.08916334807872772	loss_equation:0.0682796761393547	epoch:800
loss:0.15613119304180145	loss_data:0.08341312408447266	loss_equation:0.0727180689573288	epoch:900
loss:0.15602485835552216	loss_data:0.08219593018293381	loss_equation:0.07382892817258835	epoch:1000
loss:0.15599454939365387	loss_data:0.08199839293956757	loss_equation:0.0739961564540863	epoch:1100
loss:0.1559922695159912	loss_data:0.08243318647146225	loss_equation:0.07355908304452896	epoch:1200
loss:0.15596121549606323	loss_data:0.08180060237646103	loss_equation:0.0741606205701828	epoch:1300
loss:0.1559671312570572	loss_data:0.08122249692678452	loss_equation:0.07474463433027267	epoch:1400
loss:0.15593990683555603	loss_data:0.08169418573379517	loss_equation:0.07424572110176086	epoch:1500
loss:0.1559320092201233	loss_data:0.08180972188711166	loss_equation:0.07412227988243103	epoch:1600
loss:0.15592390298843384	loss_data:0.0816134363412857	loss_equation:0.07431046664714813	epoch:1700
loss:0.1559237390756607	loss_data:0.08191853761672974	loss_equation:0.07400520145893097	epoch:1800
loss:0.15591096878051758	loss_data:0.0815499871969223	loss_equation:0.07436098158359528	epoch:1900
loss:0.15592509508132935	loss_data:0.08212871849536896	loss_equation:0.07379636913537979	epoch:2000
loss:0.15590018033981323	loss_data:0.08148117363452911	loss_equation:0.07441901415586472	epoch:2100
loss:0.1558997929096222	loss_data:0.08172105997800827	loss_equation:0.07417874038219452	epoch:2200
loss:0.1558910757303238	loss_data:0.08143483102321625	loss_equation:0.07445624470710754	epoch:2300
loss:0.15594559907913208	loss_data:0.08212681114673615	loss_equation:0.07381878793239594	epoch:2400
loss:0.15588334202766418	loss_data:0.08139804750680923	loss_equation:0.07448529452085495	epoch:2500
loss:0.15588022768497467	loss_data:0.08129928261041641	loss_equation:0.07458094507455826	epoch:2600
loss:0.15587690472602844	loss_data:0.08130872994661331	loss_equation:0.07456818222999573	epoch:2700
loss:0.1558740884065628	loss_data:0.0813220962882042	loss_equation:0.07455199211835861	epoch:2800
loss:0.1558736115694046	loss_data:0.08114534616470337	loss_equation:0.07472826540470123	epoch:2900
loss:0.15586933493614197	loss_data:0.08129007369279861	loss_equation:0.07457926124334335	epoch:3000
loss:0.15599462389945984	loss_data:0.07986566424369812	loss_equation:0.07612896710634232	epoch:3100
loss:0.15586556494235992	loss_data:0.08127015084028244	loss_equation:0.07459541410207748	epoch:3200
loss:0.15586432814598083	loss_data:0.08119815587997437	loss_equation:0.07466616481542587	epoch:3300
loss:0.15586310625076294	loss_data:0.08131945878267288	loss_equation:0.07454365491867065	epoch:3400
loss:0.15586161613464355	loss_data:0.08123404532670975	loss_equation:0.0746275782585144	epoch:3500
loss:0.1558609902858734	loss_data:0.08126533776521683	loss_equation:0.07459565997123718	epoch:3600
loss:0.15585988759994507	loss_data:0.08121942728757858	loss_equation:0.07464046776294708	epoch:3700
loss:0.15766054391860962	loss_data:0.07656686007976532	loss_equation:0.0810936763882637	epoch:3800
loss:0.15585871040821075	loss_data:0.08118347823619843	loss_equation:0.07467523217201233	epoch:3900
loss:0.15585821866989136	loss_data:0.08119785040616989	loss_equation:0.07466036081314087	epoch:4000
loss:0.15586206316947937	loss_data:0.08086533844470978	loss_equation:0.074996717274189	epoch:4100
loss:0.15585750341415405	loss_data:0.0811905637383461	loss_equation:0.07466694712638855	epoch:4200
loss:0.15585726499557495	loss_data:0.08118582516908646	loss_equation:0.07467144727706909	epoch:4300
loss:0.15585708618164062	loss_data:0.08118223398923874	loss_equation:0.07467484474182129	epoch:4400
loss:0.15585696697235107	loss_data:0.08119025826454163	loss_equation:0.07466670125722885	epoch:4500
loss:0.15585681796073914	loss_data:0.08115758746862411	loss_equation:0.07469922304153442	epoch:4600
loss:0.1558566689491272	loss_data:0.08117453753948212	loss_equation:0.07468213886022568	epoch:4700
loss:0.15585659444332123	loss_data:0.08117266744375229	loss_equation:0.07468392699956894	epoch:4800
loss:0.15825489163398743	loss_data:0.07636100053787231	loss_equation:0.08189389109611511	epoch:4900
model saved in  net.weights

Process finished with exit code 0

loss开始下降快，后面就不动了，但网络并没有收敛完。可能需要更大量的epoch。

将epoch增大为5w，降低lr=0.0001后：

最后的日志：

loss:0.18491655588150024	loss_data:0.0971045270562172	loss_equation:0.08781202137470245	epoch:49400
loss:0.18491658568382263	loss_data:0.09710405766963959	loss_equation:0.08781252801418304	epoch:49500
loss:0.18491649627685547	loss_data:0.09710432589054108	loss_equation:0.0878121629357338	epoch:49600
loss:0.18491670489311218	loss_data:0.09707428514957428	loss_equation:0.0878424271941185	epoch:49700
loss:0.18491661548614502	loss_data:0.09710455685853958	loss_equation:0.08781205117702484	epoch:49800
loss:0.18491646647453308	loss_data:0.09710440784692764	loss_equation:0.08781205862760544	epoch:49900

可见epoch增大后也收敛不动，可能需要加大0~0.4的采样点比重。
增大采样比重后以及尝试了将定义域就缩小到0~0.4仍不行：

欢迎专家学者们前来指导问题的解决方法 ~
加入边界条件：

border condition: ( 0 1.0 ) ( 1 1.2021768865708777 )

加入(0,1)左边界后训练的结果：

加入左右边界后：

效果有了改善，但0~0.4部分的数据点还是拟合较难，最后loss稳定在0.33.且两种loss的数值接近，符合权值设定的比值1:1。

loss:0.33553963899612427	loss_data:0.16740146279335022	loss_equation:0.16813817620277405	epoch:9400
loss:0.3367563784122467	loss_data:0.1700095236301422	loss_equation:0.1667468547821045	epoch:9500
loss:0.3355373740196228	loss_data:0.16735374927520752	loss_equation:0.1681836098432541	epoch:9600
loss:0.3377203941345215	loss_data:0.1711915284395218	loss_equation:0.1665288805961609	epoch:9700
loss:0.3355345129966736	loss_data:0.16736479103565216	loss_equation:0.16816972196102142	epoch:9800
loss:0.3443479537963867	loss_data:0.1772960126399994	loss_equation:0.16705194115638733	epoch:9900

根据实际的拟合效果，data loss的权重增大，训练参数设置为：

activation='tanh'
grid = 10
epochs = 10000
lr = 0.001#第一次训练为0.01 后续训练设置为0.001
w = (2,1)#增大data loss的比重，提高拟合能力

训练后效果改善：

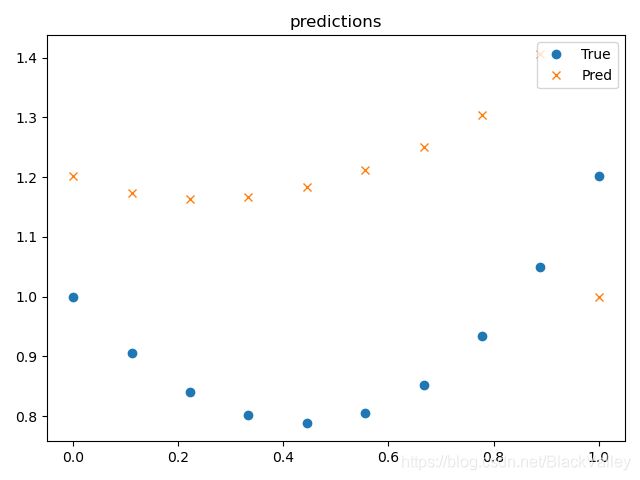
反复训练，并在训练至loss稳定后恢复w=(1,1)继续训练至loss稳定：

loss:0.28020137548446655	loss_data:0.13968469202518463	loss_equation:0.14051669836044312	epoch:9700
loss:0.27985408902168274	loss_data:0.1399995982646942	loss_equation:0.13985449075698853	epoch:9800
loss:0.27987027168273926	loss_data:0.13984116911888123	loss_equation:0.14002911746501923	epoch:9900

可见loss有所下降，从0.33的极限降低到了0.27.虽然有一定的效果，但拟合效果仍达不到预期。
最后经过排查，是粗心的问题，对边界值A和B参数的计算写反了，修正后效果正常：

但问题是如何调整超参loss均不下降，只是微微波动，所以导致拟合效果无法进一步增强，同时w=(4,1)仍无效，lr从0.1到0.0001时loss均不为所动。
进一步实验，将w = (1,4)后loss继续下降，可见增大equation loss的比重可以提高拟合程度：

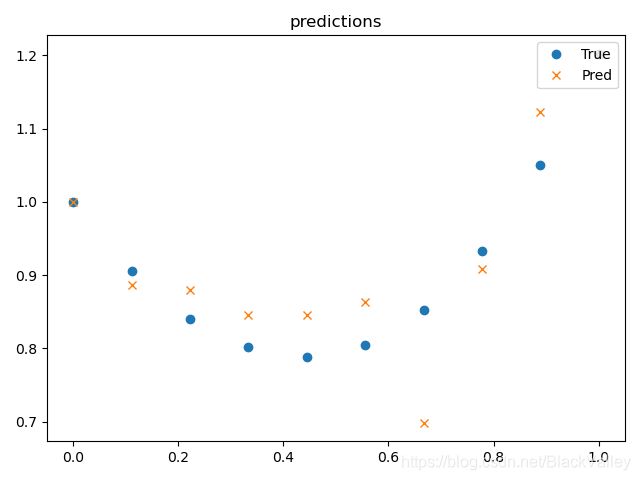
结论

使用自动微分功能可以实现微分方程解析解的模拟近似逼近，但收敛速度较慢，有待优化改进。

参考

CSDN博客