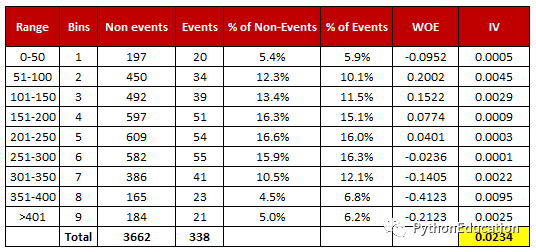
证据权重 (WOE) 与信息价值 (IV)

在本文中，我们将介绍证据权重和信息价值的概念，以及如何在预测建模过程中使用它们，以及如何使用 SAS、R 和 Python 计算它们的详细信息。

逻辑回归模型是解决二分类问题最常用的统计技术之一。这是几乎所有领域都可以接受的技术。这两个概念——证据权重 (WOE) 和信息价值 (IV) 从相同的逻辑回归技术演变而来。这两个术语在信用评分领域已经存在超过 4-5 年了。它们已被用作筛选信用风险建模项目中的变量（例如违约概率）的基准。它们有助于探索数据和筛选变量。它还用于营销分析项目，例如客户流失模型、活动响应模型等。

---

什么是证据权重 (WOE)？

证据权重表明自变量相对于因变量的预测能力。由于它是从信用评分世界演变而来的，它通常被描述为区分好客户和坏客户的衡量标准。“坏客户”是指拖欠贷款的客户。和“优质客户”指的是谁偿还贷款的客户。

商品分布 -特定组中好客户的百分比 不良
分布 -特定组中不良客户的百分比
ln -自然对数

正 WOE 表示货物分布 > 不良品分布
负 WOE 表示商品分布 < 不良品分布

提示：数字的对数 > 1 表示正值。如果小于 1，则表示负值。

许多人不理解商品/不良品这两个术语，因为它们的背景与信用风险不同。从事件和非事件的角度理解 WOE 的概念是很好的。它的计算方法是取非事件百分比和事件百分比除以的自然对数（以 e 为底的对数）。

WOE = In（非事件百分比 ➗ 事件百分比）

计算 WOE 的步骤

1. 对于连续变量，将数据分成 10 份（或更少，具体取决于分布）。

2. 计算每组中事件和非事件的数量（bin）

3. 计算每组中事件的百分比和非事件的百分比。

4. 通过取非事件百分比和事件百分比的自然对数来计算 WOE

注意：对于分类变量，您不需要拆分数据（忽略步骤 1 并按照其余步骤进行操作）

证据权重和信息价值计算

下载：WOE和IV的Excel模板

与 WOE 相关的术语

1. 精细分类

为连续自变量创建 10/20 个 bins/groups，然后计算变量的 WOE 和 IV

2. 粗分类

合并具有相似 WOE 分数的相邻类别

WOE的使用

证据权重 (WOE) 有助于根据因变量分布的相似性（即事件和非事件的数量）将连续自变量转换为一组组或箱。

对于连续自变量：首先，为连续自变量创建分箱（类别/组），然后将具有相似 WOE 值的类别组合起来，并用 WOE 值替换类别。在模型中使用 WOE 值而不是输入值。

数据年龄1；
设定年龄；
如果年龄=。那么 WOE_age = 0.34615;
如果年龄 >= 10 那么 WOE_age = -0.03012;
如果年龄 >= 20 那么 WOE_age = 0.07689;
运行;

proc 逻辑数据=age1 降序；
模型 y = WOE_age;

运行;

对于分类自变量：组合具有相似 WOE 的类别，然后创建具有连续 WOE 值的自变量的新类别。换句话说，在模型中使用 WOE 值而不是原始类别。转换后的变量将是具有 WOE 值的连续变量。它与任何连续变量相同。

为什么将具有相似 WOE 的类别组合在一起？

这是因为具有相似 WOE 的类别具有几乎相同的事件和非事件比例。换句话说，这两个类别的行为是相同的。

WOE相关规则

1. 每个类别 (bin) 应至少有 5% 的观察值。

2. 对于非事件和事件，每个类别 (bin) 都应该是非零的。

3. 每个类别的 WOE 应该是不同的。类似的群体应该被聚合。

4. WOE 应该是单调的，即随着分组增加或减少。

5. 缺失值单独装箱。

箱数（组）

一般来说，取 10 或 20 个 bin。理想情况下，每个 bin 应包含至少 5% 的案例。bin 的数量决定了平滑的数量 - bin 越少，平滑越多。如果有人问你“为什么不形成 1000 个垃圾箱？” 答案是捕获数据中重要模式的 bin 越少，同时排除噪声。案例少于 5% 的 bin 可能不是数据分布的真实情况，并可能导致模型不稳定。
 

处理零事件/非事件

如果特定 bin 不包含事件或非事件，您可以使用以下公式忽略丢失的 WOE。我们将组中事件和非事件的数量增加 0.5。

调整后的WOE = ln（（（组中的非事件数+ 0.5）/非事件数））/（（组中的事件数+ 0.5）/事件数））

如何使用 WOE 检查正确的分箱

1. WOE 应该是单调的，即随着 bin 增加或减少。您可以在图表上绘制 WOE 值并检查线性度。
2.分箱后进行WOE变换。接下来，我们使用 1 个具有 WOE 值的自变量运行逻辑回归。如果斜率不是 1 或截距不是ln（非事件的百分比/事件的百分比），则分箱算法不好。[来源： 文章]

WOE 的好处

1. 它可以处理异常值。假设你有一个连续变量，比如年薪，极值超过5亿美元。这些值将被归为一类（假设为 250-5 亿美元）。稍后，我们将使用每个类别的 WOE 分数，而不是使用原始值。

2. 它可以处理缺失值，因为缺失值可以单独装箱。

3. 由于 WOE 转换处理分类变量，因此不需要虚拟变量。

4. WoE 转换可帮助您与对数赔率建立严格的线性关系。否则用对数、平方根等其他变换方法很难实现线性关系。总之，如果你不使用WOE变换，你可能需要尝试几种变换方法来实现这一点。

什么是信息价值 (IV)？

信息值是在预测模型中选择重要变量的最有用的技术之一。它有助于根据变量的重要性对变量进行排名。IV 使用以下公式计算：

IV = ∑（非事件百分比 - 事件百分比）* WOE

信息价值相关规则

                                                             

信息价值	可变预测性
小于 0.02	对预测没有用
0.02 到 0.1	预测能力弱
0.1 到 0.3	中等预测能力
0.3 到 0.5	强大的预测能力
>0.5	可疑的预测能力

根据 Siddiqi (2006)，按照惯例，信用评分中 IV 统计量的值可以解释如下。

如果 IV 统计量是：

1. 小于 0.02，则预测器对建模没有用

2. 0.02 到 0.1，则预测变量与 Goods/Bads 优势比的关系很弱

3. 0.1 到 0.3，则预测变量与 Goods/Bads 优势比具有中等强度关系

4. 0.3 到 0.5，则预测变量与 Goods/Bads 优势比有很强的关系。

5. > 0.5，高的可疑（需要检查）

要点

1. 信息值随着自变量的 bins/groups 增加而增加。当有超过 20 个 bin 时要小心，因为有些 bin 可能只有很少的事件和非事件。

2. 当您构建除二元逻辑回归（例如随机森林或 SVM）以外的分类模型时，信息值不是最佳特征（变量）选择方法，因为条件对数几率（我们在逻辑回归模型中预测）高度相关到证据权重的计算。换句话说，它主要是为二元逻辑回归模型设计的。也可以这样想 - 随机森林可以很好地检测非线性关系，因此通过信息值选择变量并在随机森林模型中使用它们可能不会产生最准确和鲁棒的预测模型。

如何计算连续因变量的 WOE 和 IV

连续因变量的 WOE 和 IV

Python、SAS 和 R 中的证据权重和信息价值

• 代码

• Python代码

• SAS代码

第 1 步：安装和加载包首先你需要安装“信息”包，然后你需要在 R 中加载包。

install.packages("信息")
库(信息)

第 2 步：导入您的数据

#读取数据
mydata <- read.csv("https://stats.idre.ucla.edu/stat/data/binary.csv")

第 3 步：汇总数据

在这个数据集中，我们有四个变量和 400 个观察值。变量admit 是一个二元目标或因变量。

摘要（我的数据）

     承认gre gpa排名     
 最小。:0.000 分钟 :220 分钟 :2.26 分钟 :1.00  
 第 1 行：0.000 第 1 行：520 第 1 行：3.13 第 1 行：2.00  
 中位数：0.000 中位数：580 中位数：3.40 中位数：2.00  
 平均值：0.318 平均值：588 平均值：3.39 平均值：2.48  
 第三曲：1.000 第三曲：660 第三曲：3.67 第三曲：3.00  
 最大限度。:1.000 最大 :800 最大 :4.00 最大 :4.00

第 4 步：数据准备
确保您的独立分类变量作为因子存储在 R 中。您可以使用以下方法进行操作 -

mydata$rank <- 因子（mydata$rank）

重要说明：在按照此包运行 IV 和 WOE 之前，二进制因变量必须是数字。不要让它成为因素。

第 5 步：计算信息价值和 WOE

在第一个参数中，您需要定义数据框，然后是目标变量。在 bins= 参数中，您需要指定要为 WOE 和 IV 创建的组数。

IV <- create_infotables(data=mydata, y="admit", bins=10, parallel=FALSE)

它将除因变量之外的所有变量作为数据集中的预测变量，并对它们运行 IV。

该函数支持并行计算。如果你想在并行计算模式下运行你的代码，你可以运行以下代码。

IV <- create_infotables(data=mydata, y="admit", bins=10,    parallel=TRUE )

您可以添加ncore=参数以提及用于并行处理的内核数。

R 中的信息值 在 IV 列表中，列表摘要包含所有自变量的 IV 值。

IV_Value = data.frame(IV$Summary)

要获取变量gre 的WOE 表，您需要从 IV 列表中调用表列表。

打印（IV$Tables$gre，row.names=FALSE）

打印（IV$Tables$gre，row.names=FALSE）
       gre N 百分比 WOE IV
 [220,420] 38 0.0950 -1.3748 0.128
 [440,480] 40 0.1000 -0.0820 0.129
 [500,500] 21 0.0525 -1.4860 0.209
 [520,540] 51 0.1275 0.2440 0.217
 [560,560] 24 0.0600 -0.3333 0.223
 [580,600] 52 0.1300 -0.1376 0.225
 [620,640] 51 0.1275 0.0721 0.226
 [660,660] 24 0.0600 0.7653 0.264
 [680,720] 53 0.1325 0.0150 0.265
 [740,800] 46 0.1150 0.7653 0.339

要将其保存在数据框中，您可以运行以下命令 - gre = data.frame(IV$Tables$gre)

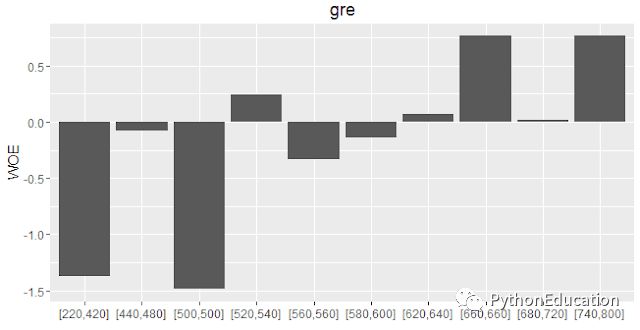
绘制 WOE 分数

要查看 WOE 变量的趋势，您可以使用plot_infotables函数绘制它们。

plot_infotables(IV, "gre")

WOE 情节

要在一页上生成多个图表，您可以运行以下命令 -

plot_infotables(IV, IV$Summary$Variable[1:3], same_scale=FALSE)

多图 WOE

重要点 
是要注意“等级”变量的箱数。由于它是一个分类变量，bin 的数量将取决于因子变量的唯一值。参数 bins=10 不适用于因子变量。

版权声明：文章来自公众号(python风控模型),未经许可，不得抄袭。遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。

欢迎学习csdn学院更多金融风控相关知识《python金融风控评分卡模型和数据分析》